PRML_Exercises
Pattern Recognition and Machine Learning习题中文详解
欢迎讨论题目(我把自己做的过程贴出来也是为了更方便讨论),禁止一切形式的转载。
关于排版,实话说我也想把公式排得舒服好看一些,奈何着实费力,这着实不太讨喜,见谅。
Chapter 1
1.1
能够使得式(1.2)给出的误差函数最小的参数
w={wi}就是使得误差为
0的参数,那么就满足
j=0∑Mwjxnj=tn
而我们要做的这道证明题的右式
Ti=n=1∑N(xn)itn
直接将上述我们已知的
tn代入,得
Ti=n=1∑N[(xn)ij=0∑Mwj(xn)j]
又由于
(xn)i不含有与
j相关的系数,所以可以将其放入后面的求和项,即
Ti=n=1∑Nj=0∑M(xn)iwj(xn)j
再互换一下求和顺序
Ti=j=0∑Mn=1∑N(xn)iwjxnj=j=0∑Mn=1∑N(xn)i+jwj
其中就可以看到
∑n=1N(xn)i+j就是题目中的
Aij了,从而得证。
1.2
已知
E
(w)=21n=1∑N{y(xn,w)−tn}2+2λ∥w∥2
其中
∥w∥2≡wTw=w02+w12+…+wM2,这里提一下正则项里面的
w02,作者说通常来讲这一项要么不放正则项中,要么使用另一个
λ对其进行大小控制,不过咱们这里为了公式的推导方便就不做特殊处理,且让它在这个正则项中。既然题目中要求这个误差函数
E
(w)最小化,也就意味着该式对各个参数
w的导数均为
0,由此可得:
dwidE
(w)=21n=1∑N{2[j=0∑Mwj(xn)j−tn](xn)i}+λwi=0
所以
n=1∑N{j=0∑M[(xn)i+jwj]−(xn)itn]}+λwi=n=1∑Nj=0∑M{(xn)i+jwj}−n=1∑N{(xn)itn+Nλwi}=0
所以可以看到,题目1.1中的式子基本都可以保持不变,只需将
Ti修改为
Ti=∑n=1N{(xn)itn+Nλwi}。
Tips:上面求导的过程使用了复合函数的求导。
1.3
已知
p(B=r)=0.2,
p(B=b)=0.2,
p(B=g)=0.6,同时,
p(F=a∣B=r)=0.3,
p(F=o∣B=r)=0.4,
p(F=l∣B=r)=0.3,
p(F=a∣B=b)=0.5,
p(F=o∣B=b)=0.5,
p(F=l∣B=b)=0,
p(F=a∣B=g)=0.3,
p(F=o∣B=g)=0.3,
p(F=l∣B=g)=0.4。第一小问说,抽一次抽出苹果的概率是多少,可通过sum rule和product rule求出,即:
p(a)=p(a,r)+p(a,b)+p(a,g)=p(a∣r)p(r)+p(a∣b)p(b)+p(a∣g)p(g)=0.34
第二小问说,在已知抽出的结果是橘子(orange)的情况下,从绿色(green)盒子中抽出这个橘子的概率是多大。这就是一个很典型的由果推因的贝叶斯公式题,相当于求
p(B=g∣F=o),根据贝叶斯公式,可得
p(g∣o)=p(o)p(o∣g)p(g),其中分母可以按照第一小问的方式求出,分子中各项均为已知条件,求得
p(B=g∣F=o)=0.5。
1.4
已知
x=g(y),
py(y)=px(x)∣dydx∣=px(x)∣g′(y)∣,对于两个概率分布而言,能够取到最大值的位置满足导数为
0,因此
∂y∂py(y)=∂y∂px(x)∣g′(y)∣=0,题目中假设
x=g(y)为线性函数,因此我们假设
x=g(y)=ay+b,所以可以得到
∂y∂py(y)=∂x∂px(x)∣a∣∂y∂x=∂x∂px(x)∣a∣2=0,由于
∣a∣2>0,(
a的绝对值不应该为
0,否则并不能称其为变换了),所以使得
∂x∂px(x)=0的情况下,
∂y∂py(y)也等于
0,也就是说在
x取值使得
px(x)最大的位置,这个
x对应的
y也是使得
py(y)最大的位置,而
x=g(y)=ay+b同样满足两变量之间的线性关系。
1.5
式(1.38)为
var[f]=E[(f(x)−E[f(x)])2],因此
var[f]=E[(f(x)−E[f(x)])2]=E[f(x)2−2f(x)E[f(x)]+(E[f(x)])2],所以
var[f]=E[f(x)2]−2(E[f(x)])2+(E[f(x)])2]=E[f(x)2]−E[f(x)]2。
1.6
根据式(1.41)可知,
cov[x,y]=Ex,y[xy]−E[x]E[y]。设变量
x,
y独立同分布,对应的分布分别为
p(x)与
p(y),则
Ex,y[xy]=∬xyp(xy)dxdy=∬xyp(x)p(y)dxdy=∫yq(y)∫xp(x)dxdy,由于第二个积分与第一个积分项无关(相互独立,两者之间没有函数关系),因此可以拎出来,得
Ex,y[xy]=∫xp(x)dx∫yq(y)dy=E[x]E[y],所以在两变量互相独立的情况下,
cov[x,y]=Ex,y[xy]−E[x]E[y]=0。
1.7
令
x=rcosθ,
y=rsinθ,满足
x2+y2=r2且
r≥0,则原来的积分式可以写成
I2=∫−∞∞∫−∞∞exp(−2σ21x2−2σ21y2)dxdy=∫o2π∫0∞exp(−2σ21r2)rdrdθ,使用
u=r2代换,
所以
I2=21∫o2π∫0∞exp(−2σ21u)dudθ=21∫02π(−2σ2)exp(−2σ21u)∣0∞dθ=2πσ2,所以
I=(2πσ2)1/2。
1.8
式(1.46)为
N(x∣μ,σ2)=(2πσ2)1/21exp{−2σ21(x−μ)2}=p(x−μ),即要证明
∫−∞+∞x(2πσ2)1/21exp{−2σ21(x−μ)2}dx=∫−∞∞xp(x−μ)dx=μ。先抛开该式不谈,我们需要换元,且必须手头拿到一个已知的东西,那么我们首先有
∫−∞+∞(x−μ)(2πσ2)1/21exp{−2σ21(x−μ)2}d(x−μ)=0,这个比较简单,根据奇函数积分为
0可得,然后我们把这个式子在
(x−μ)这里展开,可以看到即
∫−∞∞xp(x−μ)d(x−μ)−μ∫−∞∞p(x−μ)d(x−μ)=∫−∞∞xp(x−μ)dx−μ=0,所以
∫−∞∞xp(x−μ)dx=μ,亦即
E[x]=∫−∞∞N(x∣μ,σ2)xdx=μ。
第二小问要求验证式(1.50)的正确性。在题目1.7中我们得到
∫−∞∞exp(−2σ21(x−μ)2)dx=(2πσ2)1/2,在等式两边对
σ2求导可得
∫−∞∞exp{−2σ2(x−μ)2}(2σ2)22(x−μ)2dx=(2πσ)1/2π,将式子整理后为:
∫−∞∞(2πσ2)1/21exp{−2σ2(x−μ)2}(x−μ)2dx=σ2=E[(x−μ)2],又因为
E[(x−μ)2]=E[x2−2μx+μ2]=E[x2]−2μE[x]+μ2,而我们在上一小问已经知道
E[x]=μ,所以全部带进去可得,
σ2=E[x2]−μ2,所以
E[x2]=σ2+μ2,从而证得式(1.50)。这样一来,式(1.51)也就顺理成章地成立了。
1.9
单元高斯分布的极大值可以通过对其概率分布函数求导得到极值对应的坐标
x=μ,不做赘述。
多元高斯分布函数为
N(x∣μ,Σ)=(2π)D/21∣Σ∣1/21exp{−21(x−μ)TΣ−1(x−μ)},同样进行求导,这里要用到矩阵的求导法则,得
∂x∂N(x∣μ,Σ)=−21N(x∣μ,Σ)∇x{(x−μ)TΣ−1(x−μ)}=−21N(x∣μ,Σ)∇x−μ{(x−μ)TΣ−1(x−μ)},利用PRML(C.19)和(C.20)公式,令
A=(x−μ)TΣ−1,
B=x−μ,则很容易得到
∂x∂N(x∣μ,Σ)=−N(x∣μ,Σ)Σ−1(x−μ),在推导过程中需要注意的是
Σ−1(x−μ)=(x−μ)TΣ−1,这是由于
x−μ是向量所导致的。那么根据求得的导数,同样在
x=μ时取得极值。
1.10
E[x+z]=∬(x+z)p(x,z)dxdz=∬(x+z)p(x)p(z)dxdz=∬xp(x)p(z)dxdz+∬zp(z)p(x)dxdz
对于右侧的式子,由于
x与
z相互独立,
p(z)的积分为1,因此第一项即为
∫xp(x)dx=E[x],同理第二项为
E[z],所以
E[x+z]=E[x]+E[z]。
var[x+z]=E[(x+z)2]−(E[x+z])2,代入第一小问的结果,得到所求方差为
E[x2+z2+2xz]−(E[x]+E[x])2=E[x2]+E[z2]+2E[xz]−(E[x])2−(E[z])2−2E[x]E[z],
又根据题目1.6的结论,化简得到
var[x+z]=E[x2]+E[z2]−(E[x])2−(E[z])2=var[x]+var[z]。
1.11
令
y=lnp(x∣μ,σ2)=−2σ21∑n=1N(xn−μ)2−2Nlnσ2−2Nln(2π),可以得到
∂μ∂y=−σ21∑n=1N(μ−xn)=0,所以
∑n=1N(μ−xn)=0,所以
∑n=1Nμ−∑n=1Nxn=Nμ−∑n=1Nxn=0,所以
μML=N1∑n=1Nxn。
∂σ2∂y=−(2σ2)22∑n=1N(xn−μML)2−2σ2N=0,很容易得到
σML2=N1∑n=1N(xn−μML)2。
1.12
这题其实第一小问挺迷的,主要问题在于为什么作者要使用不同的下标来表示是否独立,或者说,如果作者你想表达这个意思,那你就应该明说啊我透。这样子一来就比较简单明了了,若
n=m,则
E[xn2]根据式(1.50)很容易得到
E[xn2]=μ2+σ2,下标为
m时相同。若
n̸=m,那么按照作者的意思,就是说这俩变量相互独立,所以
E[xnxm]=E[xn]E[xm]=μ2。
其实作者是想用第一小问作为引子来帮助我们证明式(1.57)和式(1.58),那么实际上我是觉得没必要这么麻烦,我们直接证明这两个式子即可,无需绕他给的这条弯路。
对于第一个式子,求取最大似然分布的均值的期望,我们这里假设总共取了
K次数据,每一次都取
N个数据来进行极大似然估计,
xkn表示第
k次取的第
n个数据,那么
E[μML]=K1∑k=1K[N1∑n=1Nxkn]=KN1∑k=1K∑n=1Nxkn,到这里,我们先停一下,假设我们每次取的数据有限,也就是
N有限,但是我们一直取一直取,也就是说
K无限,那么这里就可以看做我对整个分布上所有的
x都取到了,从而推得
xkn的均值就是正态分布
N(x∣μ,σ2)的均值
μ,所以
E[μML]=μ,这就证明了式(1.57)。
对于式(1.58),首先依旧采取我们之前的取数据规定,同时将方差的计算公式展开,
μkML为第
k次取得的数据的均值,则
E[σML2]=K1∑k=1K[N1∑n=1N(xkn−μkML)2]=K1∑k=1K[N1∑n=1N(xkn2−2xknμkML+μkML2)],这就可以拆分为三项,其中第一项与
xkn2相关,沿用上面的思路,相当于取遍了所有的
xkn,所以
K1∑k=1K[N1∑n=1Nxkn2]=E[x2]=μ2+σ2,后面两项可以写成
K1∑k=1K[−2μkMLN1∑n=1Nxkn]+K1∑k=1K[N1∑n=1N(μkML2)],也就是
K1∑k=1K[−2μkML2]+K1∑k=1K[μkML2]=−K1∑k=1K[μkML2],这就比较明白了,后面两项就是
−E[μML2],因此
E[σML2]=μ2+σ2−E[μML2],所以我们就要求这个
E[μML2],这个表达式的含义就是每一次取得的数据的均值的平方的平均值(期望),那么就有
E[μML2]=σμML2+(E[μML])2,根据公式(1.57),我们进一步得到
E[μML2]=σμML2+μ2,所以
E[σML2]=μ2+σ2−E[μML2]=σ2−σμML2,所以任务又进一步变为求这个
σμML2=var[μML],而
var[μML]=var[N1∑n=1Nxn]=N21∑n=1Nvar[xn]=N21∑n=1Nσ2=Nσ2。
所以就有
E[σML2]=μ2+σ2−E[μML2]=σ2−Nσ2=NN−1σ2。
PS:我用MATLAB做了一下实验,与理论完全相符,式(1.57)和式(1.58)实际上也可以从直观上进行理解,这里就不详细说了。
1.13
根据题目(1.12)的推导,这题就很简单了,将
E[μML2]代换为
E[μ2]=μ2即可,那很显然
E[σML2]=μ2+σ2−μ2=σ2。此时,方差的期望也就是无偏的了。
1.14
如果可以写成题目要求的形式(设原矩阵为
W,要写成
W=S+A),那首先可以很容易推断出
A的对角线上的元素都是
0,所以
S对角线上的元素就是
W对角线上的元素。接着就是要证明
S和
A的其余元素也是可解出来的,因为
wij=wijS+wijA,同时
wji=wjiS+wjiA=wijS−wijA,这就可以得到构成一个二元一次方程组,由于参数对应的矩阵的秩为
2,因此方程组必然有解,所以可以写成题目要求的形式。
∑i=1D∑j=1Dxiwijxj=xTWx=xT(S+A)x=xTSx+xTAx,现在重点关注一下
xTAx这一项,因为
xTAx=∑i=1D∑j=1DxiwijAxj,那么
A的对角线元素皆为
0,同时对称元素互为相反数,(注意,
A和另外两个矩阵都是方阵,这是前提条件),相当于
xiwijAxj+xjwjiAxi=0,所以
xTAx=0,所以
∑i=1D∑j=1Dxiwijxj=xTWx=xTSx+xTAx=xTSx=∑i=1D∑j=1DxiwijSxj。
最后一小问就相当于问我们矩阵
S的对角线以及上(或下)三角部分一共有几个元素,使用数列求和的方式,我们得到
1+2+3+⋯+D=D(D+1)/2,因此独立的元素数量就是这么多。
1.15
根据题目1.14可知,由所有
wi1i2…iM构成的高维张量也是一个高维对称张量,其中的独立元素使用
w~i1i2…iM表示,此时要证明的式子就比较好理解了,由于张量的对称性质,其余元素都是非独立的,因此均可不做考虑,在根据
i1至
iM确定了张量的维度顺序后,假设
i1=1,那么由于剩下的维度中非独立元素所处的维度小于等于第一维的维度,因此
i2的上限是
i1,同理,剩下的和式也是可以推出来的。由此我们可以得到形式为
∑i1=1D∑i2=1i1⋯∑iM=1iM−1w
i1i2⋯iMxi1xi2⋯xiM。
Tips:实际上我还是没有想明白对称的高维张量是长啥样的。
接着要证明
n(D,M)=∑i=1Dn(i,M−1),这个也很简单,就将上面第一问的结果拿来用,最外围的求和就是在
i1从
1取到
D的过程中后方所有项的求和,而
i2到
iM一共有
M−1项,所以得证。这个递推式还是比较直观的。
第三小问归纳法也很直接,
D=1的情况下,
∑i=1D(i−1)!(M−1)!(i+M−2)!=(M−1)!(M−1)!=1=(D−1)!M!(D+M−1)!=(1−1)!M!(1+M−1)!=M!M!,此时等式成立,假设取数字
D时,等式成立,则
∑i=1D(i−1)!(M−1)!(i+M−2)!=(D−1)!M!(D+M−1)!,则取数字
D+1时,
∑i=1D+1(i−1)!(M−1)!(i+M−2)!=∑i=1D[(i−1)!(M−1)!(i+M−2)!]+D!(M−1)!(D+M−1)!=(D−1)!M!(D+M−1)!+D!(M−1)!(D+M−1)!=D!M!(D+M)(D+M−1)!,所以
∑i=1D+1(i−1)!(M−1)!(i+M−2)!=D!M!(D+M)!=(D+1−1)!M!(D+1+M−1)!,说明该式在
D+1时仍旧成立,从而归纳得证。
对于任意
D≥1,取
M=2,则有
n(D,M)=(D−1)!M!(D+M−1)!=(D−1)!2!(D+1)!=2D(D+1),正如我们在题目1.14中得到结果一样。现在假设
M−1时,该式成立,即
n(D,M−1)=(D−1)!(M−1)!(D+M−2)!,而
n(D,M)=∑i=1Dn(i,M−1)=∑i=1D(i−1)!(M−1)!(i+M−2)!,又因为
∑i=1D(i−1)!(M−1)!(i+M−2)!=(D−1)!M!(D+M−1)!,所以
n(D,M)=(D−1)!M!(D+M−1)!,所以在
M时,该式依旧成立,从而归纳得证。
1.16
第一小问很直观,根据式(1.74)可知,
n(D,M)仅表征了第
M阶参数的独立元素个数,现在的
N(D,M)相当于求取所有阶(
0阶到
M阶)的独立参数数量,因此
N(D,M)=∑m=0Mn(D,m)。
第二小问,当
M=0时,
N(D,M)=D!M!(D+M)!=1,这与实际相符,当仅含有
0阶时,由于
x无关,所以实际上就一个常数项,因此参数的数量就是
1。现在假设
M时成立,即
N(D,M)=D!M!(D+M)!,则取
M+1时,
N(D,M+1)=D!M!(D+M)!+n(D,M+1)=D!M!(D+M)!+(D−1)!(M+1)!(D+M)!=D!(M+1)!(M+1)(D+M)!+D(D+M)!=D!(M+1)!(D+M+1)!,这里使用了式(1.137)的结论,从而归纳得证。
第三小问使用了斯特林公式
n!≃nne−n,若
D≫M,则
N(D,M)=D!M!(D+M)!≃D!(D+M)!≃DDe−D(D+M)D+Me−(D+M)≃DD(D+M)D+M≃DDDD+M=DM,同理,若
M≫D,则有
N(D,M)=D!M!(D+M)!≃M!(D+M)!≃MMe−M(D+M)D+Me−(D+M)≃MM(D+M)D+M≃MMMD+M=MD,从而得证。
N(10,3)=10!3!(10+3)!=286,
N(100,3)=100!3!(100+3)!=176851。
1.17
已知
Γ(x)≡∫0∞ux−1e−udu,根据分部积分法,可以得到
Γ(x)=∫0∞−ux−1de−u=−ux−1e−u∣0∞+∫0∞e−udux−1=∫0∞e−udux−1,前半部分的积分为
0不做赘述,简单说明一下就是
x是有限项,而
u取无限大项时,无限大的有限次方除以
e的无限大次方时趋近于
0,你也可以用MATLAB测试一下。而
Γ(x+1)=∫0∞e−udux=∫0∞xe−udux−1=xΓ(x),得证。
Γ(1)=∫0∞e−udu=−e−u∣0∞=1,得证。
若
x为整数,那么
Γ(x+1)=∫0∞e−udux,式子中,微分项
ux的次幂就可以一直取下来,得到
Γ(x+1)=∫0∞e−udux=x!∫0∞e−udu=x!。
1.18
有一个疑问,式(1.142)中,为何就称那一项为
SD的呢?凭什么那一项所代表的的含义就是
D维空间中单位球体的表面积呢?我自己想了一下,但是也只是一个头绪,我们看一下题目1.7中的计算过程,其中有一步是算到了
I2=∫o2π∫0∞exp(−2σ21r2)rdrdθ,为了和本题结合,我们取
σ2=1/2,则有
I2=∫o2π∫0∞exp(−r2)rdrdθ,将这个公式对照题目1.18里面的式(1.142),就可以看到,
SD就是我们算出来的这个双重积分项
∫o2π∫0∞exp(−r2)rdrdθ除以这个积分项内层的积分,简单来说,通过这么一个除法,原本对于整个平面的积分(
r从
0取到
∞),变成了单位长度,同时又消除了
exp(−r2)这一项的积分影响,相当于算了一个在极小角度下的单位半径的扇形的面积,那么再对这个扇形进行角度上的积分,转一圈就得到了单位圆的面积。所以式(1.142)就是这个过程在更高维空间的一个推广。这是我的理解。
首先,根据式(1.126),可以推知,
∏i=1D∫−∞∞e−xi2dxi=πD/2,简单说一下就是,根据式(1.126),我们知道在
D=2的时候,
∏i=12∫−∞∞e−xi2dxi=π,所以就比较明显了。这样子我们就有了左式的值,对于右式,可以转化为
SD∫0∞e−r2rD−1dr=SD21∫0∞e−r2(r2)D/2−1dr2,根据题目1.17,也就可以看出,
SD∫0∞e−r2rD−1dr=SD21Γ(D/2),所以
πD/2=SD21Γ(D/2),所以
SD=Γ(D/2)2πD/2。
同样用简单一点的情况来帮助我们理解复杂的高维情况,比如说我们现在知道一个单位圆的周长,如何得到单位圆的面积呢,已知单位圆周长为
2π,面积就相当于这个单位圆向内放缩后直至变成零点的所有圆的周长积分,同时,还需要了解一个基本事实,那就是在一个
D维空间中,其体积的大小正比于
rD,而表面积则正比于
rD−1。现在我们举的例子是在
2维空间下,因此二维单位圆面积就等于
∫012πr2−1dr=π,这也符合我们已知的先验事实。因此,
VD=∫01SDrD−1dr=SDD1rD∣01=DSD。
D=2时,
SD=2π,
VD=π,
D=3时,
SD=4π,
VD=34π。
多说一点,PRML书中说在高维空间中,球体体积就几乎完全贴近表面分布,其实在
2维单位圆中这种现象就已经初现端倪了,在刚刚给出的求出单位圆面积的积分过程中,很明显越靠近圆心的单位圆,其周长越小,对整个圆的表面积贡献越小,而半径越接近
1的圆其周长越大,对整个圆的表面积贡献就越大,这种效应在高维空间中会表现得更加显著,因为往高维变化的过程中,周长正比于半径的
D−1次方,次幂会加剧这种拉扯。感性理解一下就好。
1.19
半径为
a的
D维超球,体积就是
∫0aSDrD−1dr=SDaD/D,而边长为
2a的
D维超立方体体积很容易求得为
2DaD,因此
volumeofcubevolumeofsphere=D2DSD=D2DΓ(D/2)2πD/2=D2D−1Γ(D/2)πD/2。因此在超高维空间中,单位超球的体积对于包络住这个单位超球的超立方体而言是微不足道的。
第二小问这个直接带进去,很容易看到趋近于
0,不做赘述。
D维空间中,边长为
2a的超立方体的中心到角落的距离为
∑1Da2
=Da2
=D
a,所以其与半径之比就是
D
。如果你要问为什么这么求,其实依然是可以从简单的情况出发的,比如说在三维空间中,你为了求出立方体的中心到角落的距离,就是使用两次勾股定理,相当于进行两次降维,最终到达角落所处的点。如果从线性代数的角度来说的话,就是我们沿着标准基的方向走。还是比较好理解的。
1.20
式(1.148)可以直观得到,在使用
r作为随机变量后,一个随机变量对应的几何形式就是“一周”,例如二维高斯分布中,依题目中均值均为
0,且方差相等的设置,同一
r对应的就是以原点为中心的圆形,因此其对应的概率函数就是“周长”乘以对应的概率值,即
p(r)=(2πσ2)D/2SDrD−1exp(−2σ2r2)。
第二小问
drdp(r)=(2πσ2)D/2(D−1)SDrD−2exp(−2σ2r2)+σ2(2πσ2)D/2−SDrDexp(−2σ2r2)=0,等式两边除以一些共有项,则有
(rD−2)(D−1)=σ2rD,因为
D足够大,因此可以转化为
(rD−2)D≃σ2rD,所以
r^≃D
σ。
已知
p(r)∝rD−1exp(−2σ2r2)=exp{−2σ2r2+(D−1)ln(r)},需要注意,式子中省略了
(2πσ2)D/2SD这一项,在驻点附近,使用泰勒级数展开,以求出
ln(r^+ϵ),所以
p(r^+ϵ)∝exp{−2σ2(r^+ϵ)2+(D−1)ln(r^+ϵ)},而
ln(r^+ϵ)≃ln(r^)+r^1ϵ−2r^21ϵ2,放进去就可以得到
p(r^+ϵ)∝exp{−2σ2(r^+ϵ)2+(D−1)(ln(r^)+r^1ϵ−2r^21ϵ2)}=r^D−1exp(−2σ2(r^+ϵ)2+(D−1)(r^1ϵ−2r^21ϵ2)),在指数项中代入
r^≃D
σ,同时由于
D很大,因此得到
p(r^+ϵ)∝r^D−1exp(−2σ2(r^+ϵ)2+2σ22r^ϵ−ϵ2),也就是
p(r^+ϵ)∝r^D−1exp(−2σ2r^2−2σ22ϵ2),所以
p(r^+ϵ)=p(r^)exp(−σ2ϵ2)。这里我算出来和题目给的不一样,我检查了好几遍,级数展开那边是没有问题的。留待观察吧。
p(∣∣x∣∣=0)=(2πσ2)D/21,
p(∣∣x∣∣=r^)=(2πσ2)D/21exp(−D/2),因此
p(∣∣x∣∣=0)=p(∣∣x∣∣=r^)exp(−D/2)。
1.21
因为
0≤a≤b,所以
a2≤ab,所以
a≤(ab)1/2。
[外链图片转存失败(img-2amJrAcX-1565057031898)(.\curve.jpg)]
这里我按照书中的Figure 1.24绘制了上图,按照最小化误差率进行了分割,那么可以看到,两条概率曲线是有重合的部分的,我设其对应的随机变量取值分别为
K1和
K3,而分割处对应的随机变量为
K2,由式(1.78)可知,
p(mistake)=∫R1p(x,C2)dx+∫R2p(x,C1)dx,那么根据上面这种图片(左峰是
p(x,C1)),我们更加精确地表达这个式子,即
p(mistake)=∫K1K2p(x,C2)dx+∫K2K3p(x,C1)dx=
a,而在随机变量取值
K1至
K3之间的全部面积,其面积大小为
b=∫K1K2p(x,C1)dx+∫K2K3p(x,C2)dx,可以看到
0≤a≤b,因此就有
p(mistake)≤(ab)1/2,积分决定了两项之间是否能够相乘,因此就有
(ab)1/2=∫K1K3{p(x,C1)p(x,C2)}1/2dx,从而得证。
1.22
根据式(1.80)可知,当损失矩阵按照题目的意思设置时,
E[L]=∑k∑j(j̸=k)∫Rjp(x,Ck)dx,此时该式就相当于最小化
p(mistake)因此也就相当于退化为,谁的后验概率大就取谁的值。简单来说就是,这种损失矩阵对于所有的错误判断都一视同仁,权重都是
1,那这时候有没有这个损失矩阵都没差别了。也就变成了前一小节所说的最小化错误分类概率。
1.23
对于某一类,如
Cj,按照式(1.81),就相当于对该类最小化
∑kLkjp(Ck∣x),而
p(Ck∣x)=p(x)p(x∣Ck)p(Ck),所以就要最小化
∑kLkjp(x)p(x∣Ck)p(Ck)。
1.24
这题我刚开始做是比较懵逼的,主要是看不懂题目,太难翻译了有木有。来,我给大家准确梳理一下这道题的意思,分类问题中可以引入损失的权重来计算期望损失,并尽可能最小化该值,先不管什么拒绝选项,那我们可以根据式(1.81)知道,当新来了一个
x的时候,我要做的就是遍历所有的
j,然后看哪个
j带进去的时候,
∑kLkjp(Ck∣x)能取到最小值,而且按照书中的说法,决策论干的这些个事都很简单,毕竟推断的阶段,把那些个求解过程中需要的概率分布都给决策论准备好了。那么现在,我们再引入拒绝选项这个概念,所谓拒绝选项的含义就是,比如说在二分类问题中,就比如上面那张图片,在
K2处,这俩的概率是完全相同的,如果从后验概率的角度来说,就是这俩“五五开”。这种时候,数学也很为难,拒绝选项就可以在这种接近于五五开的情况下做出拒绝判断的选择。而题目中给出的
λ就是在使用期望分类损失之后引入的“损失阈值”,说实话,光看题目我愣是没有抿出
λ是这个意思,看了solution又悟了好久才把作者的整个思路弄明白。那就很简单了,所谓的决策就是,在能够使得
∑kLkjp(Ck∣x)取得最小值的情况下,如果该值还是超过
λ,就拒绝,其他情况就分类为能够使得
∑kLkjp(Ck∣x)最小的那个第
j类。在
Lkj=1−Ikj的情况下,与题目1.22一致,此时所有后验分布一视同仁,不厚此薄彼,根据sum rule,就可以得到
∑kp(Ck∣x)=1−p(Cj∣x),这时候,就是最开始我们接触的没有权重的拒绝选项了。对比Figure 1.26,也很容易得到
λ=1−θ。
1.25
已知
E[L(t,y(x))]=∬∣∣y(x)−t∣∣2p(x,t)dxdt,所以可得
δy(x)δE[L(t,y(x))]=2∫{y(x)−t}p(x,t)dt=0,所以可得
y(x)∫p(x,t)dt=∫tp(x,t)dt。根据sum rule,可推知
y(x)p(x)=∫tp(x,t)dt,所以
y(x)=p(x)∫tp(x,t)dt=∫tp(t∣x)dt=Et[t∣x]。很明显,如果目标量由向量
t变为标量
t,则对应的结果就退化为式(1.89),即
y(x)=Et[t∣x]。
1.26
这道题很简单,依葫芦画瓢即可,那些过程和繁杂的公式我宁可不耗费时间去把它打出来,我有一个疑问,那就是为什么中间的那个交叉项消失了?
先来看式(1.90)的推导过程中的那个式子
{y(x)−t}2={y(x)−E[t∣x]}2+2{y(x)−E[t∣x]}{E[t∣x]−t}+{E[t∣x]−t}2,中间的交叉项在积分过程中即
∬2{y(x)−E[t∣x]}{E[t∣x]−t}p(x,t)dxdt,注意,式子中,
E[t∣x]是
Et[t∣x]的简写,所以
E[t∣x]是关于
x的表达式,中间项的积分即
2∬{y(x)E[t∣x]−y(x)t−(E[t∣x])2+tE[t∣x]}p(x,t)dxdt,这里说白了就是四项之和的双重积分,一项一项来看,忽略掉最前面的系数
2,第一项为
∬y(x)E[t∣x]p(x,t)dxdt=∫y(x)E[t∣x]∫p(x,t)dtdx=∫y(x)E[t∣x]p(x)dx,第二项为
∬−y(x)tp(x,t)dxdt=∫−y(x)p(x)∫tp(x)p(x,t)dtdx=∫−y(x)p(x)E[t∣x]dx,这样一来,第一项和第二项就抵消了,第三项为
∬−(E[t∣x])2p(x,t)dxdt=∫−(E[t∣x])2∫p(x,t)dtdx=∫−(E[t∣x])2p(x)dx,第四项为
∬tE[t∣x]p(x,t)dxdt=∫E[t∣x]p(x)∫tp(x)p(x,t)dtdx=∫(E[t∣x])2p(x)dx,这样一来,第三项和第四项也抵消了,如此即可得到式(1.90)的结果。
本题实际上是一样的推导过程,只是由于变成了向量,在处理时需要注意中间项变为了
(y(x)−E[t∣x])T(E[t∣x]−t)+(E[t∣x]−t)T(y(x)−E[t∣x]),因此最终结果可以写成
E[L]=∫∣∣y(x)−E[t∣x]∣∣2p(x)dx+∫var[t∣x]p(x)dx。
1.27
实话说,看到这题的我也是懵逼的,说起来很简单,就是要保证
E[Lq]可微,且其微分等于
0是有解的。但是问题来了,对谁微分呢?考虑到问题中问的是
y(x)需要满足的条件,而双重积分的微分也是相当棘手,所以最终我还是翻看了solution。作者的意思是既然
y(x)是由我们选择的,同时
p(t,x)正比于
p(t∣x),那么这个双重积分也就可以表达为
∫∣y(x)−t∣qp(t∣x)dt,在这个式子基础上,对
y(x)进行微分,得到
∫q∣y(x)−t∣q−1sign(y(x)−t)p(t∣x)dt=0,本来走到这一步我觉得我勉强能够理解(其实已经很困难了好嘛),作者又一波神奇操作,将其变为
q(∫−∞y(x)∣y(x)−t∣q−1p(t∣x)dt−∫y(x)∞∣y(x)−t∣q−1p(t∣x)dt)=0,所以要满足的条件就是
∫−∞y(x)∣y(x)−t∣q−1p(t∣x)dt=∫y(x)∞∣y(x)−t∣q−1p(t∣x)dt。真的看不大懂每一步操作的理由是什么。
好了我编不下去了,上面几乎就是把solution翻译了一遍,我选择放弃,再想想看。
看了一段时间,稍微有了一些想法,可以看一下式(1.88),我们不妨就从这个角度切入。为什么选择这个角度?因为正是式(1.88)到式(1.89)的推导过程,推出了在
q=2的情况下,条件均值为
y(x)最优解。因此,我们二话不说依葫芦画瓢进行微分(这里使用到了变分法,不做赘述),得到了
δy(x)δE[L]=q∫∣y(x)−t∣q−1sign(y(x)−t)p(x,t)dt=0。那么之所以要使用
y(x)来进行区间的划分,也是为了简化该式的符号项,这才有了
q(∫−∞y(x)(t−y(x))q−1p(t∣x)dt+∫y(x)∞(y(x)−t)q−1p(t∣x)dt)=0,这样符号关系就对了,之后再转换一下正负号,将两部分分别挪至等号两侧,就有了
∫−∞y(x)(y(x)−t)q−1p(t∣x)dt=∫y(x)∞(y(x)−t)q−1p(t∣x)dt。
如果
q=1,则有
y(x)满足
∫−∞y(x)p(t∣x)dt=∫y(x)∞p(t∣x)dt,也就是说
p(t∣x)在
t<y(x)的区域中与
t≥p(t∣x)的区域上积分大小相同,此时
y(x)所在的位置也就是题目所谓的条件中数的含义。
如果
q→0,
∣y(x)−t∣q趋近于
1,这样的话
∫∣y(x)−t∣qp(t∣x)dt也就趋近于
1。但是当
y(x)与
t之间的距离同样非常靠近时,
∣y(x)−t∣q趋近于
1这一点就要打个问号了,这种情况下,
∣y(x)−t∣q会比
1还要小一些(可以使用MATLAB进行验证)。这样一来,能够使得这个“小一些”足够小的
y(x)也就要尽可能靠近出现概率最大的
t值,此时,相当于
y(x)就是条件分布的众数。
1.28
n为正整数为前提条件下,
h(p2)=h(p)+h(p)=2h(p),
h(pn)=h(p)+⋯+h(p)=nh(p)。
m为正整数为前提条件下,
h(pn/m)=nh(p1/m)=mnmh(p1/m)=mnh(p)。这里你可以将
p1/m看成上面公式中的
p,视其为一个整体,因为题中对
p是没有任何要求的。这样一来,就可以看到,对于任何一个正整数
x,
h(px)=xh(p)。
最后一小问没啥意思,不证了。
1.29
H[x]=∑i=1M−p(xi)lnp(xi)=∑i=1Mp(xi)lnp(xi1),
ln函数是一个concave函数,因此
f(∑i=1Mλixi)≥∑i=1Mλif(xi),这里
p(xi)即
λi,满足
λi所需的条件,因此
∑i=1Mp(xi)ln(p(xi)1)≤ln(∑i=1Mp(xi)p(xi)1=lnM)。
所以
H[x]≤lnM。
1.30
在
KL散度的表达中,我一直有一个疑问,就是为什么我们预估的分布
q(x)的信息熵是
−∫p(x)lnq(x)dx,而不是
−∫q(x)lnp(x)dx,最终觉得这是因为按照后者那样去写的话,所谓的编码平均附加信息量这个表达式,也就是
KL散度的数学表达式并不具有良好的数学性质,利用不到convex函数的相关性质。因此才使用了前者那种表达,但是我还想从更加合理的角度来看待这样做的原因。
KL(p∣∣q)=−∫p(x)ln{p(x)q(x)}dx=∫p(x){lnp(x)−lnq(x)}dx=∫p(x){ln(2πσ2)1/21exp(−2σ2(x−μ)2)−ln(2πs2)1/21exp(−2s2(x−m)2)}dx=∫p(x){−ln(2πσ2)1/2−2σ2(x−μ)2+ln(2πs2)1/2+2s2(x−m)2}dx=∫p(x){lnσs}dx−2σ21∫p(x)(x−μ)2dx+2s21∫p(x)(x−m)2dx=lnσs+2s21∫p(x)(x−m)2dx−21=lnσs+2s21∫p(x)(x2−2mx+m2)dx−21=lnσs+2s21(μ2+σ2−2mμ+m2)−21=lnσs+2s2(μ−m)2+σ2−21
1.31
H[x,y]=−∬p(x,y)lnp(x,y)dydx=−∬p(x,y)lnp(y∣x)dydx−∬p(x,y)lnp(x)dydx=−∬p(x,y)lnp(y∣x)dydx−∫lnp(x)∫p(x,y)dydx=H[y∣x]−∫lnp(x)p(x)dx=H[y∣x]+H[x]
H[x]+H[y]=−∫p(x)lnp(x)dx−∫p(y)lnp(y)dy=−∬p(x,y)lnp(x)dydx−∬p(x,y)lnp(y)dydx=−∬p(x,y)lnp(x)p(y)dydx
要证明
H[x,y]≤H[x]+H[y],即变为证明
−∬p(x,y)lnp(x,y)dydx≤−∬p(x,y)lnp(x)p(y)dydx
根据互信息的定义,我们有
I[x,y]=KL(p(x,y)∣∣p(x)p(y))=−∬p(x,y)ln(p(x,y)p(x)p(y))dydx
且
I[x,y]≥0,当且仅当两变量互相独立时等号才成立。所以
−∬p(x,y)ln(p(x,y)p(x)p(y))dydx=−∬p(x,y)ln(p(x)p(y))dydx+∬p(x,y)lnp(x,y)dydx≥0
所以得到
−∬p(x,y)lnp(x,y)dydx≤−∬p(x,y)lnp(x)p(y)dydx
结论成立,且只有在两变量相互独立时等号才成立。
实话说我感觉我这个是伪证明,因为利用了互信息这个先验知识,但是其实也没差,互信息本身就是一种
KL散度,因此必然大于等于
0。看了一眼solution给出的解法,我觉得相当奇怪,既然作者已经利用了互信息这个条件,为什么还整得那么绕?
1.32
非奇异的随机变量线性变换不会改变随机变量的概率密度值,因此
p(Ax)=p(y),同时在概率密度一节中有提及:
p(x)∣δx∣=p(y)∣δy∣,所以有
p(x)=p(y)∣δxδy∣=p(y)∣A∣,所以
H[y]=−∫p(Ax)ln(p(Ax))dx=−∫p(x)ln(p(x)∣A∣−1)dx=−∫p(x)ln(x)dx−∫p(x)ln(∣A∣−1)dx=H[x]+ln(∣A∣)
1.33
已知
H[x,y]=H[y∣x]+H[x]。现在
H[y∣x]=0,所以
H[x,y]=H[x]。因此
−∬p(x,y)lnp(x,y)dydx=−∬p(x,y)lnp(x)dydx
所以
p(x,y)=p(x),又因为
p(x,y)=p(y∣x)p(x),从而得到
p(y∣x)=1,也就是说,在知道了
x的前提条件下,
y是多少一下子就知道了(因为概率为
1,所以说明对于一个固定的
x,就只有一个固定的
y与之对应),也就是说
y与
x之间有着对应的函数关系。这个函数关系并不一定是一一对应的,而只是要求在
x确定了的情况下,只有一个
y与之对应,这是不排除一个相同的
y对应多个不同的
x这种情况的。
1.34
泛函
F为:
−∫−∞∞p(x)lnp(x)dx+λ1(∫−∞∞p(x)dx−1)+λ2(∫−∞∞xp(x)dx−μ)+λ3(∫−∞∞(x−μ)2p(x)dx−σ2)
整理可得:
∫−∞∞{−p(x)lnp(x)+λ1p(x)+λ2xp(x)+λ3(x−μ)2p(x)}dx+{−λ1−λ2μ−λ3σ2)}
令
G=−p(x)lnp(x)+λ1p(x)+λ2xp(x)+λ3(x−μ)2p(x)
则有
dp(x)dG=−lnp(x)−1+λ1+λ2x+λ3(x−μ)2=0
所以
p(x)=exp(−1+λ1+λ2x+λ3(x−μ)2)。
这里参考了Appendix D章节的变分法内容。
1.35
p(x)=(2πσ2)1/21exp{−2σ2(x−μ)2},所以有
H[x]=−∫p(x)lnp(x)dx=−∫(2πσ2)1/21exp{−2σ2(x−μ)2}ln(2πσ2)1/21exp{−2σ2(x−μ)2}dx=∫p(x)(ln((2πσ2)1/2))dx+∫p(x)(2σ2(x−μ)2)dx=21ln(2πσ2)+21=2ln(2πσ2)+1
注意其中有一步是由方差的计算公式得来的。
1.36
根据泰勒展开式,可得
f(x)=f(x0)+f′(x0)(x−x0)+21f′′(x0)(x−x0)2
由于
f′′(x0)>0,因此
21f′′(x0)(x−x0)2>0,所以可得
f(x)>f(x0)+f′(x0)(x−x0)
设
x0=λa+(1−λ)b因此可以得到
f(a)>f(λa+(1−λ)b)+f′(λa+(1−λ)b)((1−λ)(a−b))f(b)>f(λa+(1−λ)b)+f′(λa+(1−λ)b)(λ(b−a))λf(a)+(1−λ)f(b)>f(λa+(1−λ)b)
从而得证。
1.37
H[y∣x]+H[x]=−∬p(x,y)lnp(y∣x)dydx−∫p(x)lnp(x)dx=−∬p(x,y)lnp(y∣x)dydx−∬p(x,y)lnp(x)dydx=−∬p(x,y)ln{p(y∣x)p(x)}dydx=−∬p(x,y)lnp(x,y)dydx=H[x,y]
1.38
当项数为
2时,根据式(1.114)可知
f(λa+(1−λ)b)≤λf(a)+(1−λ)f(b)
现在假设项数为
M时满足
f(i=1∑Mλixi)≤i=1∑Mλif(xi)
当有
M+1项时,则有
f(i=1∑M+1λixi)=f(i=1∑Mλixi+λM+1xM+1)=f((1−λM+1)i=1∑M1−λM+1λixi+λM+1xM+1)≤(1−λM+1)f(i=1∑M1−λM+1λixi)+λM+1f(xM+1)
很明显,
∑i=1M1−λM+1λi=1,因此
f(i=1∑M1−λM+1λixi)≤i=1∑M1−λM+1λif(xi)
所以
f(i=1∑M+1λixi)=f(i=1∑Mλixi+λM+1xM+1)=f((1−λM+1)i=1∑M1−λM+1λixi+λM+1xM+1)≤(1−λM+1)f(i=1∑M1−λM+1λixi)+λM+1f(xM+1)≤(1−λM+1)i=1∑M1−λM+1λif(xi)+λM+1f(xM+1)=i=1∑M+1λif(xi)
由此归纳得证。
1.39
这道题理解了书中的相关公式很好做的,书里面几乎把关系全都明摆出来了。
( a )
ln3−32ln2
( b )
ln3−32ln2
( c )
32ln2
( d )
32ln2
( e )
ln3
( f )
ln3−34ln2
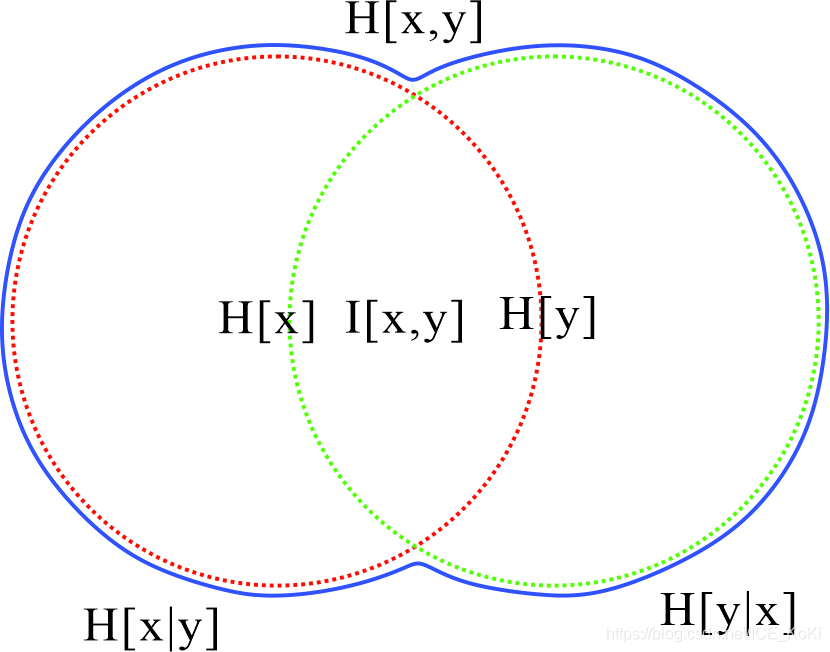
1.40
ln(i=1∑NN1xi)=ln(N1i=1∑Nxi)≤i=1∑NN1lnxi=N1i=1∑Nlnxi=N1lni=1∏Nxi=ln(i=1∏Nxi)N1
由于
ln函数为递增函数,因此
N1i=1∑Nxi≤(i=1∏Nxi)N1
从而得证。
1.41
I[x,y]=KL(p(x,y)∣∣p(x)p(y))=−∬p(x,y)ln(p(x,y)p(x)p(y))dydx=−∬p(x,y)ln(p(y∣x)p(x)p(x)p(y))dydx=−∬p(x,y)ln(p(y∣x)p(y))dydx=H[y]−H[y∣x]=−∬p(x,y)ln(p(x∣y)p(y)p(x)p(y))dydx=−∬p(x,y)ln(p(x∣y)p(x))dydx=H[x]−H[x∣y]

