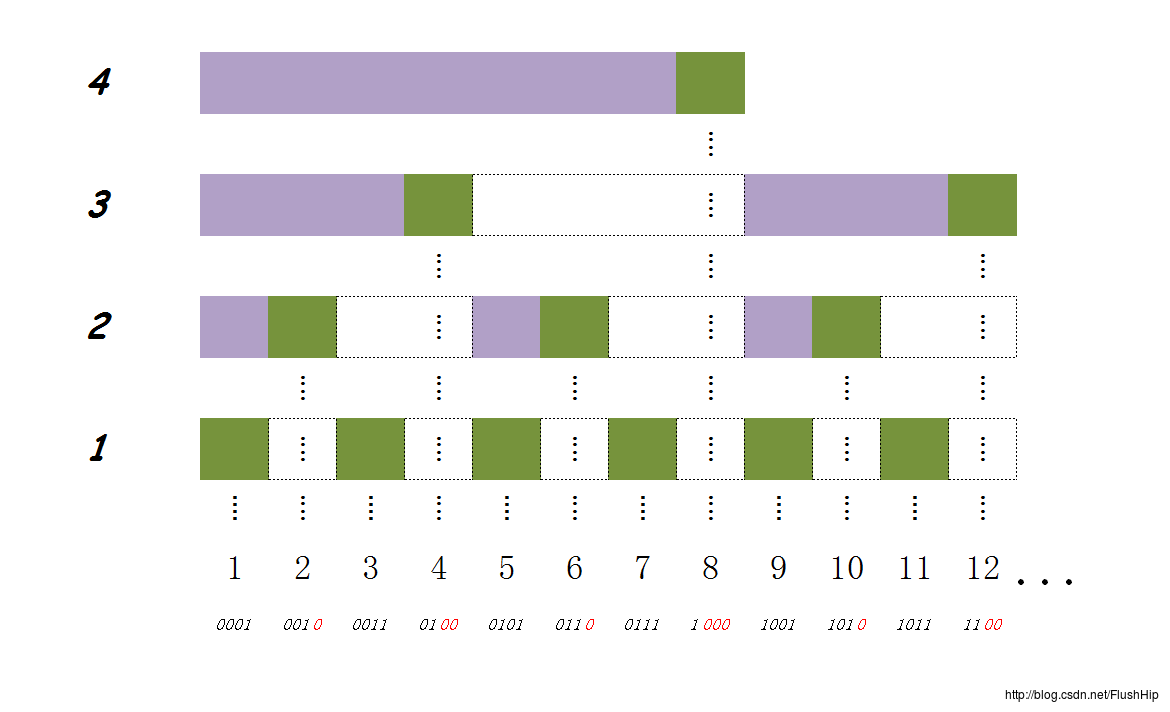首先放出大佬的博客:树状数组 树状数组 树状数组 树状数组中的二进制使用的很多,很多都是使用位运算来实现的。
说到树状数组,我们就可以知道线段树, 两者之间是有相同点的,但是也是有一些不同点的,列举如下:
具体区别和联系如下:
1.两者在复杂度上同级, 但是树状数组的常数明显优于线段树, 其编程复杂度也远小于线段树.
2.树状数组的作用被线段树完全涵盖, 凡是可以使用树状数组解决的问题, 使用线段树一定可以解决, 但是线段树能够解决的问题树状数组未必能够解决.
3.树状数组的突出特点是其编程的极端简洁性, 使用lowbit技术可以在很短的几步操作中完成树状数组的核心操作,其代码效率远高于线段树。
上面出现了一个新名词:lowbit.其实lowbit(x)就是求x最低位的1;
树状数组的结构
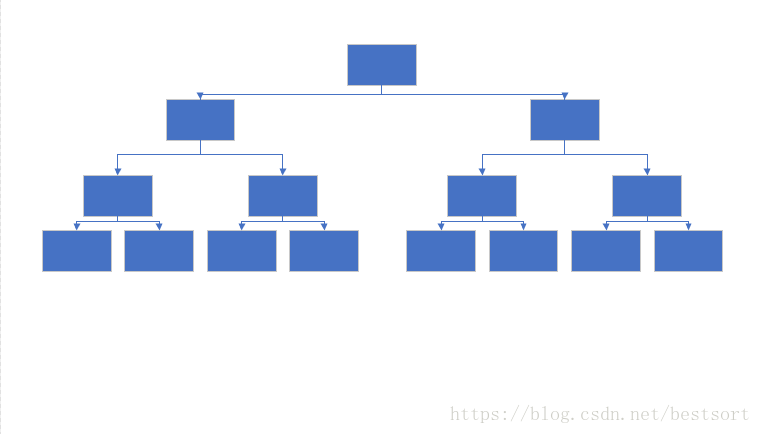
首先我们先了解树状数组的结构,这个是最重要的,树状数组的结构上使用二进制思想,我们再来使用十进制就很难理解了,我们应该将 十进制的角度转向二进制角度。
由这个图我们看出,有着明显的二叉树结构,但是树状数组也不是一个二叉树,只不过一些节点的位置有所改变,我们将点的位置改变,有的节点所表达的意义就不一样了。
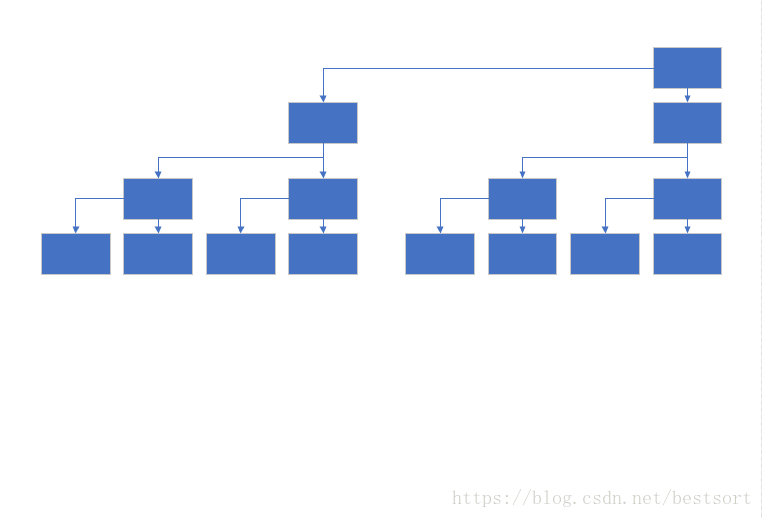
这个图像画的再详细一点就是下面这个图:
我们就可以看到,二进制与这个树状数组之间的关系,在线段树中,很明显的二叉树结构,是个完全二叉树,而树状数组不是一个二叉树结构,而是一个更加复杂的结构。
图中的绿色区域
图中的绿点就是原始的数据,我们将原始数据存于一个数组。
图中的紫色区域
图中紫色的区域就是树状数组“区间加和”的意思,比如c[4]=c[1]+c[2]+c[3]+c[4],不仅仅是包含着一个节点,还包含着一段区间,这段区间也是符合线段树中的“加法”性质的,比如:和,最大值,最小值等。
区间性质
上面的图也告诉我们,这个紫色区域在这个绿色区域的前面,我们就知道,某某节点的一个数据和是这一个区间中所有节点的数据和,这个是后缀和,就是这个点之前的和,区间的长度各个不同,有的相同,这个是很重要的,在后面的更新和查询中有很大的作用。
区间怎么分
树状数组区间分的方法与线段树不一样,线段树是二分,树状数组是位操作分的。(其中的一些操作我也不是很会,都是一些二进制的位操作)。我们看到上面图中,有很多层,我们看底下第一层所对的二进制是 0001,0011,0101,0111,1001,1011,我们从右到左第一个1是第一位,在树状数组中区间长度是1,我们再看第二层,0010,0110,1010,从右到左第一个1是第二位,我们再看这个区间节点的长度是2, 而我们看到第三层,二进制 0100,1100,从右到左第一个1是第三位,所以区间长度为 4,以此类推:
0001,0011,0101,0111,1001,1011 区间长度为1
0010,0110,1010 区间长度为2
0100,1100 区间长度为4
1000 区间长度为8
我们现在就是有一个问题,那么我们怎么来求这个最低位的1呢?这个问题(我也不是很明白)下面来看看:
lowbit(x)
我们使用lowbit函数就可以找到这个最低位的1,这个有点你不好理解,比如我们要求解6的最低位的1,二进制为 110,lowbit(x)就是2。但是我们怎么来做呢,就是将这个二进制
先放出代码:来求出一个正数num的二进制原码,和-num负数的补码,我们就可以从中找出来规律,就是这个lowbit 函数可以找出一个二进制最低位的1所代表的的数字。
#include<iostream>
using namespace std;
#include<bits/stdc++.h>
void dfs(unsigned int x)
{
if(x==0)
return ;
dfs(x/2);
cout<<x%2;
}
int lowbit(int x) //重中之重
{
return ((x)&(-x));
}
int main()
{
unsigned int num;
while(cin>>num)
{
cout<<"正数X: "<<' '; dfs(num); cout<<endl;
cout<<"负数X: "<<' '; dfs(-num); cout<<endl;
cout<<"lowbit(X): "; cout<<lowbit(num)<<endl;
}
return 0;
}分区间和
我们知道了,这个二进制最低位的1就是这个节点的区间长度,我们就知道了一个节点所包括的范围了,[x-lowbit(x)+1,x],就是这个范围:a数组是原始数据数组。
c[1]=a[1]
c[2]=a[1]+a[2]
c[3]=a[3]
c[4]=a[1]+a[2]+a[3]+a[4]
c[5]=a[5]
c[6]=a[5]+a[6]
c[7]=a[7]
c[8]=a[1]+a[2]+a[3]+a[4]+a[5]+a[6]+a[7]+a[8]
知道这个之后,我们下面进行单点修改:
单点修改
我们现在只取区间和的例子,我们知道有的节点是一段区间和,我们修改的时候,我们也得修改覆盖他们的节点区间,我们怎么来做呢,我们现在还得需要一个性质。现在我们有一个区间为
就是我们修改节点1的时候,我们得修改[1,8]的一个树状数组,现在我要修改1节点的数据,由图我们看到,我们需要修改1,2,4,8这4个节点的数据,那么我们怎么更新呢?由这个我们发现,1,2,4,8 我们看到 1+1=2,2+2=4,4+4=8。我们现在从二进制出手,就是1+lowbit(1)就是2,2+lowbit(2)=4,4+lowbit(4)=8,单单一个例子还不足以证明,我们再举一个例子,我们现在要修改节点3的值,根据图我们现在需要修改3,4,8节点的数据,3的二进制是011,我们找到这个lowbit(3)是1,我们lowbit(3)+3=4,找到4之后更新节点4,然后4+lowbit(4)=8,我们再更新8。
修改节点1,1+lowbit(1)=2,lowbit(2)+2=4,4+lowbit(4)=8,结束条件是小于总区间的长度,
修改节点3,3+lowbit(3)=4,lowbit(4)+4=8,
修改节点5,5+lowbit(5)=6,lowbit(6)+6=8,
.... 我们就可以总结出一个规律,使用一个函数来解决单点修改。
代码:
#include<iostream>
#include<bits/stdc++.h>
#define lowbit(x) ((x)&(-x))
using namespace std;
const int maxn=1005;
int c[maxn];
int n;
void update(int x,int val)
{
for(int i=x;i<=n;i+=lowbit(i))
c[i]+=val;
}
int main()
{
return 0;
}就是这样我们就可以了。
单点查询
根据上面的单点修改,单点查询与单点修改相差无几,我们现在看图,我们现在想要求出从节点1到指定节点的数据和,我们举一个例子,我们现在要求出从节点1到节点7之间的数据和,我们现在看图,从节点7到节点6,再到节点4,细细的看二进制数之间的关系:
节点 7,二进制为0111
节点6,二进制为0110
节点4,二进制为0100,
我们可以看到二进制数不断的减少最低位的1,在单点修改的时候,使用到了二进制lowbit的操作,在这里我们也会使用lowbit操作,我们可以看到我们每次都是减少最低位的1,我们这次是不断地减少lowbit(i),与单点修改恰恰相反,我们对要查询的点不断减少lowbit(i),直到 i>=1,结束,就是下面这张图

代码:
#include<iostream>
#include<bits/stdc++.h>
#define lowbit(x) ((x)&(-x))
using namespace std;
const int maxn=1005;
int c[maxn];
int n;
void update(int x,int val)
{
for(int i=x;i<=n;i+=lowbit(i))
c[i]+=val;
}
int chaxun(int x)
{
int ans=0;
for(int i=x;i>=1;i-=lowbit(i))
ans+=c[i];
return ans;
}
int main()
{
return 0;
}注意
树状数组有一些操作,比如区间修改+区间查询 和 区间修改+单点查询 和 单点修改+区间查询 的操作是不一样的,下面我们一个一个的来讲解。
单点修改+区间查询
单点修改上面说过了,这里主要说一下这个区间查询,我们上面已经说过单点查询,但是求出来的结果是从节点1到指定节点的和,我们可以这样想,有一个区间 [l,r],我们先求出chaxun(r),然后我们再求出chaxun(l-1),这样我们就可以使用 chaxun(r)-chaxun(l-1)就是这个区间的和。
代码:就是这样。
int chaxun(int x)
{
int ans=0;
for(int i=x;i>=1;i-=lowbit(i))
ans+=c[i];
return ans;
}
int chaxun_query(int x,int y)
{
return chaxun(y)-chaxun(x-1);
}区间修改+单点查询
先放出代码 :
void update(int x,int val)
{
for(int i=x;i<=n;i+=lowbit(i))
c[i]+=val;
}
void update_query(int x,int y,int val)
{
update(x,val);
update(y+1,-val);
}
int chaxun(int x)
{
int ans=0;
for(int i=x;i>=1;i-=lowbit(i))
ans+=c[i];
return ans;
}这里,区间修改是一个新的知识点叫做 差分,我们知道单点修改,修改一个节点,我们得将覆盖这个节点的节点都修改一遍,在区间修改中,我们使用单点修改会不免造成错误,因为修改了没有要求的节点,举个例子
我们要修改区间 [1,3]区间的值,我们在单点修改节点1的时候, 我们要修改 1,2,4,8 节点(假设总区间长度为8),我们这样修改的话,我们多修改了 4,8,节点,我们得消除多余节点的影响,我们该怎么做呢?
在这里我们又想到了二进制的那张图,我们可以这样想,消除后面节点的影响,一个区间[l,r],比如修改值 ,将区间内值增加 val,那么 我们可以在 r+1 往后的节点,增加 -val,来消除影响 ,在这里,你可能会有疑问
我们举一个例子:
[1,3]区间,我们多修改了 4, 8,节点,在修改 节点 4,8 增加-val ,将影响消除了 ,现在修改值为 1
先进行节点1的修改 ,成为下面。
![]()
现在我们修改 节点4(3+1),可以看到 4,8,节点的1消失了,这样我们可以消除影响
![]()
但是
如果我们不能精确的消除掉影响呢? (这句话是什么意思呢?)上面的消除影响的原理是使用二进制,节点1 进行修改的是 1,2,4,8,节点,我们正好消除4,8 节点的影响,这是恰好修改区间 挑选的好,如果我们挑选
[1,4]区间增加1,这时我们再来看看效果是什么样的,1,2,4,8 节点改变
![]()
我们再来修改 节点 5(4+1),增加值为 -1,效果![]()
我们看到 节点 5,6 的值 变为了-1,但是 节点 8的1消除了 ,这是为什么呢 ?我们再从上面的二进制图中找找答案,

对于5,6,8,节点的值变为 -1是肯定的,因为是一层一层覆盖的,8节点我们消除了影响,但是 5,6,节点又多了-1,那么我们怎么办呢?看下面这个图

其实这个是不用担忧的,当我们在查询的时候,我们单点查询 节点5,我们可以看到,结果是0,这个是为什么呢?明明显示的是-1呢?这时我们再看上面的树状数组的图片,并且联系上单点查询,我们看到, 设置ans=0,ans+=c[5]+c[4]=1+(-1)=0,就是这样,我们利用了一下二进制的原理,我们也使用了差分的原理,先对一部分区间实现加上 val,对于其他的部分区间我们加上-val ,这样我们就可以将差值保存下来(当然是按照二进制的原理来加的,以便在查询时方便),就这样,轻松的解决了区间修改的问题。
区间修改+区间修改
这个是这几个操作中最复杂的一个,也是最难的一个。
你可能有这样的疑惑,上面不是已经分别说了区间查询和区间修改了吗,为什么我们不能直接照搬上面的做法,为什么我们要重新设置一个方法。
下面我说一下,为什么我们上面的那些用法不能用了,我们已经知道,上面的区间修改和单点修改只是适用于一个节点的查询,而不是一段区间的查询,因为我们只是利用差分,只能求出来单个节点的数据,不能求出来一段区间的数据,那么我们怎么来求出一段区间的数据呢?
原理
既然我们知道了单个节点数据怎么求,我们只需要来几个一段区间节点的和,就像a[1]=d[1] ,a[2]=d[1]+d[2],a[3]=d[1]+d[2]+d[3]....... ,我们要求[2,3]区间的和的时候,我们就直接拿出a[3]-a[1],就可以了,我们得先构造出前缀和,才能使用。
构造前缀和
既然我们一个点的数据知道怎么来获得,那我们可以构造一个 前缀和数组 ,就是d[1] ,d[1]+d[2],d[1]+d[2]+d[3] ......,这样的一个数组,我们叫做节点p的前缀和:

在等式最右侧的式子∑pi=1∑ij=1d[j]∑i=1p∑j=1id[j]中,d[1]d[1] 被用了pp次,d[2]d[2]被用了p−1p−1次……那么我们可以写出:
位置p的前缀和 =

然后我们就知道了这个区间和是怎么弄出来的了,首先我们需要两个数组来维护树状数组,
sum1[i]=d[i];
sum2[i]=d[i]*i;
代码:
#include<iostream>
#include<bits/stdc++.h>
#define lowbit(x) ((x)&(-x))
using namespace std;
const int maxn=1005;
int c[maxn];
int n;
int sum1[maxn];
int sum2[maxn];
void update(int p,int val)
{
for(int i=p;i<=n;i+=lowbit(i))
{
sum1[i]+=val;
sum2[i]+=p*val;
}
}
void update_query(int x,int y,int val)
{
update(x,val);
update(y+1,-val);
}
int chaxun(int p)
{
int ans=0;
for(int i=p;i>=1;i-=lowbit(i))
ans+=(p+1)*sum1[i]-sum2[i];
return ans;
}
int chaxun_query(int x,int y)
{
return chaxun(y)-chaxun(x-1);
}
int main()
{
return 0;
}最大,最小值
单点查询
首先放出博客: 区间最值
我们现在放出 m个操作,其中有将每个节点的值换为其他值,还有操作是查询从1节点到指定节点的最大值,我们使用线段树就很好的解决问题,但是代码量很大,但是树状数组怎么来做呢?我们上面已经学会了求和的一堆东西,但是最大值,最小值,跟上面没有太大的关系,我们需要重新想方法。
我们不能只使用一个数组就可以完成修改值和更新最大值,所以我们需要一个维护数组来帮忙。我们每一次修改节点值,先更新维护数组,然后我们都要将树状数组清空,使用维护数组来再一次填充树状数组, 想法很简单,但是复杂度有 n*log(n),这个复杂度还是很大的,代码:
没有优化版
#include<iostream>
#include<bits/stdc++.h>
#define lowbit(x) ((x)&(-x))
using namespace std;
const int maxn=1005;
int h[maxn];
int a[maxn];
int n,m;
void update(int x,int val)
{
for(int i=x;i<=n;i+=lowbit(i))
h[i]=max(h[i],val);
}
int chery(int x)
{
int ans=-1;
for(int i=x;i>=1;i-=lowbit(i))
ans=max(ans,h[i]);
return ans;
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>a[i];
update(i,a[i]);
}
int index,val;
int flag;
while(m--)
{
cin>>flag;
if(flag==1)
{
cin>>index>>val;
memset(h,0,sizeof(h));
a[index]=val;
for(int i=1;i<=n;i++)
update(i,a[i]);
}
else
{
cin>>index;
cout<<chery(index)<<endl;
}
}
return 0;
}
我们现在想着是不是有着更好的算法,是不是有着优化方案,事实证明,是有的,那么我们怎么来实现呢?我们没有必要每次都要清空树状数组,那么我们怎么来实现呢?
有的区间是一段区间的覆盖,我们在修改这个区间的时候,我们得考虑到被覆盖区间的最大值和最小值,所以我们每次修改一个点,我们都要去他的子区间里面去寻找最大值,看图:
我们举一个例子,修改3节点,我们的主要方向是3-》4-》8,这个是大方向 ,但是每一个节点的子区间我们也要去逛,因为我们避免不了,大区间内有更大的数据的小区间,我们也要去遍历,找到更大的数据,我们要更新。下图中,我已经标了 标记,圈1,圈2,圈3,分别表示大方向,然后每次去遍历子区间。

优化版
#include<iostream>
#include<bits/stdc++.h>
#define lowbit(x) ((x)&(-x))
using namespace std;
const int maxn=1005;
int h[maxn];
int a[maxn];
int n,m;
void update(int x)
{
while(x<=n)
{
int len=lowbit(x);
h[x]=a[x];
for(int i=1;i<len;i<<=1)
h[x]=max(h[x],h[x-i]);
x+=lowbit(x);
}
}
int chery(int x)
{
int ans=-1;
for(int i=x;i>=1;i-=lowbit(i))
ans=max(ans,h[i]);
return ans;
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>a[i];
update(i);
}
int flag,index,val;
while(m--)
{
cin>>flag;
if(flag==1)
{
cin>>index>>val;
a[index]=val;
update(index);
}
else
{
cin>>index;
cout<<chery(index)<<endl;
}
}
return 0;
}
这样我们就可以以 O((logn)^2)的复杂度解决最大值,极大地降低了复杂度。
区间查询
上面是单点查询,下面我们求解区间查询最大小值,
直接照搬求区间合的方法显然是不行的。
因为区间合中,要查询[x,y]的区间合,是求出[1,x-1]的合与[1,y]的合,然后相减就得出了[x,y]区间的合。
而区间最值是没有这个性质的,所以只能够换一个思路。
设query(x,y),表示[x,y]区间的最大值
因为h[y]表示的是[y-lowbit(y)+1,y]的最大值。
所以,可以这样求解:
若y-lowbit(y) > x ,则query(x,y) = max( h[y] , query(x, y-lowbit(y)) );
若y-lowbit(y) <=x,则query(x,y) = max( a[y] , query(x, y-1);
这个递归求解是可以求出解的,且可以证明这样求解的时间复杂度是O((logn)^2)
我们就可以写出代码:
int chery(int x,int y) //
{
int ans = 0;
while (y >= x)
{
ans = max(a[y], ans);
y --;
for (; y-lowbit(y) >= x; y -= lowbit(y))
ans = max(h[y], ans);
}
return ans;
}我解读一下这段代码,可能会看不懂,我一开始也没有看懂是怎么来运行的。
首先,求解大方向是从右区间到左区间一步一步走的。有y>=x ,是个大前提,然后我们得分出两个步骤来解决
在这个代码中,我们可以看见 y--,我们很困惑,这个y--是个什么鬼?难道不是一路向左y-lowbit(y) 吗?答案是,不是一直向左减lowbit(y) ,我们可以看看例子,
y-lowbit(y) <=x
求解 [3,4] 区间最大值,我们这时 4-lowbit(4)=0 ,这时y就小于x了 ,我们如果没有拯救措施的话,我们求的就是[1,4]区间的最大值了,所以我们得避免这种情况出现,我们单独拎出来 4节点比较一下,然后 y--,变为3,我们再来比较。因为树状数组二进制的作用和区间段,我们得先看看是不是这段区间去减 lowbit(y) 后是不是已经比 x 小了 。
我们现在求解[2,3] 区间的最大值 ,虽然3-lowbit(3)=2,我们没有越界x,我们也可以进行y-- 的操作,这个也是没有错误的,所以我们为了避免上面的特殊情况,我们不管是不是上面的情况,我们都会进行y--。
y-lowbit(y)>x
这种情况,我们就只用考虑(x,y-lowbit(y))区间,和h[y] ,这个的结束条件是 是否满足 y-lowbit(y)>=x,避免出现越界的现象。
就是这样,解决问题。