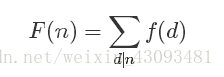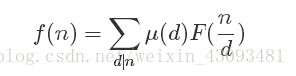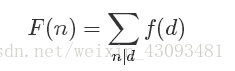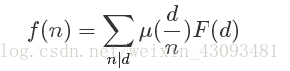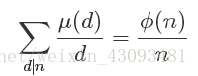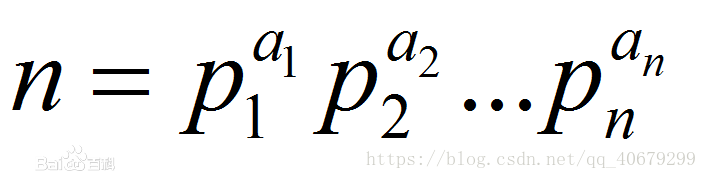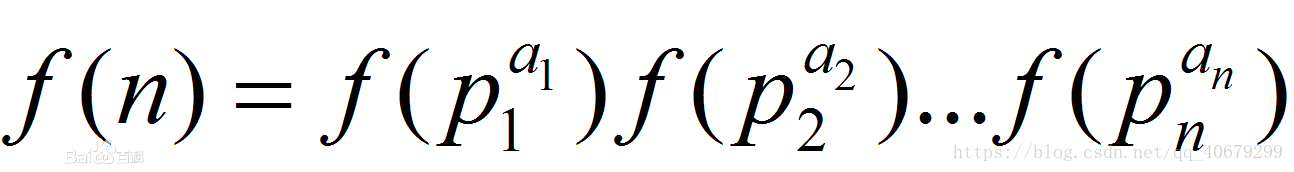数学：（一直很浮躁）

数论

算术基本定理

• 唯一质因数分解定理及其推论

威尔逊定理

威尔逊定理给出了判定一个自然数是否为素数的充分必要条件。即：当且仅当p为素数时：( p -1 )! ≡ -1 ( mod p )   //若p为质数，则p可整除(p-1)!+1。

欧拉定理：

对于互质的正整数a和n，有a^φ(n) ≡ 1(mod n)

费马小定理

费马小定理(Fermat's little theorem)是数论中的一个重要定理，在1636年提出。如果p是一个质数，而整数a不是p的倍数，则有a^（p-1）≡1（mod p）实际上，它是欧拉定理的一个特殊情况

卢卡斯定理：

   用于计算组合数取模，其中p必须是素数

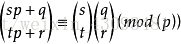
素数判定以及筛选

gcd 与 lcm

• 辗转相除法 与 更相减损术
• 最大公约数的性质
• 

• //gcd
  
  int gcd(int a,int b){
      if(b) return gcd(b,a%b);
      else return a;
  }
  
  //lcm
  int lcm(int a,int b)
  {
      return a/gcd(a,b)*b;
  }

贝祖定理与扩展欧几里得

• 贝祖定理：即如果a、b是整数，那么一定存在整数x、y使得ax+by=gcd(a,b)。换句话说，如果ax+by=m有解，那么m一定是gcd(a,b)的若干倍。（可以来判断一个这样的式子有没有解）有一个直接的应用就是 如果ax+by=1有解，那么gcd(a,b)=1；
• 扩展欧几里得 
• 已知整数a、b，扩展欧几里得算法可以在求得a、b的最大公约数的同时，能找到整数x、y（其中一个很可能是负数），使它们满足贝祖等式ax + by = gcd(a, b)。

乘法逆元

• 求法：
• 1.扩展欧几里得：ax≡1(mod n)可以等价的转化为ax−ny=1，利用exgcd解方程，并判断gcd(a,n)是否等于1
  若等于1，将x调整到1~n-1即可,O(logn)
  2.费马小定理：由a^(p−1)≡1(mod p)得a*a^(p−2)≡1(mod p)
  所以当模数是一个质数的时候，可以用费马小定理求解，即inv(i)=i^(p−2)(mod p) O(logn)
  3.欧拉定理： 由a^φ( p) ≡1(mod p)得a^ (φ( p)−1)是a的逆元
  适用于模数不是素数
• 摘抄了半天最后没保存，也是无语了
• 如果有ax≡1(mod n)，则称x是mod n意义下a的乘法逆元。记x=inv（a）或x=a^−1(定义了剩余系中的除法)
• 性质定理： 一个数有逆元<=>gcd(a,n)=1，此时逆元存在且唯一

• #include<iostream>
  #include<cstdio>
  #include<cstring>
  #include<algorithm>
  using namespace std;
  #define LL long long
  int inv[1000010];
  LL ksm(LL a,LL b,LL mod)      //费马小定理
  {
      int ans=1;
      while(b)
      {
          if(b&1) ans=(ans*a)%mod;
          a=(a*a)%mod;
          b>>=1;
      }
      return ans;
  }
  LL exgcd(LL a,LL b,LL &x,LL &y)   //扩展欧几里得
  {
      if(!b)
      {
          x=1;
          y=0;
          return a;
      }
      LL GCD=exgcd(b,a%b,x,y);
      LL tmp=x;
      x=y;
      y=tmp-a/b*y;
      return GCD;
  }
  LL inv1(LL a,LL mod)//扩展欧几里得求逆元
  {
      LL x,y;
      LL d=exgcd(a,mod,x,y);
      if(d==1) return (x%mod+mod)%mod;
      return -1;
  }
  LL inv2(LL a,LL mod)//费马小定理
  {
      return ksm(a,mod-2,mod);
  }
  void inv3(LL mod)//线性递推求1~n的所以逆元
  {
      inv[1]=1;
      for(int i=2;i<=mod-1;i++)
      {
          inv[i]=(mod-mod/i)*inv[mod%i]%mod;
          cout<<inv[i]<<" ";
      }
  }
  int main()
  {
      LL n,mod;
      while(cin>>n>>mod)
      {
          cout<<inv1(n,mod)<<" "<<inv2(n,mod)<<endl;
          inv3(mod);
      }
  }
  

   

欧拉函数

欧拉函数，用φ(n)表示欧拉函数是求小于等于n的数中与n互质的数的数目

（a与b互质）

（a与b不互质）

指数循环节

注意只有在B大于等于C的欧拉函数值时，才可以套用此公式；另外，如果b<φ(m)直接快速幂就可以了。

一元线性同余方程组：

1. 中国剩余定理（余数两两互质）

•               

void ex_gcd(LL a, LL b, LL &x, LL &y, LL &d){
    if (!b) {d = a, x = 1, y = 0;}
    else{
        ex_gcd(b, a % b, y, x, d);
        y -= x * (a / b);
    }
}
LL inv(LL t, LL p){//如果不存在，返回-1 
    LL d, x, y;
    ex_gcd(t, p, x, y, d);
    return d == 1 ? (x % p + p) % p : -1;
}
//n个方程：x=a[i](mod m[i]) (0<=i<n)
LL china(int n, LL *a, LL *m){//中国剩余定理 
    LL M = 1, ret = 0;
    for(int i = 0; i < n; i ++) M *= m[i];
    for(int i = 0; i < n; i ++){
        LL w = M / m[i];
        ret = (ret + w * inv(w, m[i]) * a[i]) % M;
    }
    return (ret + M) % M;
}

   2、比如，m1,m2, ... ,mn两两不保证互质，辣怎么办(っ °Д °)っ

• typedef long long LL;
  typedef pair<LL, LL> PLL;
  LL a[100000], b[100000], m[100000];
  LL gcd(LL a, LL b){
      return b ? gcd(b, a%b) : a;
  }
  void ex_gcd(LL a, LL b, LL &x, LL &y, LL &d){
      if (!b) {d = a, x = 1, y = 0;}
      else{
          ex_gcd(b, a % b, y, x, d);
          y -= x * (a / b);
      }
  }
  LL inv(LL t, LL p){//如果不存在，返回-1 
      LL d, x, y;
      ex_gcd(t, p, x, y, d);
      return d == 1 ? (x % p + p) % p : -1;
  }
  PLL linear(LL A[], LL B[], LL M[], int n) {//求解A[i]x = B[i] (mod M[i]),总共n个线性方程组 
      LL x = 0, m = 1;
      for(int i = 0; i < n; i ++) {
          LL a = A[i] * m, b = B[i] - A[i]*x, d = gcd(M[i], a);
          if(b % d != 0)  return PLL(0, -1);//答案，不存在，返回-1 
          LL t = b/d * inv(a/d, M[i]/d)%(M[i]/d);
          x = x + m*t;
          m *= M[i]/d;
      }
      x = (x % m + m ) % m;
      return PLL(x, m);//返回的x就是答案，m是最后的lcm值 
  }

高次同余方程（Baby Step Giant Step 算法）

ll power(ll a,ll b,ll p){
	ll ans = 1;
	while(b){
		if(b&1) ans = ans * a % p;
		b >>= 1;
		a = a * a % p;
	}
	return ans;
}
map<ll,ll> hap;
ll BSGS(ll a,ll b,ll p){
	hap.clear();
	b %= p;
	ll t = (ll)sqrt(p) + 1;
	for(ll j = 0;j < t;++j){
		ll val = (ll)b * power(a,j,p) % p;
		hap[val] = j;
	}
	a = power(a,t,p);
	if(a == 0) return b == 0?1:-1;
	for(ll i = 0;i <= t;++i){
		ll val = power(a,i,p);
		ll j = hap.find(val) == hap.end()?-1:hap[val];
		if(j >= 0 && i * t - j >= 0) return i * t - j;
	}
	return -1;
}

扩展BSGS

ll q_pow(ll a, ll b, ll mod){
    ll ans = 1;
    while(b){
        if(b & 1) ans = ans * a % mod;
        b >>= 1;
        a = a * a % mod;
    }
    return ans;
}

ll gcd(ll a,ll b){
    return b ? gcd(b,a%b) : a;
}

void ex_gcd(ll a,ll b,ll &x,ll &y){
    if(!b){
        x = 1;
        y = 0;
        return;
    }
    ex_gcd(b,a%b,y,x);
    y -= a / b * x;
    return;
}

ll exBSGS(ll a,ll b,ll p){
    a %= p;
    b %= p;
    ll ret = 1;
    for(ll i = 0; i <= 50; i++){
        if(ret == b) return i;
        ret = ret * a % p;
    }
    ll x,y,d,v = 1,cnt = 0;
    while((d = gcd(a,p)) != 1){
        if(b % d) return -1;
        b /= d;
        p /= d;
        v = v * (a / d) % p;
        cnt++;
    }
    map<ll,ll>h;
    ll m = ceil(sqrt(p)),t = 1;
    for(ll i = 0; i < m; i++){
        if(h.count(t)) h[t] = min(h[t],i);
        else h[t] = i;
        t = t * a % p;
    }
    for(ll i = 0; i < m; i++){
        ex_gcd(v,p,x,y);
        x = (x * b % p + p) % p;
        if(h.count(x)) return i * m + h[x] + cnt;
        v = v * t % p;
    }
    return -1;
}

莫比乌斯函数

定义:

若F(x)和f(x)满足：

则有：

或者
若F(x)和f(x)满足：

则有：

2.2性质：

1.若n>1且n为正整数，则有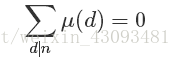，若n=1，则该式为1
2.对于任意正整数n均有：

组合数学

多重集排列与组合

多重集排列 ：

 有k个元素，其中第 i 个元素有  个，求 全排列的个数。

有n个不同的元素，每个元素可以选择多次，一共选 k 个元素，有多少种方法？

容斥原理

鸽巢原理

卢卡斯定理

Lucas定理是用来求 c(n,m) mod p，p为素数的值。

其他————————————————————————————————————————

积性函数

 积性函数指对于所有互质的整数a和b有性质f(ab)=f(a)f(b)的数论函数。

积性函数：若gcd(a,b)=1，且满足f(ab)=f(a)f(b)，则称f(x)为积性函数
完全积性函数：对于任意正整数a，b，都满足f(ab)=f(a)f(b)，则称f(x)为完全积性函数

1、若f(n),g(n)均为积性函数，则函数h(n)=f(n)g(n)也是积性函数
2.若f(n)为积性函数，则函数也是积性函数，反之一样
3.任何积性函数都能应用线性筛，在O(n)时间内求出1~n项

常见：

φ(n) －欧拉函数

μ(n) －莫比乌斯函数，关于非平方数的质因子数目

gcd(n,k) －最大公因子，当k固定的情况

d(n) －n的正因子数目

σ(n) －n的所有正因子之和——————>  例题

σk(n) － 因子函数，n的所有正因子的k次幂之和，当中k可为任何复数。

1(n) －不变的函数，定义为 1(n) = 1 （完全积性）

Id(n) －单位函数，定义为 Id(n) = n（完全积性）

Idk(n) －幂函数，对于任何复数、实数k，定义为Idk(n) = n^k （完全积性）

ε(n) －定义为：若n = 1，ε(n)=1；若 n > 1，ε(n)=0。别称为“对于狄利克雷卷积的乘法单位”（完全积性）

λ(n) －刘维尔函数，关于能整除n的质因子的数目

γ(n)，定义为γ(n)=(-1)^ω(n)，在此加性函数ω(n)是不同能整除n的质数的数目

另外，所有狄利克雷特征均是完全积性的

最小整数原理

最小数原理的另一种表述是：设N是全体自然数组成的集合，M是N的一个非空子集，则M中必有最小数

康扩展开

康托展开是一个全排列到一个自然数的双射，常用于构建哈希表时的空间压缩。 康托展开的实质是计算当前排列在所有由小到大全排列中的名次，因此是可逆的。

调和级数近似公式

  ((c为欧拉常数c=0.57721566490153286060651209))

但这个公式只能在n较大的时候使用，否则会有较明显误差，所以我们对小于1000000的n直接暴力求。

关于整数的分解

对于任意一个数正整数n，可以表示成10^a,其中a是个浮点数，例如：12=10^1.07918

矩阵快速幂

加速递推

数学归纳法

是一种利用递归思想证明的方法。如果要讨论的对象具有某种递归性质（如正整数），可以考虑用数学归纳法。

剩余类

剩余类，亦称同余类，是一种数学的用语，为数论的基本概念之一。设模为n，则根据余数可将所有的整数分为n类，把所有与整数a模n同余的整数构成的集合叫做模n的一个剩余类，记作[a]。并把a叫作剩余类[a]的一个代表元。

完全剩余系

从模n的每个剩余类中各取一个数，得到一个由n个数组成的集合，叫做模n的一个完全剩余系。完全剩余系常用于数论中存在性证明。

简化剩余系

简化剩余系(reduced residue system)也称既约剩余系或缩系，是m的完全剩余系中与m互素的数构成的子集，如果模m的一个剩余类里所有数都与m互素，就把它叫做与模m互素的剩余类。在与模m互素的全体剩余类中，从每一个类中各任取一个数作为代表组成的集合，叫做模m的一个简化剩余系。例如，模5的一个简化剩余系是1，2，3，4，模10的一个简化剩余系是1，3，7，9，模18的一个简化剩余系是1，5，7，11，13，17 [1]  。

狄里克雷素数定理

指出，对于任何两个正互素 整数 a和  d，存在无限多个形式为a  +  nd的素数，其中n也是一个正整数。换句话说，有无穷多个素数是一致的，以一模d。a  +  nd形式的数字构成算术级数

带余除法定理

对任意整数a，b>0，存在唯一的数对q，r，使a=bq+r，其中0≤r<b，这个事实称为带余除法定理，是整除理论的基础

除法取模

若有逆元，用扩欧法求。

无逆元公式

(a/b)%mod=a%(b*mod)/b%mod;

即

线性筛

二次剩余

当存在某个X，式子

 成立时，称“d是模p的二次剩余”

当对任意不成立时，称“ d是模 p的二次非剩余”