题目描述
Kiana 最近沉迷于一款神奇的游戏无法自拔。
简单来说,这款游戏是在一个平面上进行的。
有一架弹弓位于 (0,0)(0,0) 处,每次 Kiana 可以用它向第一象限发射一只红色的小鸟,小鸟们的飞行轨迹均为形如 y=ax^2+bxy=ax2+bx 的曲线,其中 a,ba,b 是Kiana 指定的参数,且必须满足 a < 0a<0,a,ba,b 都是实数。
当小鸟落回地面(即 xx 轴)时,它就会瞬间消失。
在游戏的某个关卡里,平面的第一象限中有 nn 只绿色的小猪,其中第 ii 只小猪所在的坐标为 \left(x_i,y_i \right)(xi,yi)。
如果某只小鸟的飞行轨迹经过了 \left( x_i, y_i \right)(xi,yi),那么第 ii 只小猪就会被消灭掉,同时小鸟将会沿着原先的轨迹继续飞行;
如果一只小鸟的飞行轨迹没有经过 \left( x_i, y_i \right)(xi,yi),那么这只小鸟飞行的全过程就不会对第 ii 只小猪产生任何影响。
例如,若两只小猪分别位于 (1,3)(1,3) 和 (3,3)(3,3),Kiana 可以选择发射一只飞行轨迹为 y=-x^2+4xy=−x2+4x 的小鸟,这样两只小猪就会被这只小鸟一起消灭。
而这个游戏的目的,就是通过发射小鸟消灭所有的小猪。
这款神奇游戏的每个关卡对 Kiana来说都很难,所以Kiana还输入了一些神秘的指令,使得自己能更轻松地完成这个游戏。这些指令将在【输入格式】中详述。
假设这款游戏一共有 TT 个关卡,现在 Kiana想知道,对于每一个关卡,至少需要发射多少只小鸟才能消灭所有的小猪。由于她不会算,所以希望由你告诉她。
输入输出格式
输入格式:
第一行包含一个正整数 TT,表示游戏的关卡总数。
下面依次输入这 TT 个关卡的信息。每个关卡第一行包含两个非负整数 n,mn,m,分别表示该关卡中的小猪数量和 Kiana 输入的神秘指令类型。接下来的 nn 行中,第 ii 行包含两个正实数 x_i,y_ixi,yi,表示第 ii 只小猪坐标为 (x_i,y_i)(xi,yi)。数据保证同一个关卡中不存在两只坐标完全相同的小猪。
如果 m=0m=0,表示Kiana输入了一个没有任何作用的指令。
如果 m=1m=1,则这个关卡将会满足:至多用 \lceil n/3 + 1 \rceil⌈n/3+1⌉ 只小鸟即可消灭所有小猪。
如果 m=2m=2,则这个关卡将会满足:一定存在一种最优解,其中有一只小鸟消灭了至少 \lfloor n/3 \rfloor⌊n/3⌋ 只小猪。
保证 1\leq n \leq 181≤n≤18,0\leq m \leq 20≤m≤2,0 < x_i,y_i < 100<xi,yi<10,输入中的实数均保留到小数点后两位。
上文中,符号 \lceil c \rceil⌈c⌉ 和 \lfloor c \rfloor⌊c⌋ 分别表示对 cc 向上取整和向下取整,例如:\lceil 2.1 \rceil = \lceil 2.9 \rceil = \lceil 3.0 \rceil = \lfloor 3.0 \rfloor = \lfloor 3.1 \rfloor = \lfloor 3.9 \rfloor = 3⌈2.1⌉=⌈2.9⌉=⌈3.0⌉=⌊3.0⌋=⌊3.1⌋=⌊3.9⌋=3。
输出格式:
对每个关卡依次输出一行答案。
输出的每一行包含一个正整数,表示相应的关卡中,消灭所有小猪最少需要的小鸟数量。
输入输出样例
输入样例#1: 复制
2
2 0
1.00 3.00
3.00 3.00
5 2
1.00 5.00
2.00 8.00
3.00 9.00
4.00 8.00
5.00 5.00输出样例#1: 复制
1
1输入样例#2: 复制
3
2 0
1.41 2.00
1.73 3.00
3 0
1.11 1.41
2.34 1.79
2.98 1.49
5 0
2.72 2.72
2.72 3.14
3.14 2.72
3.14 3.14
5.00 5.00输出样例#2: 复制
2
2
3
输入样例#3: 复制
1
10 0
7.16 6.28
2.02 0.38
8.33 7.78
7.68 2.09
7.46 7.86
5.77 7.44
8.24 6.72
4.42 5.11
5.42 7.79
8.15 4.99输出样例#3: 复制
6
说明
【样例解释1】
这组数据中一共有两个关卡。
第一个关卡与【问题描述】中的情形相同,22只小猪分别位于(1.00,3.00)(1.00,3.00)和 (3.00,3.00)(3.00,3.00),只需发射一只飞行轨迹为y = -x^2 + 4xy=−x2+4x的小鸟即可消灭它们。
第二个关卡中有55只小猪,但经过观察我们可以发现它们的坐标都在抛物线 y = -x^2 + 6xy=−x2+6x上,故Kiana只需要发射一只小鸟即可消灭所有小猪。
【数据范围】
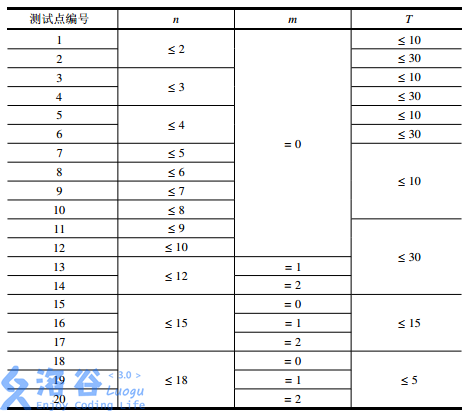
解法一:预处理所有能一次打掉的鸟的集合sta,转移方程,f[i]=min{f[i^sta],若sta为i的子集。复杂度为4^n,常数很小。
#include<bits/stdc++.h>
#define f(i,l,r) for(i=(l);i<=(r);i++)
using namespace std;
const int MAXN=20;
double EPS=1e-6;
int T,n;
double x[MAXN],y[MAXN];
int sta[1<<MAXN],num;
int f[1<<MAXN];
int main()
{
ios::sync_with_stdio(false);
int i,j,k,m;
cin>>T;
while(T--){
memset(f,1,sizeof(f));
num=0;
cin>>n>>m;
f(i,0,n-1){
cin>>x[i]>>y[i];
sta[++num]=1<<i;
}
int ALL=(1<<n)-1;
f(i,0,n-1){
f(j,0,n-1){
if(i==j||fabs(x[i]-x[j])<=EPS) continue;
double a=(x[j]*y[i]-x[i]*y[j])/(x[i]*x[j]*(x[i]-x[j]));
double b=(x[j]*x[j]*y[i]-x[i]*x[i]*y[j])/(x[i]*x[j]*(x[j]-x[i]));
if(a>=-EPS) continue;
sta[++num]=(1<<i)|(1<<j);
f(k,0,n-1){
if(k==i||k==j) continue;
if(fabs(a*x[k]*x[k]+b*x[k]-y[k])<=EPS){
sta[++num]=sta[num-1]|(1<<k);
}
}
}
}
sort(sta+1,sta+1+num);
int L=unique(sta+1,sta+1+num)-(sta+1);
f[0]=0;
f(i,1,ALL){
f(j,1,L){
if((i|sta[j])==i){
f[i]=min(f[i],f[i^sta[j]]+1);
}
}
}
cout<<f[ALL]<<endl;
}
return 0;
}解法二:预处理g[i][j]表示和i,j在同一条抛物线上的鸟。转移时分两种,一种是单独打一只鸟,一种是和其他鸟一起打。复杂度n^2*2^n。
#include<iostream>
#include<cstring>
#include<cmath>
#include<cstdio>
#define f(i,l,r) for(i=(l);i<=(r);i++)
#define EPS 1e-6
using namespace std;
double x[20],y[20];
int g[20][20],f[262150];
int T,n,m;
int main()
{
ios::sync_with_stdio(false);
int i,j,k;
cin>>T;
while(T--){
memset(g,0,sizeof(g));
cin>>n>>m;
f(i,0,n-1){
cin>>x[i]>>y[i];
}
f(i,0,n-1){
f(j,0,n-1){
if(i==j) continue;
double a=(x[j]*y[i]-x[i]*y[j])/(x[i]*x[j]*(x[i]-x[j]));
double b=(x[j]*x[j]*y[i]-x[i]*x[i]*y[j])/(x[i]*x[j]*(x[j]-x[i]));
if(a<=EPS)
f(k,0,n-1){
if(fabs(a*x[k]*x[k]+b*x[k]-y[k])<=EPS){
g[i][j]|=1<<k;
}
}
}
}
f[0]=0;
f(i,1,(1<<n)-1){
f(j,0,n-1){
if(i&(1<<j)) break;
}
f[i]=f[i^(1<<j)]+1;
f(k,0,n-1){
if(k==j||(i&(1<<k))==0) continue;
f[i]=min(f[i],f[i^(i&g[j][k])]+1);
}
}
cout<<f[(1<<n)-1]<<endl;
}
return 0;
}解法三:
若令 xx为满足 S\&(1<<(x-1))=0 的最小正整数,则由 SS 扩展的转移的所有线都要经过 x。
为什么?这个是对的吗?不经过 x就会慢吗?
你想一想,先打 1,4,再打 2,3,和先打 2,3,再打 1,4 是不是一样的?
如果这一次转移不打 x,那以后还要再回过头来打 x。这就是多余的转移。
因为经过 x 的线数量是 n,所以每次转移涉及到的线就从 n^2 变成了 n。
只要预处理一下 0-2^{18} 的对应的 x就能做到 O(Tn2^n)了,这才是考场的正解。
#include<bits/stdc++.h>
using namespace std;
const double eps=1e-8;
int t,n,m,lines[19][19],lowunbit[1<<19],dp[1<<19]; //lowunbit就是题解中的x
double x[19],y[19];
void equation(double &x,double &y,double a1,double b1,double c1,double a2,double b2,double c2){ //解方程
y=(a1*c2-a2*c1)/(a1*b2-a2*b1);
x=(c1-b1*y)/a1;
}
int main(){
for(int i=0;i<(1<<18);i++){ //预处理lowunbit
int j=1;
for(;j<=18 && i&(1<<(j-1));j++);
lowunbit[i]=j;
}
scanf("%d",&t);
while(t--){
memset(lines,0,sizeof(lines)); //各种初始化
memset(dp,0x3f,sizeof(dp));
dp[0]=0;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%lf%lf",x+i,y+i);
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++){ //处理所有抛物线
if(fabs(x[i]-x[j])<eps) continue; //x坐标相同,不可能有解
double a,b;
equation(a,b,x[i]*x[i],x[i],y[i],x[j]*x[j],x[j],y[j]);
if(a>-eps) continue; //解出a和b
for(int k=1;k<=n;k++)
if(fabs(a*x[k]*x[k]+b*x[k]-y[k])<eps) lines[i][j]|=(1<<(k-1));
}
for(int i=0;i<(1<<n);i++){ //重点!状压开始!
int j=lowunbit[i]; //必须经过lowunbit这个点
dp[i|(1<<(j-1))]=min(dp[i|(1<<(j-1))],dp[i]+1); //单独转移
for(int k=1;k<=n;k++) dp[i|lines[j][k]]=min(dp[i|lines[j][k]],dp[i]+1); //所有经过lowunbit的抛物线
}
printf("%d\n",dp[(1<<n)-1]); //答案
}
}记忆化搜索写法:
#include<bits/stdc++.h>
#define f(i,l,r) for(i=(l);i<=(r);i++)
using namespace std;
const int MAXN=19;
double EPS=1e-6;
int T,n,m;
double x[MAXN],y[MAXN];
int g[MAXN][MAXN];
int f[1<<18];
void dfs(int sta)
{
int i,j;
f(i,0,n-1){
if((sta&(1<<i))==0) break;
}
f(j,0,n-1){
if(f[sta|g[i][j]]>f[sta]+1){
f[sta|g[i][j]]=f[sta]+1;
dfs(sta|g[i][j]);
}
}
}
int main()
{
ios::sync_with_stdio(false);
int i,j,k;
cin>>T;
while(T--){
memset(f,1,sizeof(f));
memset(g,0,sizeof(g));
cin>>n>>m;
f(i,0,n-1){
cin>>x[i]>>y[i];
}
f(i,0,n-1){
f(j,0,n-1){
if(i==j){
g[i][j]=1<<i;
continue;
}
double a=(x[j]*y[i]-x[i]*y[j])/(x[i]*x[j]*(x[i]-x[j]));
double b=(x[j]*x[j]*y[i]-x[i]*x[i]*y[j])/(x[i]*x[j]*(x[j]-x[i]));
if(a<=-EPS)
f(k,0,n-1){
if(fabs(a*x[k]*x[k]+b*x[k]-y[k])<=EPS){
g[i][j]|=1<<k;
}
}
}
}
f[0]=0;
dfs(0);
cout<<f[(1<<n)-1]<<endl;
}
return 0;
}解法四:爆搜。
/*思路:搜索。
对于第i只猪,如果它已经被前面所构造的某条抛物线经过了,
就不用处理了,继续往下搜索。否则,就有两种选择,第一种
是与前面某一只单独的猪(即这只猪未与其它猪组成抛物线)
组成抛物线,因为两只猪最多也只能被一条抛物线相连;第二
种是暂时不与其它单独的猪组成抛物线。最后,将抛物线的条
数与余下的猪的个数相加(因为单独的一只猪也要一条抛物线
将其击中)就是搜索出来的一个合法的结果。*/
#include<iostream>
#include<cstdio>
#include<fstream>
#include<algorithm>
#include<string>
#include<sstream>
#include<cstring>
#include<cmath>
using namespace std;
const double eps=1e-8;
/*因为浮点数的精度计算太过复杂,像3.14这样的数存在浮
点型变量里存的可能是3.139999999,也有可能是3.140000001,
所以不能直接用“==”判断两个浮点数是否相等。在这种情况
下,就允许判断两个浮点数为相等时,两数之间存在微小的误差,
这个“微小的误差”要取一个较小的数,比如1e-8,这样就不
会判不出也不会误判了。*/
bool dy(double a,double b)//判断两个浮点数是否相等的函数
{
//如果a和b之间相差的值小于eps(即1e-8),就说明它们是相等的
return fabs(a-b)<eps;//fabs用于取浮点数的绝对值
}
int n=0,m=0,ans=0;
//x数组存每只猪的x坐标,y数组存每只猪的y坐标
//pwxa数组存每条已构造的抛物线的参数a,pwxb数组存每条已构造的抛物线的参数b
//tx数组存每只单独的猪的x坐标,ty数组存每只单独的猪的y坐标
double x[20],y[20],pwxa[20],pwxb[20],tx[20],ty[20];
//dfs(c,u,v)表示当前搜到第c只猪,已构造抛物线的数量为u,单独的猪的数量为v时的情况
//注意:当前抛物线的总数量为(u+v)条,因为除已有的抛物线外,每一只单独的猪也需要一条抛物线来击中它
void dfs(int c,int u,int v)
{
//最优性剪枝,因为即使后面的每一只猪都被当前已构造的抛物线击中,
//或者与其它单独的猪组成抛物线,抛物线的总数量还是(u+v),不会减少,
//所以如果抛物线的总数量已经大于等于当前的最优解时,搜下去也不会
//比当前更优了,就不用继续搜下去了。
if(u+v>=ans) return;
if(c>n)//如果搜完了
{
ans=u+v;//记录答案,因为前面已经有最优性剪枝了,所以没被剪掉的答案一定比当前更优
return;//结束
}
bool flag=false;//记录是否被已构造的抛物线经过
for(int i=1;i<=u;i++)//枚举已构造的抛物线
//将这一条抛物线的参数与当前猪的x坐标带进函数解析式算一遍,
//如果结果等于当前猪的y坐标,就说明当前猪已经被已构造的抛物线经过了
if(dy(pwxa[i]*x[c]*x[c]+pwxb[i]*x[c],y[c]))
{
dfs(c+1,u,v);//被经过了就直接往下搜
flag=true;//记录
break;//退出循环,既然当前猪已经被经过了,再继续判断也没有意义了
}
if(!flag)//如果没有被经过
{
for(int i=1;i<=v;i++)//枚举单独的猪
{
//如果当前猪与这一只单独的猪的x坐标相同,就说明它们不能组成一条
//抛物线。因为若想使它们组成一条抛物线,弹弓的位置就必须是它们的正下
//方,然后往上垂直发射,但是弹弓的位置固定在(0,0),而猪的x坐标又大于
//0(题目数据范围),所以它们不能组成一条抛物线。如果不加这个判
//断的话就会计算出一些奇奇怪怪的东西,影响后面的判断,所以还是加上为好。
if(dy(x[c],tx[i])) continue;//如果当前猪与这一只单独的猪的x坐标相同,跳过这一次循环
//求参数a、b的过程实际上就是解一个二元一次方程组,比如说有两只猪的坐标分别是(1,3)和(3,3),
//现在要求出它们所组成的抛物线的参数a与参数b。将两只猪的坐标分别代入到函数解析式中,
//就可以得出一个方程组: 3=a+b 3=9a+3b 。这是,我们可以用加减消元法消掉b,将两个方程
//分别乘上另一个方程的b的系数,得:9=3a+3b 3=9a+3b。这样,两个方程中的b的系数就一致了,
//然后直接用一个式子减去另一个式子,再将a的系数化为一即可。最后再将a带入到回任意一个方程求b即可。
//因为这里的所有方程都长一个样,所以这一种方法是通用的。
double a=(y[c]*tx[i]-ty[i]*x[c])/(x[c]*x[c]*tx[i]-tx[i]*tx[i]*x[c]);//求参数a
double b=(y[c]-x[c]*x[c]*a)/x[c];//将a代入求参数b
if(a<0)//如果这一个解是合法的,就说明当前猪与这一只单独的猪可以组成抛物线
{
pwxa[u+1]=a;//记录抛物线的参数a
pwxb[u+1]=b;//记录抛物线的参数b
//将这一只单独的猪从数组中删去,因为它已经和当前猪组成抛物线,不再单独了
double q=tx[i],w=ty[i];
for(int j=i;j<v;j++)
{
tx[j]=tx[j+1];
ty[j]=ty[j+1];
}
dfs(c+1,u+1,v-1);//继续往下搜
//将这一只单独的猪放回数组(回溯)
for(int j=v;j>i;j--)
{
tx[j]=tx[j-1];
ty[j]=ty[j-1];
}
tx[i]=q;
ty[i]=w;
}
}
//还有一种选择:暂时不与其它猪组成抛物线
tx[v+1]=x[c];
ty[v+1]=y[c];
dfs(c+1,u,v+1);//继续往下搜
}
}
int main()
{
int T=0;
scanf("%d",&T);
for(int Q=1;Q<=T;Q++)
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%lf%lf",&x[i],&y[i]);
ans=100;//记得初始化
dfs(1,0,0);//搜
printf("%d\n",ans);
}
return 0;//完美地结束
}