斐波那契数列的解有几种求法？

人做迭代，神做递归。
to iterate is human, to recurse, divine.
人们往往说只有神才能去理解递归，不仅仅是因为递归的深度一旦达到某种程度。人的大脑实在是无法想象，还因为递归是一种自顶向下的方式去思考问题的，有种从上帝角度看问题的意味。
今天我们通过斐波那契数列的n种求法来了解
代码究竟是通过什么方式写出
又是通过什么方式进行优化的？

第一种解法：递归求解

#include <cstdio>
#include <iostream>
//输入的n为正整数
int fibonacci(int n) {
	//若未到达递归基，递归求解前两项
	if (n > 2 ) {
		return fibonacci(n - 1) + fibonacci(n - 2);
	}
	//递归结束条件，到达基返回f(1)，f(2)的值
	if (n == 2 || n == 1) {
		return n - 1;
	}

}
//测试
int main() {
	int n;
	std::cin >> n;
	int result = fibonacci(n);
	std::cout << result;
}

以上这是我的个人写法
其实还可以通过三目运算符把程序再精简化：

#include <cstdio>
#include <iostream>
//输入的n为正整数
//骚操作：三目运算符
int fib(int n) {return (n < 3) ? n - 1 : fib(n - 1) + fib(n- 2);}
//测试
int main() {
	int n;
	std::cin >> n;
	int result = fib(n);
	std::cout << result;
}

我们求一下函数的时间复杂度：
T(1) = T(2) = 1,(n在1，2时只需一步O(1)得到答案）

T(n) = T(n-1) + T(n-2) + 1;（n > 2 时，需要递归，分别花上T(n-1）的时间和T(n-2)的时间，并将两步操作相加的时间O(1)
令：
S(n) = [T(n) + 1] / 2;
发现S(1) = fibonacci(2),
　　S(2) = fibonacci(3)
　　S(3) = fibonacci(4) = S(2) +S(1)
所以S(n) = fibonacci(n+1) = S(n-1) + S(n-2)
推出T(n) = 2 *S(n) - 1 = 2 *fibonacci(n+1) - 1
　　　　 = O(fibnacci(n+1))
由于斐波那契的通项公式由下图所示：

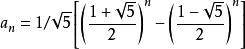
所以它的时间复杂度约等于O(2^n)
这个复杂度为指数级，当如果你要算第45项时，电脑就会开始卡顿，要将近等1秒，到第66项时，大概就要等1天。

第二种解法：记忆法递归优化

此方法仍然是对斐波那契递归，但是将每次递归所得到的值进行了存储，存到了f[n]数组里，需要用到时将其调用出来，也就是一共n组的数据，那么我们就将n组调用出来。

#include<iostream>
#include<cstring>
using namespace std;
int f[10000000];
int DFS(int n)
{
	if(f[n])
		return f[n];
	else
	{
		f[n]=DFS(n-1)+DFS(n-2);
		return f[n];
	}
}
int main()
{
	memset(f,0,sizeof(f));
	f[1]=1;
	f[2]=1;
	int n;
	cin>>n;
	DFS(n);
	cout<<DFS(n)<<endl;
	return 0;

此方法时间复杂度降低到了O（n），但是我们使用了数组将n组进行了存储，所以空间复杂度也达到了O（n）。

第三种解法： 动态规划继续优化

作为邓老师的小迷弟
他以前在课堂提到过一句名言
make it work,
make it right,
make it fast.
我们解问题：
首先我们让它运行成功，
然后我们让它没有bug，
最后我们让它运行快速。

第一种我们递归求解问题时是自上而下调用函数，这样会有可能出现重复调用的情况，速度较慢。
第二种我们递归时进行了记录，解决了重复调用的问题，但是空间开销因此却变大了。
而第三种，我们采用动态规划的思想去求解问题。

动态规划

(1)最优子结构：是指问题的最优解包含其子问题的最优解。

(2)子问题重叠：子问题重叠不是使用动态规划的必要条件，但是问题存在子问题重叠的特性更能够充分彰显动态规划的优势。

(3) 动态规划的维数：斐波那契数列问题中的递归方程中只涉及一个变量i，所以是一维的动态规划。

(4) 状态转移方程：

动态规划有两个解法：
1.通过自顶向下的备忘录解法（其实第二种解法也算一种动态规划的思想）
2.通过自下而上去求解问题，不会重复调用实例，这种方法一般通过迭代实现。
下图为我们遇到问题一般建立的数学建模方式：

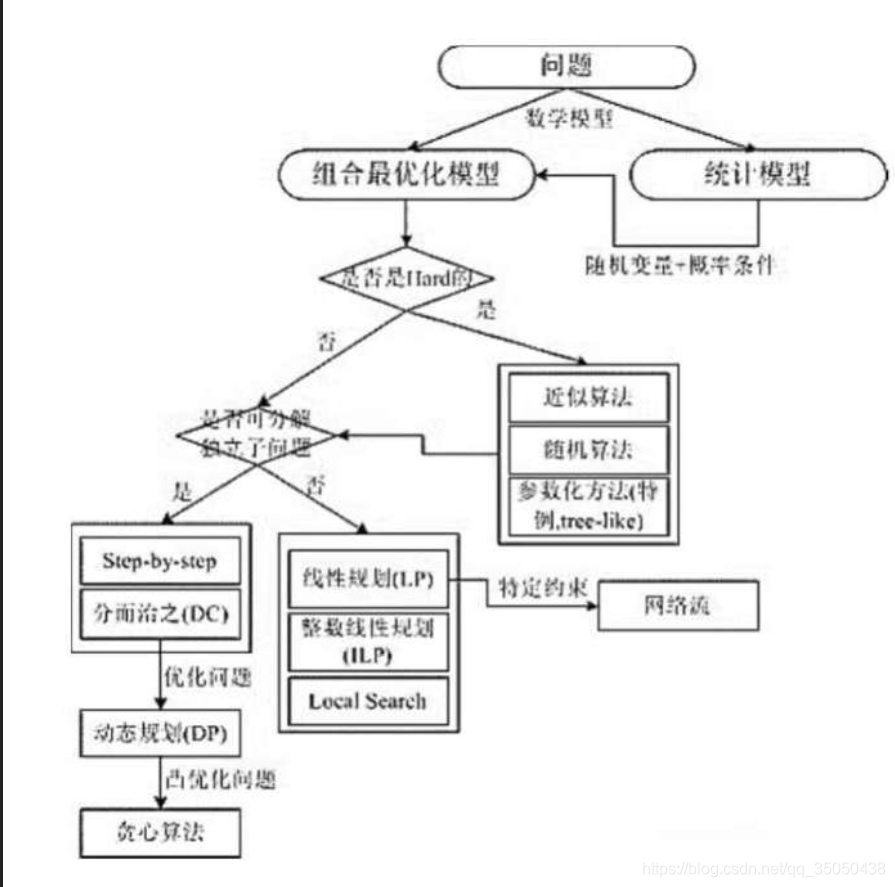
斐波那契数列的状态转移方程就是:
F(n) = F(n-1) + F(n-2)
我们发现当前求解状态只和前两项有关，所以只要每次计算时记录当前状态的前两项即可，代码如下：

#include <cstdio>
#include <iostream>
int fibonacci(int n)
{
	if (n <= 2)
		return n-1;
		
	int first = 0, second = 1, result;
	for (int i = 3; i <= n; i++)
	{
	//利用当前已知的两个值去求解下一个值，并更新当前两个值
		result = first + second;
		first = second;
		second = result;
	}
	
	return result;
}
//测试
int main() {
	int n;
	std::cin >> n;
	int result = fibonacci(n);
	std::cout << result;
}

此时我们只用了for循环用解决了问题，而且复杂度也下降到了O(n)线性级别的增长。
而且空间也只用到了O(1)级别，那简直太棒了！

第四种求解：矩阵快速幂求解

快速幂：一种快速乘方获取结果的做法

当我们计算2¹⁰⁰⁰的时候，我们计算机会将1000个2相乘得到结果，计算1000次。
因此我们用指数快速幂的方式，进行计算，指数快速幂是将指数变为二进制，通过二的次方来加快计算。
例：4³¹常规做法要计算31次4的乘积。计算乘次数31次
矩阵快速幂将31转换为二进制即：11111：2⁴ +2³ +2² +2¹+2⁰计算次数10次。
但显然：快速幂是对幂计算的较好的优化，但不一定是最好的优化。
显然我们这里计算2⁴拆成2³*2的形式，由于之前2³计算过，所以4次减少成了1次。
矩阵快速幂同理，不过我们要先从递推表达式中抽取出转移矩阵。

第一步：找到转移矩阵：

我们发现斐波那契数列可以提取的永恒的矩阵

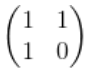
当我们不断往回推会发现最后变成

这个矩阵的n-1次方乘以一个f1和f2组成2行1列的矩阵

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod=1000000007;
typedef vector<ll> vec;//不定一维数组
typedef vector<vec> mat;//不定二维数组
//矩阵乘法，输入矩阵a和矩阵b
mat mul(mat &a,mat &b)
{
    mat c(a.size(),vec(b[0].size())); //矩阵相乘a*b 的矩阵与b*c的矩阵相乘得到a*c的矩阵
    for(int i=0; i<2; i++)//行更新
    {
        for(int j=0; j<2; j++)//列更新
        {
            for(int k=0; k<2; k++)
            {
                c[i][j]+=a[i][k]*b[k][j];//一行乘以一列
                c[i][j]%=mod;
            }
        }
    }
    return c;
}
mat pow(mat a,ll n)   //快速幂 
{
    mat res(a.size(),vec(a.size()));
    //把res作为单位矩阵乘以a矩阵的规模
    for(int i=0; i<a.size(); i++)
        res[i][i]=1;//单位矩阵；
    while(n)
    {
        if(n&1) res=mul(res,a);
        //让a矩阵乘以log2N次，
        a=mul(a,a);
        n/=2;
    }
    return res;
}
//a矩阵设为1101矩阵
ll solve(ll n)
{
    mat a(2,vec(2));
    a[0][0]=1;
    a[0][1]=1;
    a[1][0]=1;
    a[1][1]=0;
    a=pow(a,n);
    return a[0][1];//也可以是a[1][0];
}
//主函数测试
int main()
{
    ll n;
    while(cin>>n&&n!=-1)
    {
        cout<<solve(n)<<endl;
    }
    return 0;
}

我们可以看出矩阵快速幂的求解，矩阵乘法是常数级，while时间复杂度为O(log2N)
我们再次将时间复杂度降低到了log级别，而且几乎没有用到什么空间。

第六种解法： 公式求解

斐波那契的通项公式用数学方式已经求解出来，我们可以直接用代码将公式打上：

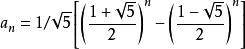
#include <csdio>
#include <iostream>
int main(){
	int n;
 	std::cin>>n;
 	result = 1/5^0.5 * ((1 + 5^0.5)/2)^n - ((1 - 5^0.5)/2)^n);
	std::cout<<result;
}

此方法最bug，**O(1)**解决，数学果然是最牛逼的学科。