1、排列与排列组合的联系与区别

谈到排列和排列组合的联系与区别时，我们先聊聊它们的定义与概念吧:

排列，一般地，从n个不同元素中取出m（m≤n）个元素，按照一定的顺序排成一列，叫做从n个元素中取出m个元素的一个排列(permutation)。特别地，当m=n时，这个排列被称作全排列(all permutation)。

排列组合是组合学最基本的概念。所谓排列，就是指从给定个数的元素中取出指定个数的元素进行排序。组合则是指从给定个数的元素中仅仅取出指定个数的元素，不考虑排序。

因而，总的来说，它们两的相同点就在于都是从n个不同的元素中取出m个元素(其中m<=n)，但不同的地方在于排列考虑取出的这m个元素的顺序,而排列组合并不考虑。

相同点还是比较好理解的，但是对于不同点的话，我们有必要对自己进行一个灵魂的拷问——这里所谓的顺序，指的是什么？

试着考虑以下两个场景:

场景1:
体育老师:“大家按高矮顺序排好队。”
童鞋们:“老师,从前往后排吗？矮的站前面高的站后面吗？”
体育老师:“废什么话！快点站就是了！”
童鞋们吓得一阵哆嗦，屁颠屁颠地排好了队。

场景2:
教官:“大家按高矮顺序排好队。”
童鞋们:“教官,咱是从左往右排吗？矮的站左边高的站在右边吗？”
教官:“废话！快点站好了！”
童鞋们吓得一阵哆嗦，屁颠屁颠地排好了队。

由此可见，在两个场景中，虽然体育老师和教官说的都是按“高矮顺序排好队“，但是由于所处的语境不同，语义也会有所差异。在没有明确的规定下，我们唯有根据自己的经验去揣测，而并不明晓其中的具体含义。在体育老师的认知里，他所认为的“按高矮顺序”，指的是“从前往后，前矮后高”，而在教官的认知里，他所认为的“按高矮顺序”，指的是“从左往右，左矮右高”。

所以，对于顺序，根据每个人理解的不同，它的含义也可能会有所不同。比如有的人认为按顺序来，指的是从小到大，有的人则认为是从大到小；有的人认为是从左往右，有的人却认为是从右往左；有的人认为是从高到低，但有的人认为是从低到高…

因此，说到底，对于顺序，我个人对它的理解就只是我们人类指定的一套规则或规范罢了，它并没有具体的含义。

所以，对于1,2,3的全排列的六种排列情况
[1,2,3]
[1,3,2]
[2,1,3]
[2,3,1]
[3,1,2]
[3,2,1]

你不能说[1,2,3]是按顺序排列的，而[3,2,1]就不是按顺序排列的，只不过[1,2,3]是按照从小到大的次序排列，而[3,2,1]是按照从大到小的次序排列。事实上，除此之外，并非只有[1,2,3]和[3,2,1]两种排列方式是按顺序排列的，剩下的[1,3,2],[2,1,3],[2,3,1],[3,1,2]也都是按顺序排列的，只不过是按照不同方式的顺序而已。

因而，对于中学里我们熟悉的排列与排列组合的公式
A(m,n) = n×(n-1)×(n-2)×…×(n-m+1)
与
C(m,n) = n×(n-1)×(n-2)×…×(n-m+1) / m!
，若m=3,n=3时,你不能说C(3,3) = 1的一种情况,是A(3,3)=6种情况中的具体其中的一种情况,因为对于C(3,3)来说，它只考虑从3个数中取3个数这个过程最终具体可能会有的情况种数，它只在乎结果，而不在乎过程。而对于A(3,3)来说，它不仅要考虑从3个数中取3个数这个过程的结果，也要考虑从这3个数中取出这3个数的过程。

然而虽说C(m,n)只考虑从n个数中取m个数这个过程最终具体可能会有的情况种数,但为了具象化地表示出这个结果，我们有必要人为地拟定一种方案,将它描述出来。

就我个人常采用的方案来看，我会将取出的m个数按依次递增的次序的顺序作为这个结果的具象化表示。

有了这个规定的话，对于排列组合我们就更好理解了，例如1,2,3的全排列A(3,3)=[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1],共6种，对应的排列组合就可以是C(3,3)=[1,2,3],共1种;1,2,3的排列A(2,3)=[1,2],[1,3],[2,1],[2,3],[3,1],[3,2],共6种,对应的排列组合就可以是C(2,3)=[1,2],[1,3],[2,3]，共3种。

2、对于排列与排列组合公式的理解

搞清楚了排列和排列组合的概念和含义之后，我们还有必要理解一下它们的公式
A(m,n) = n×(n-1)×(n-2)×…×(n-m+1)
与
C(m,n) = n×(n-1)×(n-2)×…×(n-m+1) / m!

首先是A(m,n)，即从n个物体中选m个的排列数，可以理解成n个人，选出m个最好的座位，按座次排列。第一个人有n种可能，第二个人有(n-1)种选择，…，第m名有 (n-m+1)种选择，所以总的选择（可能）数目是：
n*(n-1) * … *(n-m+1)= n!/(n-m)!

(其中n*(n-1)…(n-m+1)= n!/(n-m)!的推导过程为:
n*(n-1)…(n-m+1)
= n*(n-1)…(n-m+1) * (n-m) * (n-m-1)* … * 2 * 1 / (n-m) * (n-m-1) * … * 2 * 1 = n! / (n-m)!)

其次是C(m,n),在A(m,n)的基础上，可以理解成n个人,选出m个最好的座位，而这m个坐上座位的人，规定了一定的次序,可以规定为第一个人要坐在这第m个座位的第一排,第二个坐在这第m个座位的第二排，…,第m个人坐在这个座位的第m排，因而规定了次序之后,总的选择数目需除以这m个座位的排列次序,即m!:

所以
C(m,n) = n×(n-1)×(n-2)×…×(n-m+1) / m!
=n! / ((n-m)! * m!)

3、正整数区间[x,n]内的正整数个数

上面的公式推导看似让人恍然大悟，但我们可能忽略了一个问题,即对于A(m,n) = n×(n-1)×(n-2)×…×(n-m+1)的尾项(n-m+1)，以及第m名有 (n-m+1)种选择,我们如何理解其中(n - m + 1)的由来?

这时候便很有必要检验一下咱对上小学时常用的找规律与解方程的知识掌握了。

我们知道，对于正整数区间[2,5]或者我们日常生活中谈及的2到5,共有2 、3 、4 、5共4个正整数。不管你是数的，还是算的,甚至是猜的，都无关紧要，因为对于这个问题，它已经是我们的生活常识了,如果连这个问题都回答不出来，是很难在如今21世纪里生存下去的。

而对于正整数区间[2,50]或2-50，有2 、3 、4 、5…48、49、50，共49个正整数，如果这次你还是数的，虽说也可以数的出来，但这或许未免也太费劲了。以至于当区间扩大范围时，如[2,50000000],[2,5000000000000],“数"的方法，显然如此苍白无力。

那既然我们数不出来,这个问题却必须去面对与解决，想必便一定有数学公式我们可以用来求解它。

我们可以先试着考虑列举一些可能的情况：
对于[1,2],有1,2共2个正整数,
对于[1,3],有1,2,3共3个正整数,
对于[1,4],有1,2,3,4共4个正整数,
进而总结出规律:
对于[1,n],有1,2,…,n共n-1+1＝n个正整数,

同理,
对于[2,n],有2,3…n共n-2+1=n-1个正整数,
对于[3,n],有3,4…n共n-3+1=n-2个正整数,
进而总结出终极规律
定理1:对于正整数x,n分别作为下界与上界的区间[x,n],有x,x+1…n共n-x+1个正整数, 其中 x∈[1,n]

并由此类似的证明过程可推出衍生规律:
定理2:对于整数x,n分别作为下界与上界的区间[x,n],有x,x+1…n共n-x+1个整数, 其中 x∈[-n,n]

有了定理1和定理2的理论基础后，再来探究式子(n-m+1)的由来，就显得豁达开朗了。

对于排列的计算公式,有A(m,n) = n×(n-1)×(n-2)×…×(n-m+1)，而因为排列是从n个数中选出m个数,因而这m个数中第1个数有(n-0)种可能,第2个数有(n-1)种可能,第3个数有(n-2)种可能,…对于第k个数,设其有(n-x)种可能,这里显然x的最小值为0，而最大值运用定理2可知:若设最大值为p,则[0,p]内共有p-0+1=p+1个整数，欲使p+1=m，则p=m-1,因此对于第m个数，共有(n-(m-1))=(n-m+1)种可能。

(如果你对上面的证明过程看得似懂非懂的，也可以试试采用变量代换的方法：
对于排列的计算公式,有A(m,n) = n×(n-1)×(n-2)×…×(n-m+1)，而因为排列是从n个数中选出m个数,因而这m个数中第1个数有(n-0)种可能,第2个数有(n-1)种可能,第3个数有(n-2)种可能,…对于第k个数,设有(n-x)种可能,由之前的结论，可知x=k-1,所以对于第k个数,有(n-(k-1))=(n-k+1)种可能,进而对于第m个数，有(n-m+1)种可能。)

在基于理解了上述定理的前提下，对于排列组合的C(k,n),即从n个数中选出k个数,选出的这k个数的变化范围是什么,我们可以假设这n个数依次为1,2,…,n,从其中选k个数这k个数的最大值为n,设最小值为x,即这k个数的变化区间为[x,n],则运用定理2可得 n - x + 1 = k，进而得出x = n - k + 1,
同理设最小值为1，设最大值为x，则这k个数的变化区间为[1,x]，运用定理2可得x - 1 + 1 = k，进而得出x = k

4、用回溯法实现排列组合

要用回溯法实现排列组合，主要是需要理解如何由用回溯法实现全排列过渡至如何用回溯法实现组合排列。

我们先来看看对于全排列A(3,3)和组合排列C(3,3)的树状图
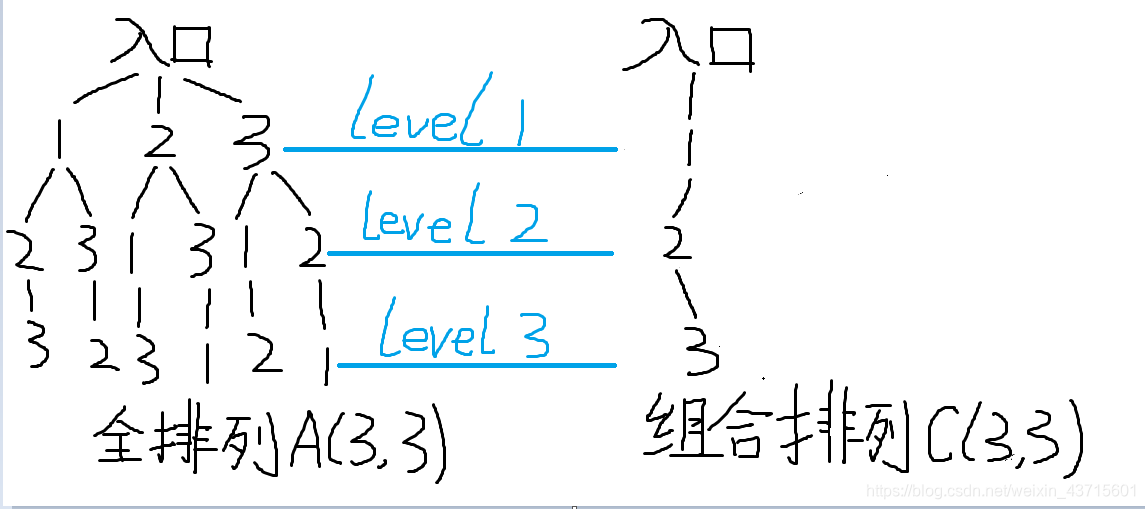
在这里插入图片描述

接着再来看看对于排列A(2,3)和组合排列C(2,3)的树状图
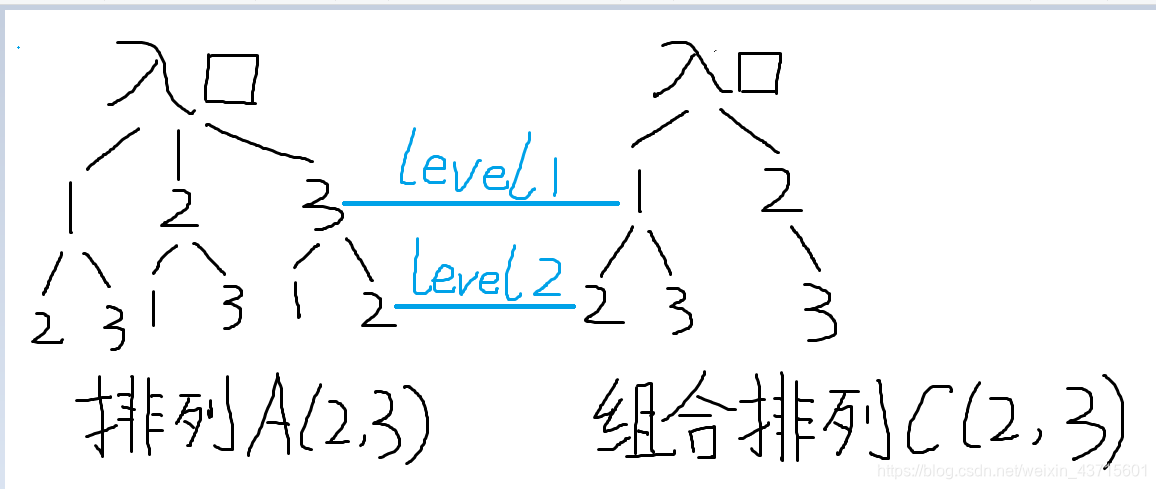
在这里插入图片描述
分析对比一番,我们可以发现:
对于排列A(k,n),n为树状图中树的主分支个数，而k为树状图中树的高度。且对于每一条分支路而言,当前高度h出现的数与前高度1,2,…h内出现的数都不同。

对于组合排列C(k,n),n-k+1为树状图中树的主分支个数，而k为树状图中树的高度。且对于每一条分支路而言,当前高度h出现的数不仅与前高度1,2,…h内出现的数都不同,且要比它们都要大。

基于此思想，我们则可以设计出如下算法:

#include<iostream>
using namespace std;
int visit[10];//用于标记数组a 
int a[10]; //用于存储输入数据
int b[10];//用于存储排列数据 
void dfs(int p,int k,int n){
	if(k == 0){
		for(int i = 1;i < p;i++){
		cout << a[b[i]]<< " ";	
		}
		cout << endl;
		return;
	}
	for(int i = 0;i < n - k + 1; i++){	    
		if(visit[i] == 0){
			visit[i] = 1;
			if(i > b[p - 1]){
			b[p] = i;
			dfs(p + 1,k - 1,n); 
		    }
			visit[i] = 0; 
		}	
	}
}
int main(){
	int n;
	int k;
	cin >> n >> k;  
	for(int i = 0;i < n; i++){
		cin >> a[i];
	}
	b[0] = -1;
	dfs(1,k,n);
}