题目传送门
分析:
如果直接猜这是个积性函数的话就要简单一些(相对的)了2333
但是我们要严谨(
大力推式子:
\(~~~~\sum_{i=1}^{n}\sum_{j=1}^{i}\sum_{k=1}^{i}lcm(gcd(i,j),gcd(i,k))\)
熟练的OI选手应该很快能推出这一步(错乱),如果这一步不能很快推出,建议先去做简单一点的题夯实一下基础(=w=):
\(~~~~\sum_{i=1}^{n}\sum_{d_1|i}\sum_{d_2|i}lcm(d_1,d_2)\varphi(\frac{i}{d_1})\varphi(\frac{i}{d_2})\)
令其等于\(\sum_{i=1}^{n}f(i)\)
然后后面就是极其神仙的推导
可是这个歪歪扣不仅丧病而且脑子不太好使,这里搬一下大佬skywalkert的推导
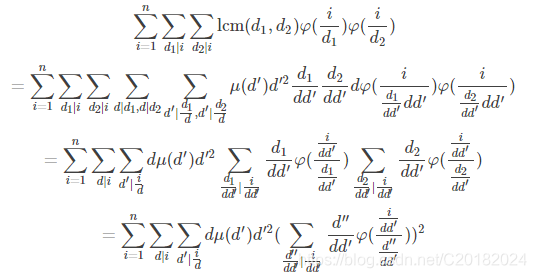
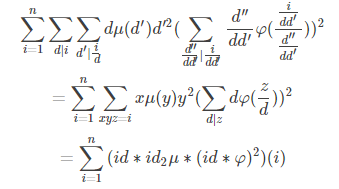
OrzOrz
最后那个是个卷起来的东东是积性函数,所以\(f(i)\)也是一个积性函数
OrzOrz
那么:
\(f(i)=\prod f(p_i^{a_i})\)
回到原式子开始试着推\(f(p^k)\):
\(~~~~f(p^k)=\sum_{i=1}^{p^k}\sum_{j=1}^{p^k}lcm(gcd(p^k,i),gcd(p^k,j))\)
\(=\sum_{i=0}^{k}\sum_{j=0}^{k}p^{max(i,j)}\varphi(p^{k-i})\varphi(p^{k-j})\)
\(=\sum_{i=0}^{k}p^i\varphi(p^{k-i})(2\sum_{j=0}^{i-1}\varphi(p^{k-j})+\varphi(p^{k-i}))\)
这里的小trick可以想一想
然后我们直接可以算出\(\varphi(p^k)\),一个一个带进去化简
过程繁琐,这里就不写了2333,用到的就是等比数列求和的简单知识
最后我们把式子推出来:
\(~~~~f(p^k)=(2k+1)(p^{2k}-p^{2k-1})+p^{k-1}\)
\(~~~~f(p)=3p^2-3p+1\)
我们结合一下min_25筛的要求:
1、\(f(p)\)是多项式函数
2、\(f(p^k)\)可以快速算出,这里可以用快速幂
那么接下来就是快乐的min_25筛了
\(\sum_{i=1}^{n}[i\in Prime]f(i)=3G_2(n,|P|)-3G_1(n,|P|)+G_0(n,|P|)\)
不知道在讲sm的可以看看这篇
然后直接筛就好了
unsigned int这个东西真恶心,好多细节搞我好久
有些小trick直接看代码吧
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<vector>
#include<iostream>
#include<map>
#include<string>
#define maxn 1000005
#define INF 0x3f3f3f3f
#define inv3 2863311531u
using namespace std;
inline unsigned int getint()
{
unsigned int num=0,flag=1;char c;
while((c=getchar())<'0'||c>'9')if(c=='-')flag=-1;
while(c>='0'&&c<='9')num=num*10+c-48,c=getchar();
return num*flag;
}
unsigned int N,S;
unsigned int pri[maxn],np[maxn],cnt,sumpri[maxn],sumpw[maxn];
unsigned int G0[maxn],G1[maxn],G2[maxn];
unsigned int num[maxn],tot;
unsigned int pos1[maxn],pos2[maxn];
inline void init()
{
for(unsigned int i=2;i<maxn;i++)
{
if(!np[i])pri[++cnt]=i,sumpri[cnt]=sumpri[cnt-1]+i,sumpw[cnt]=sumpw[cnt-1]+i*i;
for(unsigned int j=1;j<=cnt&&1ll*i*pri[j]<maxn;j++)
{
np[i*pri[j]]=1;
if(i%pri[j]==0)break;
}
}
}
inline unsigned int ksm(unsigned int num,unsigned int k)
{
unsigned int ret=1;
for(;k;k>>=1,num=num*num)if(k&1)ret=ret*num;
return ret;
}
inline unsigned int getf(unsigned int p,unsigned int k)
{return (2*k+1)*(ksm(p,2*k)-ksm(p,2*k-1))+ksm(p,k-1);}
inline unsigned int getsum(unsigned int n,unsigned int m)
{
if(n<2||pri[m]>n)return 0;
unsigned int k=(n<=S)?pos1[n]:pos2[N/n],ret=(3*G2[k]-3*G1[k]+G0[k])-(3*sumpw[m-1]-3*sumpri[m-1]+m-1);
for(unsigned int i=m;i<=cnt&&1ll*pri[i]*pri[i]<=n;i++)
{
unsigned int tmp=pri[i];
for(unsigned int j=1;1ll*tmp*pri[i]<=n;j++,tmp*=pri[i])
ret+=(getsum(n/tmp,i+1)*getf(pri[i],j))+getf(pri[i],j+1);
}
return ret;
}
int main()
{
init();
int T=getint();
while(T--)
{
tot=0;
memset(pos1,0,sizeof pos1),memset(pos2,0,sizeof pos2);
memset(G0,0,sizeof G0);memset(G1,0,sizeof G1);memset(G2,0,sizeof G2);
memset(num,0,sizeof num);
N=getint();
S=(unsigned int)(sqrt(N));
for(unsigned int i=1,j;i<=N;i=j+1)
{
j=N/(N/i);num[++tot]=N/i;
G0[tot]=num[tot]-1;
G1[tot]=(unsigned int)(1ull*num[tot]*(num[tot]+1)/2);G1[tot]--;
G2[tot]=(unsigned int)(1ull*num[tot]*(num[tot]+1)*(2*num[tot]+1)/2*inv3);G2[tot]--;
if(num[tot]<=S)pos1[num[tot]]=tot;
else pos2[j]=tot;
}
for(unsigned int j=1;j<=cnt;j++)
for(unsigned int i=1;i<=tot&&1ll*pri[j]*pri[j]<=num[i];i++)
{
unsigned int k=(num[i]/pri[j]<=S)?pos1[num[i]/pri[j]]:pos2[N/(num[i]/pri[j])];
G0[i]-=G0[k]-(j-1);
G1[i]-=pri[j]*(G1[k]-sumpri[j-1]);
G2[i]-=pri[j]*pri[j]*(G2[k]-sumpw[j-1]);
}
printf("%u\n",getsum(N,1)+1);
}
}