一、临界区
1.定义:临界区指的是一个访问共用资源(例如:共用设备或是共用存储器)的程序片段,而这些共用资源又无法同时被多个线程访问的特性。当有线程进入临界区段时,其他线程或是进程必须等待,有一些同步的机制必须在临界区段的进入点与离开点实现,以确保这些共用资源是被互斥获得使用。
2.临界区中存在的属性:
- 互斥:同一时间临界区中最多存在一个线程;
- Progress:如果一个线程想要进入临界区,那么它最终会成功(如果无限等待,处于饥饿状态,不妥);
- 有限等待:如果一个线程i处于入口区,那么在i的请求被接受之前,其他线程进入临界区的时间是有限制的;
- 无忙等待(可选):如果一个进程在等待进入临界区,那么它可以进入之前会被挂起。
二、管理临界区的方法
1. 禁用硬件中断
采用引荐中断需要考虑时钟中断:时钟中断是控制进程调度的手段之一
- 没有中断,没有上下文切换,因此没有并发。硬件将中断处理延迟到中断被启用之后;大多数现代计算机体系结构都提供指令来完成。
- 进入临界区,则禁用中断。
- 离开临界区,则开启中断。
但是,存在如下问题:
- 一旦中断被禁用,线程就无法被停止;整个系统都会为你停下;可能导致其他线程处于饥饿状态。
- 如临界区可以任意长,则无法限制响应中断所需的时间
2. 基于软件的解决方法
例子:假设有两个线程,T0和T1。Ti的通常结构为:
1 do{ 2 enter section //进入区域 3 critical section //临界区 4 exit section //离开区域 5 reminder section //提醒区域 6 }while(1);
线程可能共享一些共有的变量来同步他们的行为。下面设计一种方法,能在有限时间内实现退出/进入页区。
算法前置知识与考虑
- 共享变量,先初始化
- int turn = 0 ;
- turn == i //表示Ti进入临界区
- 对于Thread Ti ,代码表示如下:
do{ while(turn != i ); //如果turn不是i,死循环;直到turn是i,跳出循环 critical section //执行临界区代码 turn = j; //turn赋为j,退出循环 reminder section }while(1);
上述代码满足互斥,即不可能两个线程同时进入临界区。但不满足process,比如T1执行完进入临界区代码后,不再进入临界区程序,转去执行其他任务。而T2执行完临界区代码后,想再次进入临界区,而发现自己在退出临界区时,
把turn赋值为了1,因此再执行进入临界区代码时,由于turn=1而不是2,会执行死循环而不能进入临界区。此方法的特点就是必须T1和T2交替执行来改变turn值,才能满足process。
因此再考虑其他方法:
对于有线程0、线程1的情况:
- int flag[2]; flag[0] = flag[1] = 0
- flag[i] = 1 //如果等于1,则线程Ti进入临界区
- 对于Thread Ti,代码如下:
1 do{ 2 while (flag[j] == 1); //如果另一个进程想进来,此进程先谦让一下,自己先循环着 3 flag[i] = 1; //如果别的进程未准备,则自己赋成1,表示自己要进入临界区 4 critical section 5 flag[i] = 0; 6 reminder section 7 }while(1);
该方法没有实现互斥,如T1执行完前两条代码后,上下文切换到T2,T2执行完前两条代码后 flag[1] == flag[2] ==0 ,所以两个线程都能进入临界区,不满足互斥。
考虑将flag[i] = 1前置,代码如下
1 do{ 2 flag[i] = 1; 3 while (flag[j] == 1); 4 critical section 5 flag[i] = 0; 6 reminder section 7 }while(1);
此方法满足互斥,但可能出现死锁,
如T1执行完前两条代码后,上下文切换到T2,T2执行完前两条代码后 flag[1] == flag[2] ==1,两个进程都会进入死循环,所以两个线程都不能进入临界区。
正确的解决办法(Peterson算法)
满足进程Pi和Pj之间互斥的经典的基于软件的解决方法(1981年),Use two shared data items(用上了turn和flag)。
int turn; // 指示该谁进入临界区
boolean flag[]; // 指示进程是否准备好进入临界区
Code for ENTER_CRITICAL_SECTION
1 flag[i] = TRUE; 2 turn = j; 3 while(flag[j] && turn == j);
Code for EXIT_CRITICAL_SECTION
flag[i] = FALSE;
对于进程Pi的算法:
1 do { 2 flag[i] = TRUE; 3 turn = j; 4 while (flag[j] && turn == j); 5 CRITICAL SECTION 6 flag[i] = FALSE; 7 REMAINDER SECTION 8 } while (TRUE);
上述算法能够满足互斥、前进、有限等待三种特性。可以用反证法来证明。
更为复杂的dekker算法
dekker算法的实现如下。
flag[0] := false flag[1] := false := 0 // or 1 do { flag[i] = TRUE; while flag[j] == true { if turn != i { flag[i] := false while turn != i {} flag[i] := TRUE } } CRITICAL SECTION turn := j flag[i] = FALSE; REMAINDER SECTION } while (TRUE);
针对多进程的Eisenberg and McGuire’s Algorithm
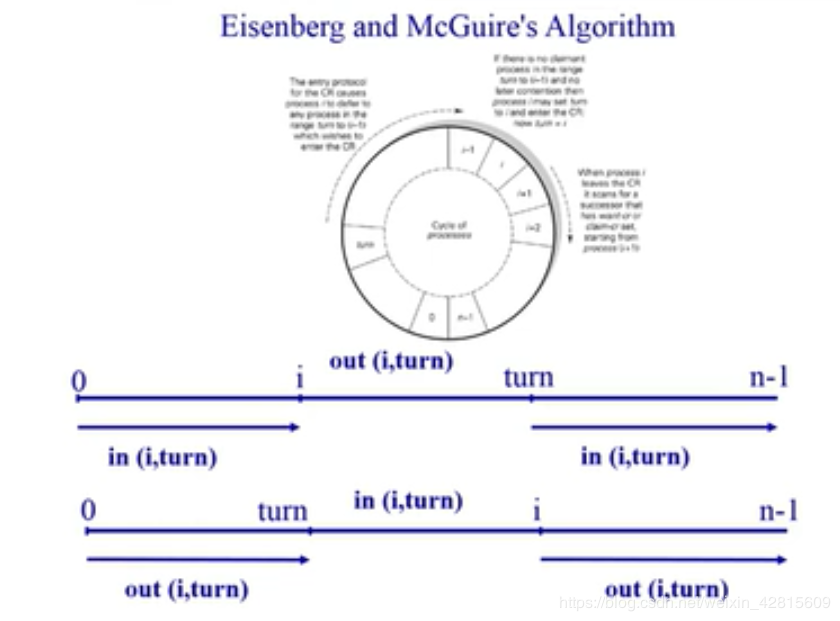
基本思路:对于i进程,如果前面有进程,那么i进程就等待;对于i后面的进程,则等待i。这整体是一种循环。
针对多进程的Bakery算法
N个进程的临界区:
- 进入临界区之前,进程接受一个数字;
- 得到的数字最小的进入临界区;
- 如果进程Pi和Pj收到相同的数字,那么如果i小于j,Pi先进入临界区,否则Pj先进入临界区;
- 编号方案总是按照枚举的增加顺序生成数字。
总结
- Dekker算法(1965):第一个针对双线程例子的正确解决方案;
- Bakery算法(Lamport 1979):针对n线程的临界区问题解决方案。
- 算法是复杂的:需要两个进程间的共享数据项;
- 需要忙等待(死循环):浪费CPU时间;
- 没有硬件保证的情况下无真正的软件解决方案:Peterson算法需要原子的LOAD和STORE指令。
方法3:更高级的抽象