4 降维

1 PCA最大方差理论

场景描述

• 对原始数据特征提取,有时会得到较高维的特征向量
• 在这些向量所处的高维空间中,含很多的冗余和噪声。
• 通过降维的方式来寻找数据内部的特性,从而提升特征表达能力,降低训练复杂度。
• Principal Components Analysis降维中最经興,有100多年
• 线性、非监督、全局的降维

问题

• 如何定义主成分?
• 从这种定义出发,如何设计目标函数使得降维达到提取主成分的目的?
• 针对这个目标函数,如何对PCA问题求解?

分析与解答

• PCA找到数据中的主成分,并用这些主成分表征原始数据,从而降维。
• 三维空间中有数据,分布在一个过原点的平面。
• 如果用自然坐标系 $x,y,z$三轴表数据,就要用三维
• 实际点只在二维平面,
  • 坐标系旋转变换使数据所在平面与 $x,y$平面重合,
  • 就可通过 $x',y'$两维表达原始数据,且没损失,
  • 完成数据降维。
• $x',y'$两轴所含的信息就是要找的主成分

 

• 高维中不像刚才这样直观地想象出数据的分布形式
• 难精确找到主成分对应的轴是哪些
• 先从最简单的二维数据来看看PCA如何工作,图4.1

 

• 图4.1(a)是二维空间中心化的数据
  • 易看出主成分所在的轴(主轴)的大致方向,
  • 图4.1(b)黄轴。
• 因为在黄轴上,数据分布更分散,意味数据在这个方向上方差大。
• 信号处理中,信号有较大方差,噪声有较小方差,信号与噪声之比称信噪比。
• 信噪比大意味着数据质量好,小意味质量差。
• 由此PCA的目标
  • 最大化投影方差,让数据在主轴上投影的方差最大

 

• 数据点 $\{\pmb{v}_1,\pmb{v}_2,\cdots,\pmb{v}_n\}$
• 中心化后为

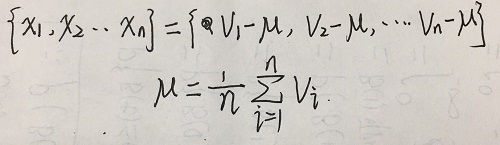
• $\pmb{x}_i$在 $\pmb{\omega}$(单位方向)上的投影坐标为 $(\pmb{x}_i,\pmb{\omega})=\pmb{x}_i^T\pmb{\omega}$
• 目标是找方向,使数据在 $\pmb{\omega}$上投影方差大。
• 投影之后均值为0(这是中心化的意义)
• 投影后的方差为

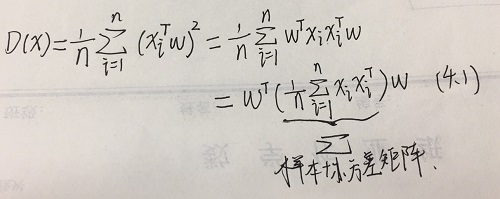
• 因此要求解一个最大化问题,
• 为

他妈的，矩阵求导还忘了

 

• 原来 $x$投影后的方差就是协方差矩阵的特征值。
• 最大的方差是协方差矩阵最大特征值,
• 最佳方向是最大特征值对应的特征向量
• 次佳方向位于最佳方向的正交空间,
  • 是第二大特征值对应的特征向量
• 至此得到几种PCA解法

 

• 样本中心化
• 求协方差矩阵
• 协方差矩阵特征值分解,从大到小
• 特征值前 $d$大对应的特征向量
  • 将 $n$维样本映射到 $d$维

• 降维后的信息占比为

总结与扩展

• PCA还可从最小回归误差得到新的目标函数。
• 但其对应的原理和求解方法等价。
• PCA是线性降维,有局限。
• 可通过核映射对PCA扩展得到核主成分分析(KPCA),
• 可通过流形映射的降维方法,如等距映射、局部线性嵌入
  • 拉普拉斯特征映射,
  • 对PCA效果不好的复杂数据集进行非线性降维

2 PCA最小平方误差理论