睡眠排序
这是那个员工写的睡眠排序,写完就被开除了hhhhh。


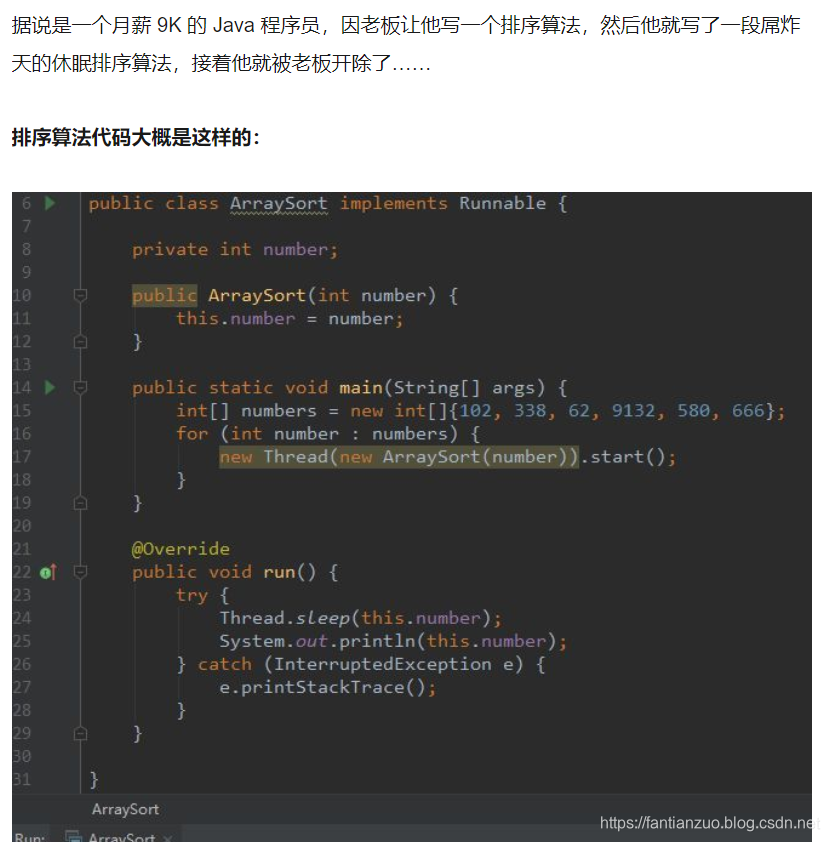
它的基本思想是:
主要是根据CPU的调度算法实现的,对一组数据进行排序,不能存在负数值,这个数是多大,那么就在线程里睡眠它的10倍再加10,不是睡眠和它的数值一样大的原因是,当数值太小时,误差太大,睡眠的时间不比输出的时间少,那么就会存在不正确的输出结果。
按道理,他的程序也没问题啊,老板为什么要开除他?应用程序中出 BUG 不是很正常的事吗?但他这种排序思维,能写出这样的隐藏 BUG 也是绝了,创造性的发明了 "休眠排序" 算法,系统里面还不知道有多少这样的坑,不开除他开除谁啊?
如果非要说一个原因,我感觉,这哥们是故意这么写的,造成查询速度较慢,之后下个迭代优化,查询速度瞬间提上来了,这可是为公司做出大贡献了,年底了,奖励个优秀个人奖.....
会死的兔子
斐波那契数列(Fibonacci sequence),又称黄金分割数列、因数学家列昂纳多·斐波那契(Leonardoda Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”。
这个例子是:刚开始,有一只兔子,这只兔子长到两岁的时候可以生一只小兔子,以后每年都可以生一只小兔子,而且兔子不会死。求第n年有几只兔子?
我们这么想:
今年的总数=去年的总数+今年的新出生的兔子,
而今年新出生的兔子=今年成熟了的兔子数量(每只成熟的兔子生一只小兔),
那今年成熟了的兔子数量又是什么呢?其实就是前年的兔子总数,因为前年的兔子,不管几岁,到今年一定成熟,可以生新兔子了。而去年的没有成熟,不能生兔子。
所以今年的总数=去年的总数+前年的总数。
F(n)=F(n-1)+F(n-2)。
这个数列就是1、1、2、3、5、8、13、21、34、……
在数学上,斐波那契数列以如下被以递推的方法定义:F(1)=1,F(2)=1, F(n)=F(n-1)+F(n-2)(n>=3,n∈N*)在现代物理、准晶体结构、化学等领域,斐波纳契数列都有直接的应用,为此,美国数学会从1963年起出版了以《斐波纳契数列季刊》为名的一份数学杂志,用于专门刊载这方面的研究成果。
解题也非常容易
解法一:完全抄定义
def f(n):
if n==1 or n==2:
return 1
return f(n-1)+f(n-2)分析一下,为什么说递归效率很低呢?咱们来试着运行一下就知道了:
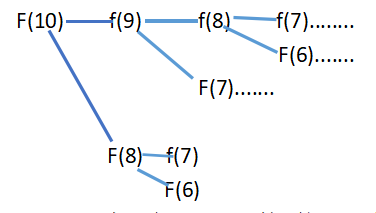
比如想求f(10),计算机里怎么运行的?
想算出f(10),就要先算出F(9),
想算出f(9),就要先算出F(8),
想算出f(8),就要先算出F(7),
想算出f(7),就要先算出F(6)……
兜了一圈,我们发现,有相当多的计算都重复了,比如红框部分:
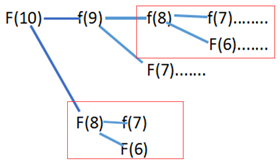
那如何解决这个问题呢?问题的原因就在于,我们算出来某个结果,并没有记录下来,导致了重复计算。那很容易想到如果我们把计算的结果全都保存下来,按照一定的顺序推出n项,就可以提升效率
解法2:
def f1(n):
if n==1 or n==2:
return 1
l=[0]*n #保存结果
l[0],l[1]=1,1 #赋初值
for i in range(2,n):
l[i]=l[i-1]+l[i-2] #直接利用之前结果
return l[-1]可以看出,时间o(n),空间o(n)。
继续思考,既然只求第n项,而斐波那契又严格依赖前两项,那我们何必记录那么多值浪费空间呢?只记录前两项就可以了。
解法3:
def f2(n):
a,b=1,1
for i in range(n-1):
a,b=b,a+b
return a但是就有这么一个问题:兔子也会死
出生到死亡只有三年,即n年出生,n+3年死去。
出生一年以后可以生育,也就是n+1年开始生育,一年可以生一只宝宝。
如果你硬要推今年的总数,你会发现相当困难。
这时我们换一个思路:
定义f(n)为第n年新出生的动物个数,则f(n)=f(n-1)+f(n-2),前两项为1,而每年的总数也就是三项求和而已。
每年出生的数量为1,1,2,3,5,8,13,21
每年总数就是1,2,4,10,16,26,42
发现依旧是前两项加起来。
所以当我们按老思路解不出新的变形题,这时不妨换个思路,可能会有奇效,你想到了吗?
矩阵快速幂
还是上面的斐波那契数列问题(兔子不会死),这种递推的题,一般无法突破O(N)时间的魔咒,但是我们可以利用矩阵快速幂的方法写出O(logN)的方法,是不是很神奇?

public static int[][] matrixPower(int[][] m, int p) {
int[][] res = new int[m.length][m[0].length];
for (int i = 0; i < res.length; i++) {
res[i][i] = 1;
}
int[][] tmp = m;
for (; p != 0; p >>= 1) {
if ((p & 1) != 0) {
res = muliMatrix(res, tmp);
}
tmp = muliMatrix(tmp, tmp);
}
return res;
}
public static int[][] muliMatrix(int[][] m1, int[][] m2) {
int[][] res = new int[m1.length][m2[0].length];
for (int i = 0; i < m1.length; i++) {
for (int j = 0; j < m2[0].length; j++) {
for (int k = 0; k < m2.length; k++) {
res[i][j] += m1[i][k] * m2[k][j];
}
}
}
return res;
} public static int f3(int n) {
if (n < 1) {
return 0;
}
if (n == 1 || n == 2) {
return 1;
}
int[][] base = { { 1, 1 }, { 1, 0 } };
int[][] res = matrixPower(base, n - 2);
return res[0][0] + res[1][0];
}值得思考的是,当我们一项一项的一维计算到达维度极限时,提高一个维度的计算就突破了时间极限,那么是否有三维的计算的解法?
摔手机/摔鸡蛋
如果对算法感兴趣的朋友,可能会知道下面这道题:
leetcode的hard难度(我认为应该出一个顶级难度):
你将获得 K 个鸡蛋,并可以使用一栋从 1 到 N 共有 N 层楼的建筑。
每个蛋的功能都是一样的,如果一个蛋碎了,你就不能再把它掉下去。
你知道存在楼层 F ,满足 0 <= F <= N 任何从高于 F 的楼层落下的鸡蛋都会碎,从 F 楼层或比它低的楼层落下的鸡蛋都不会破。
每次移动,你可以取一个鸡蛋(如果你有完整的鸡蛋)并把它从任一楼层 X 扔下(满足 1 <= X <= N)。
你的目标是确切地知道 F 的值是多少。
无论 F 的初始值如何,你确定 F 的值的最小移动次数是多少?
示例 1:
输入:K = 1, N = 2
输出:2
解释:鸡蛋从 1 楼掉落。如果它碎了,我们肯定知道 F = 0 。
否则,鸡蛋从 2 楼掉落。如果它碎了,我们肯定知道 F = 1 。
如果它没碎,那么我们肯定知道 F = 2 。
因此,在最坏的情况下我们需要移动 2 次以确定 F 是多少。
蓝桥杯:
x星球的居民脾气不太好,但好在他们生气的时候唯一的异常举动是:摔手机。
各大厂商也就纷纷推出各种耐摔型手机。x星球的质监局规定了手机必须经过耐摔测试,并且评定出一个耐摔指数来,之后才允许上市流通。
x星球有很多高耸入云的高塔,刚好可以用来做耐摔测试。塔的每一层高度都是一样的,与地球上稍有不同的是,他们的第一层不是地面,而是相当于我们的2楼。
如果手机从第7层扔下去没摔坏,但第8层摔坏了,则手机耐摔指数=7。
特别地,如果手机从第1层扔下去就坏了,则耐摔指数=0。如果到了塔的最高层第n层扔没摔坏,则耐摔指数=n
为了减少测试次数,从每个厂家抽样3部手机参加测试。
某次测试的塔高为1000层,如果我们总是采用最佳策略,在最坏的运气下最多需要测试多少次才能确定手机的耐摔指数呢?
请填写这个最多测试次数。
注意:需要填写的是一个整数,不要填写任何多余内容
答案19
问法不同,但是实际上是一个问题。
读完题后,我们追求的不是要写出得数(至少对于本博客是不够的),而是用代码实现方法,并思考是否可以优化。
其实本题的方法是非常多种多样的。非常适合锻炼思维。
我们把问题扩展到n个手机来思考。
手机k个,楼n层,最终结果M次。
时空复杂度目录
暴力: O(N!)
DP: O(N*N*K) O(N*K)
压空间: O(N*N*K) O(N)
四边形不等式优化 O(N*N)
换思路: O(K*M)
最优: O(K*M) O(N)
文末有测试,大家可以去直观感受一下各方法运行的效率
二分
容易想到二分思路:不断二分范围,取中点,测验是否会摔坏,然后缩小一半范围,继续尝试,很显然,答案为logN(2为底)
但是,二分得出的答案是不对的。注意:我们要保证在都手机摔完之前,能确定耐摔指数到底是多少。
举例:
我们在500楼摔坏了,在250楼摔,又坏了。接下来,我们只能从1楼开始一层一层试
因为如果我们在125层摔坏了,就没有手机可以用,也就是永远都测不出来,而这是不被允许的。其实我们连测第2层都不敢测,因为在第2层摔坏了,我们就无法知道手机在第一层能否被摔坏。所以只有一部手机时,我们只敢从第一层开始摔。
尝试较优的策略
既然二分是不对的,我们继续分析:摔手机的最优策略到底是如何的。
只有一部手机时,我们只敢从第一层开始摔。
有两部手机的时候,我们就敢隔层摔了,因为一部手机坏了,我们还有另一部来继续试。
这时就有点意思了,我们分析情况:
情况1)假设我们第一部手机在i层摔坏了,然后最坏情况还要试多少次?这时我们还剩一部手机,所以只敢一层一层试,最坏情况要试到i-1层,共试了i次。
情况2)假设我们第一部手机在i层试了,但是没摔坏,然后最坏情况还要试多少次?(这时发现算情况2时依旧是相似的问题,确定了可以用递归来解。)
最优解(最小值)是决策后两种情况的最差情况(最大值),我们的本能感觉应该就是让最差情况好一点,让最好情况差一点,这样比较接近正确答案。比如两部手机,一百层,我们可以在50层摔,没坏,这一次就很赚,我们没摔坏手机还把范围缩小了50层。如果坏了,就比较坑了,我们要从1试到50。虽然可能缩小一半,但是最坏情况次数太多,所以肯定要从某个低于五十的层开始尝试。
(以上几行是为了让读者理解决策,下面正文分析)
归纳表达式
假设我们的楼一共n层,我们的i可以取1-n任意值,有很多种可能的决策,我们的最小值设为f(n,k),n代表楼高(范围为1-100或101-200其实都一样),k代表手机数.
我们假设的决策是在第i楼扔
对于情况一,手机少了一部,并且我们确定了范围,一定在第i楼以下,所以手机-1,层数为i-1,这时f(n,k)=f(i-1,k-1).+1
对于情况二,手机没少,并且我们确定了范围,一定在第i楼之上,所以手机数不变,而层数-i层,这时f(n,k)=f(n-i,k).+1
归纳出
f(n,k)=min( max(f(i-1,k-1) ,f(n-i,k) ) i取1-n任意数 )+1
简单总结:怎么确定第一个手机在哪扔?每层都试试,哪层的最坏情况(max)最好(min),就去哪层扔。
写出暴力递归
按照分析出来的表达式,我们可以写出暴力递归:
public static int solution1(int nLevel, int kChess) {
if (nLevel == 0) {
return 0;
}//范围缩小至0
if (kChess == 1) {
return nLevel;
}//每层依次试
int min = Integer.MAX_VALUE;//取不影响结果的数
for (int i = 1; i != nLevel + 1; i++) {
//尝试所有决策,取最优
min = Math.min(
min,
Math.max(Process1(i - 1, kChess - 1),Process1(nLevel - i, kChess)));
}
return min + 1;//别忘了加上本次
}改为动态规划
具体思路如下
https://blog.csdn.net/hebtu666/article/details/79912328
public static int solution2(int nLevel, int kChess) {
if (kChess == 1) {
return nLevel;
}
int[][] dp = new int[nLevel + 1][kChess + 1];
for (int i = 1; i != dp.length; i++) {
dp[i][1] = i;
}
for (int i = 1; i != dp.length; i++) {
for (int j = 2; j != dp[0].length; j++) {
int min = Integer.MAX_VALUE;
for (int k = 1; k != i + 1; k++) {
min = Math.min(min,
Math.max(dp[k - 1][j - 1], dp[i - k][j]));
}
dp[i][j] = min + 1;
}
}
return dp[nLevel][kChess];
}压缩空间
我们发现,对于状态转移方程,只和上一盘排的dp表和左边的dp表有关,所以我们不需要把值全部记录,用两个长度为n的数组不断更新即可(具体对dp压缩空间的思路,也是很重要的,我在其它文章中有提过,在这里就不写了)
public static int solution3(int nLevel, int kChess) {
if (kChess == 1) {
return nLevel;
}
int[] preArr = new int[nLevel + 1];
int[] curArr = new int[nLevel + 1];
for (int i = 1; i != curArr.length; i++) {
curArr[i] = i;
}//初始化
for (int i = 1; i != kChess; i++) {
//先交换
int[] tmp = preArr;
preArr = curArr;
curArr = tmp;
//然后打新的一行
for (int j = 1; j != curArr.length; j++) {
int min = Integer.MAX_VALUE;
for (int k = 1; k != j + 1; k++) {
min = Math.min(min, Math.max(preArr[k - 1], curArr[j - k]));
}
curArr[j] = min + 1;
}
}
return curArr[curArr.length - 1];
}四边形不等式优化
四边形不等式是一种比较常见的优化动态规划的方法
定义:如果对于任意的a1≤a2<b1≤b2,有m[a1,b1]+m[a2,b2]≤m[a1,b2]+m[a2,b1],那么m[i,j]满足四边形不等式。
对s[i,j-1]≤s[i,j]≤s[i+1,j]的证明:
设mk[i,j]=m[i,k]+m[k,j],s[i,j]=d
对于任意k<d,有mk[i,j]≥md[i,j](这里以m[i,j]=min{m[i,k]+m[k,j]}为例,max的类似),接下来只要证明mk[i+1,j]≥md[i+1,j],那么只有当s[i+1,j]≥s[i,j]时才有可能有mk[i+1,j]≥md[i+1,j]
(mk[i+1,j]-md[i+1,j])-(mk[i,j]-md[i,j])
=(mk[i+1,j]+md[i,j])-(md[i+1,j]+mk[i,j])
=(m[i+1,k]+m[k,j]+m[i,d]+m[d,j])-(m[i+1,d]+m[d,j]+m[i,k]+m[k,j])
=(m[i+1,k]+m[i,d])-(m[i+1,d]+m[i,k])
∵m满足四边形不等式,∴对于i<i+1≤k<d有m[i+1,k]+m[i,d]≥m[i+1,d]+m[i,k]
∴(mk[i+1,j]-md[i+1,j])≥(mk[i,j]-md[i,j])≥0
∴s[i,j]≤s[i+1,j],同理可证s[i,j-1]≤s[i,j]
证毕
通俗来说,
优化策略1)我们在求k+1手机n层楼时,最后发现,第一个手机在m层扔导致了最优解的产生。那我们在求k个手机n层楼时,第一个手机的策略就不用尝试m层以上的楼了。
优化策略2)我们在求k个手机n层楼时,最后发现,第一个手机在m层扔导致了最优解的产生。那我们在求k个手机n+1层楼时,就不用尝试m层以下的楼了。
public static int solution4(int nLevel, int kChess) {
if (kChess == 1) {
return nLevel;
}
int[][] dp = new int[nLevel + 1][kChess + 1];
for (int i = 1; i != dp.length; i++) {
dp[i][1] = i;
}
int[] cands = new int[kChess + 1];
for (int i = 1; i != dp[0].length; i++) {
dp[1][i] = 1;
cands[i] = 1;
}
for (int i = 2; i < nLevel + 1; i++) {
for (int j = kChess; j > 1; j--) {
int min = Integer.MAX_VALUE;
int minEnum = cands[j];
int maxEnum = j == kChess ? i / 2 + 1 : cands[j + 1];
//优化策略
for (int k = minEnum; k < maxEnum + 1; k++) {
int cur = Math.max(dp[k - 1][j - 1], dp[i - k][j]);
if (cur <= min) {
min = cur;
cands[j] = k;//最优解记录层数
}
}
dp[i][j] = min + 1;
}
}
return dp[nLevel][kChess];
}注:对于四边形不等式的题目,比赛时不需要严格证明
通常的做法是打表出来之后找规律,然后大胆猜测,显然可得。(手动滑稽)
换一种思路
有时,最优解并不是优化来的。
当你对着某个题冥思苦想了好久,无论如何也不知道怎么把时间优化到合理范围,可能这个题的最优解就不是这种思路,这时,试着换一种思路思考,可能会有奇效。
(比如训练时一道贪心我死活往dp想,肝了两个小时以后,不主攻这个方向的队友三分钟就有贪心思路了,泪目,不要把简单问题复杂化)
我们换一种思路想问题:
原问题:n层楼,k个手机,最多测试次数
反过来看问题:k个手机,扔m次,最多能确定多少层楼?
我们定义dp[i][j]:i个手机扔j次能确定的楼数。
分析情况:依旧是看第一部手机在哪层扔的决策,同样,我们的决策首先要保证能确定从1层某一段,而不能出现次数用完了还没确定好的情况。以这个为前提,保证了每次扔的楼层都是最优的,就能求出结果。
依旧是取最坏情况:min(情况1,情况2)
情况1)第一个手机碎了,我们就需要用剩下的i-1个手机和j-1次测试次数往下去测,dp[i-1][j-1]。那我们能确定的层数是无限的,因为本层以上的无限层楼都不会被摔坏。dp[i-1][j-1]+无穷=无穷
情况2)第一个手机没碎,那我们就看i个手机扔j-1次能确定的楼数(向上试)+当前楼高h
归纳表达式,要取最差情况,所以就是只有情况2:dp[i][j]=dp[i-1][j-1]+h
那这个h到底是什么呢?取决于我敢从哪层扔。因为次数减了一次,我们还是要考虑i个球和j-1次的最坏情况能确定多少层,我才敢在层数+1的地方扔。(这是重点)
也就是dp[i][j-1]的向上一层:h=dp[i][j-1]+1
总:min(情况1,情况2)=min(无穷,dp[i-1][j-1]+dp[i][j-1]+1)=dp[i-1][j-1]+dp[i][j-1]+1
这是解决k个手机,扔m次,最多能确定多少层楼?
原问题是n层楼,k个手机,最多测试次数。
所以我们在求的过程中,何时能确定的层数大于n,输出扔的次数即可
最优解
我们知道完全用二分扔需要logN+1次,这也绝对是手机足够情况下的最优解,我们做的这么多努力都是因为手机不够摔啊。。。。所以当我们的手机足够用二分来摔时,直接求出logN+1即可。
当然,我们求dp需要左边的值和左上的值:

依旧可以压缩空间,从左往右更新,previous记录左上的值。
求自己时也要注意记录,否则更新过后,后面的要用没更新过的值(左上方)就找不到了。
记录之后,求出当前数值,把记录的temp值给了previous即可。
public static int solution5(int nLevel, int kChess) {
int bsTimes = log2N(nLevel) + 1;
if (kChess >= bsTimes) {
return bsTimes;
}
int[] dp = new int[kChess];
int res = 0;
while (true) {
res++;//压缩空间记得记录次数
int previous = 0;
for (int i = 0; i < dp.length; i++) {
int tmp = dp[i];
dp[i] = dp[i] + previous + 1;
previous = tmp;
if (dp[i] >= nLevel) {
return res;
}
}
}
}
public static int log2N(int n) {
int res = -1;
while (n != 0) {
res++;
n >>>= 1;
}
return res;
}测试:
暴力: O(N!)
DP: O(N*N*K) O(N*K)
压空间: O(N*N*K) O(N)
四边形不等式优化 O(N*N)
最优: O(K*M) O(N)
long start = System.currentTimeMillis();
solution1(30, 2);
long end = System.currentTimeMillis();
System.out.println("cost time: " + (end - start) + " ms");
start = System.currentTimeMillis();
solution2(30, 2);
end = System.currentTimeMillis();
System.out.println("cost time: " + (end - start) + " ms");
start = System.currentTimeMillis();
solution3(30, 2);
end = System.currentTimeMillis();
System.out.println("cost time: " + (end - start) + " ms");
start = System.currentTimeMillis();
solution4(30, 2);
end = System.currentTimeMillis();
System.out.println("cost time: " + (end - start) + " ms");
start = System.currentTimeMillis();
solution5(30, 2);
end = System.currentTimeMillis();
System.out.println("cost time: " + (end - start) + " ms");
/*
结果:
cost time: 7043 ms
cost time: 0 ms
cost time: 0 ms
cost time: 0 ms
cost time: 0 ms
*/暴力时间实在是太久了,只测一个30,2
后四种方法测的大一些(差点把电脑测炸了,cpu100内存100):
solution(100000, 10):
solution2 cost time: 202525 ms
solution3 cost time: 38131 ms
solution4 cost time: 11295 ms
solution5 cost time: 0 ms
感受最优解的强大:
solution5(1000 000 000,100):0 ms
solution5(1000 000 000,10):0 ms
最优解永远都是0 ms,我也是服了。。
对比方法,在时间复杂度相同的条件下,空间复杂度一样会影响时间,因为空间太大的话,申请空间是相当浪费时间的。并且空间太大电脑会炸,所以不要认为空间不重要。