欧拉问题

欧拉回路

定义：

• 给定一张图，如何求出一条经过每条边恰好一次的回路。（行遍所有边）
• 必要条件：
• 有向图
  1.给定的图是一个强连通分量(基图是连通)。

基图就是把有向边变为无向边。

2.每个点的入度等于出度（进来了一定要出去）。
3.不难发现这两个条件其实也是充分的。

• 无向图
  1.每个点的度数都是偶数（even）
  2.图是连通的

圈套圈算法：

文字描述：

• 任选一个起点，从起点开始 $dfs$，每条边只能被走一遍，当没有边可以走的时候把 $x$压入答案队列中。
• 最后的答案就是反着的欧拉回路。

解释：

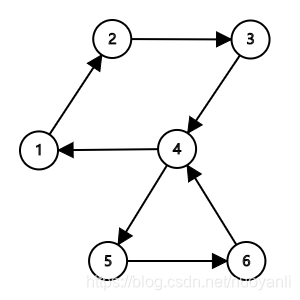
$dfs(1)-dfs(2)-dfs(3)-dfs(4)-dfs(1)$，1无路可走，把1压入答案队列。
$dfs(4)-dfs(5)-dfs(6)-dfs(4)$，4无路可走，把4压入答案队列。
依次求得：1 4 6 5 4 3 2 1
所以1 2 3 4 5 6 4 1位一条欧拉回路。

• 原理：
  理想状态下就是 $dfs$一个环没有分支，当存在分支又是连通分量（前提是欧拉图），那么就可以跑完这个环再去遍历下一个环，依次回溯。(符合 $fleury$算法）
• 复杂度： $O(n)$

代码实现：

无向图：

/*
无向图的欧拉回路
邻接矩阵存图
*/
#include<cstdio>
#include<cstring>
const int N=1e3+10;
int ans[N];//存放点的顺序
int book[N];//表示每个点的度数
int map[N][N];
int top,n,m;
void dfs(int x) {
	for(int i=1; i<=n; i++) {
		if(map[x][i]) {
			map[x][i]--;
			map[i][x]--;
			dfs(i);
		}
	}
	ans[top++]=x;//放入队列中
}
void fleury(int x) {
	top=0;
	dfs(x);
}
void Print_road() { //输出路径
	for(int i=top-1; i>=0; i--) {
		printf("%d",ans[i]);
		if(i) {
			printf("-->");
		}
	}
	puts("");
}
int main() {
	int x;
	while(~scanf("%d %d",&n,&m)) { //共有n个点，m个边   //欧拉回路所有边只走一次
		memset(book,0,sizeof(book));
		memset(map,0,sizeof(map));
		for(int i=0; i<m; i++) {
			int u,v;
			scanf("%d %d",&u,&v);
			book[u]++;
			book[v]++;
			map[u][v]=map[v][u]=1;
		}//构建数组链表
		x=1;
		int cnt=0;
		for(int i=1; i<=n; i++) {
			if(book[i]&1) {
				cnt++;
				x=i;
			}
		}
		if(!cnt||cnt==2) { //找出x
			fleury(x);
			Print_road();
		} else {
			printf("不存在欧拉回路\n");
			continue;
		}
	}
}

有向图：

/*
fleury 有向边
用了邻接表实现
*/

#include<cstdio>
#include<cstring>
const int N=1e3+10;
struct Node {
	int v;
	int next,index,flag;
} node[N];
int head[N];//存放每个u节点的第一个指向
int ans[N];//存放点的顺序
int rbook[N],cbook[N];//表示每个点的度数
int top;
void dfs(int x) {
	int to;
	to=head[x];
	while(to!=-1) {
		if(node[to].flag) {
			node[to].flag=0;
			dfs(node[to].v);
		}
		to=node[to].next;
	}
	ans[top++]=x;
}
void fleury(int x) {
	top=0;
	dfs(x);
}
void Print_road() { //输出路径
	for(int i=top-1; i>=0; i--) {
		printf("%d",ans[i]);
		if(i)
			printf("-->");
	}
	puts("");
}
int main() {
	int n,m,x;
	while(~scanf("%d %d",&n,&m)) { //共有n个点，m个边   //欧拉回路所有边只走一次
		memset(rbook,0,sizeof(rbook));
		memset(cbook,0,sizeof(cbook));
		memset(head,-1,sizeof(head));

		for(int i=0; i<m; i++) {
			int u,v;
			scanf("%d %d",&u,&v);
			cbook[u]++;
			rbook[v]++;
			node[i].v=v;
			node[i].flag=1;
			node[i].index=i;
			node[i].next=head[u];
			head[u]=i;
		}//构建数组链表
		x=1;
		int cnt=0;
		for(int i=1; i<=n; i++) {
			if(rbook[i]!=cbook[i]) { //计算出度不等于入读的个数
				cnt++;
				if(cbook[i]>rbook[i])//因为总的出度与总的入度个数是相同的，所有必有一大一小
					x=i;
			}
		}
		if(!cnt||cnt==2) { //找出x
			fleury(x);
			Print_road();
		} else {
			printf("不存在欧拉回路\n");
			continue;
		}
	}
	return 0;
}

欧拉路径

定义：

经过所有边。相当于在欧拉回路里面去掉一条边。

• 必要条件：
  1.只有两个度数为奇数的点。
  2.连通。