定义
后缀自动机(\(\text{Suffix Automaton}\),简称 \(\text{SAM}\))。对于一个字符串 \(S\),它对应的后缀自动机是一个最小的确定有限状态自动机(\(\text{DFA}\)),接受且只接受 \(S\) 的后缀。
比如对于字符串 \(S = \underline{aabbabd}\),它的后缀自动机是
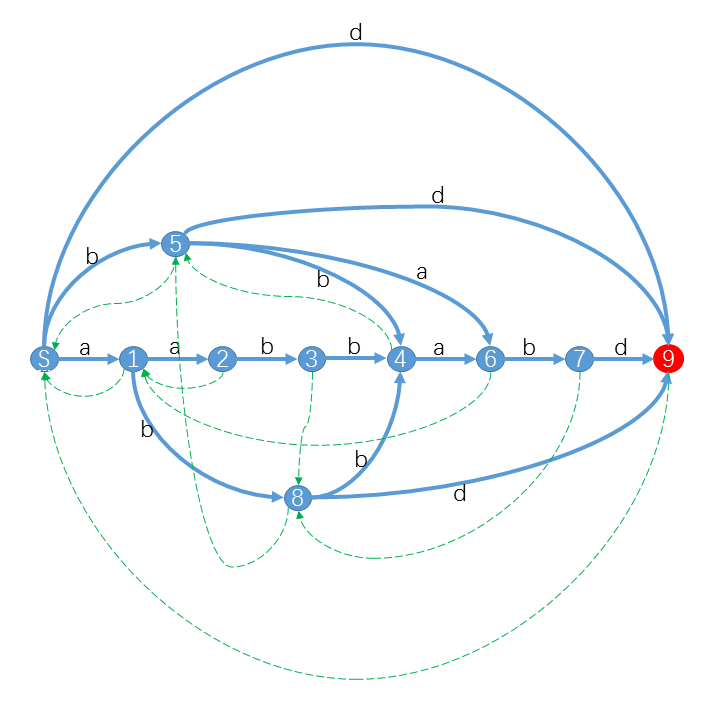
其中\(\textcolor[rgb]{1,0,0}{红色状态}\)是终结状态。你可以发现对于 \(S\) 的后缀,我们都可以从 \(S\) 出发沿着字符标示的路径(\(\textcolor[rgb]{0,0,1}{蓝色实线}\))转移,最终到达终结状态。
特别的,对于 \(S\) 的子串,最终会到达一个合法状态。而对于其他不是 \(S\) 子串的字符串,最终会“无路可走”。
\(\text{SAM}\) 本质上是一个 \(\text{DFA}\),\(\text{DFA}\) 可以用一个五元组 <字符集,状态集,转移函数、起始状态、终结状态集>来表示。至于那些 \(\textcolor[rgb]{0,1,0}{绿色虚线}\)虽然不是 \(\text{DFA}\) 的一部分,但却是 \(\text{SAM}\) 的重要部分,有了这些链接 \(\text{SAM}\) 是如虎添翼,这些后面将再细讲。
下面先介绍对于一个给定的字符串 \(S\) 如何确定它对应的 状态集 和 转移函数 。
SAM 的状态集 (States)
首先先介绍一个概念 子串的结束位置集合 \(endpos\)
对于 \(S\) 的一个子串 \(s\),\(endpos(s) = s\) 在 \(S\) 中所有出现的结束位置集合。
以字符串 \(S = \underline{aabbabd}\) 为例
| 状态 | 子串 | \(endpos\) |
|---|---|---|
| \(S\) | \(\varnothing\) | \(\{0,1,2,3,4,5,6\}\) |
| \(1\) | \(a\) | \(\{{1,2,5}\}\) |
| \(2\) | \(aa\) | \(\{2\}\) |
| \(3\) | \(aab\) | \(\{3\}\) |
| \(4\) | \(aabb,abb,bb\) | \(\{4\}\) |
| \(5\) | \(b\) | \(\{3,4,6\}\) |
| \(6\) | \(aabba,abba,bba,ba\) | \(\{5\}\) |
| \(7\) | \(aabbab,abbab,bbab,bab\) | \(\{6\}\) |
| \(8\) | \(ab\) | \(\{3,6\}\) |
| \(9\) | \(aabbabd,abbabd,bbabd,babd,abd,bd,d\) | \(\{7\}\) |