快速傅里叶变换|快速数论变换

FFT——快速傅里叶变换

什么是FFT

\(FFT\)全称(\(Fast \ Fourier \ Transformation\))，中文名：快速傅里叶离散变换。

这个名字听起来很高级，实际上也很高级，它是\(DFT\)和\(IDFT\)的加速版本，用于加速多项式乘法。

• 接下来我们把某个多项式记为“大写字母+元素”，如多项式：

\(A(x)=a_nx^n+a_{n-1}x^{n-1}+…+a_2x^2+a_1x^1+a_0\)

\(B(x)=b_mx^m+b_{m-1}x^{m-1}+…+b_2x^2+b_1x^1+b_0\)

你也可以理解为\(A/B\)是关于\(x\)的函数

现在，我们要求\(A(x)*B(x)\)，即两个多项式的乘积(卷积)，那么我们很容易想到的就是\(O(N^2)\)的做法：把每一项依次分别相乘再相加。

\[\sum^{n+m-1}_{i=0}(\sum^{i}_{j=0}a_i*b_{i-j})*x^i\]

这样的时间复杂度明显不尽人意，那么\(FFT\)就是把这种算式计算优化到\(NlogN\)的算法。

---

前置知识

• 复数

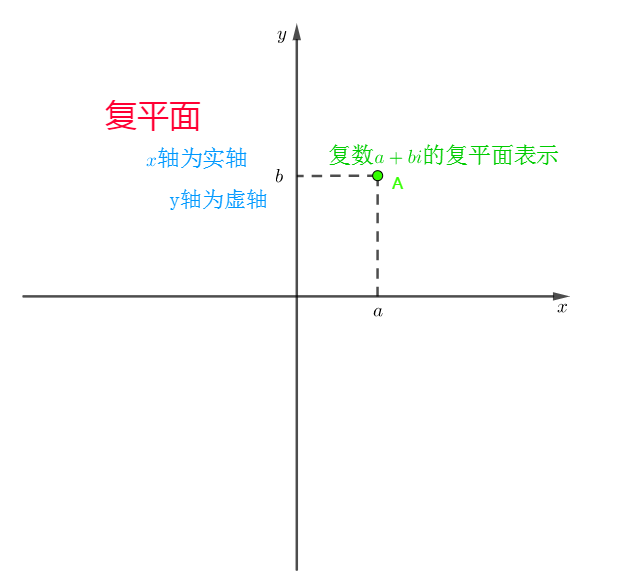
我们定义虚数 \(i\)， 且 \(i^2 = -1\)，即 \(i = \sqrt {-1}\)，那么复数就形如 \(a+bi\)，\(i\) 是一个虚数单位，\(a\) 叫做复数的实部， \(b\) 叫做复数的虚部，那么 \(a+bi\) 在复平面（高中会讲）可以类似于平面直角坐标系，表示为点 \((a, b)\)。

复数的运算法则

1. 加法：实部和虚部分别相加。

2. 减法：实部和虚部分别相减。

3. 乘法：像一次多项式一样相乘。

4. 除法：分子分母同乘分母的共轭。

共轭：两个复数实部相同，虚部相反。

上面除法分子分母同乘分母的共轭，把分母有理化成实数。

    struct complex { //复数 
        long double a, b;
        complex() { a = b = 0;}
        //重载复数四则运算 
        complex operator + (const complex x) const {
            complex temp;
            temp.a = a + x.a;
            temp.b = b + x.b;
            return temp; 
        }

        complex  operator - (const complex x) const {
            complex temp;
            temp.a = a - x.a;
            temp.b = b - x.b;
            return temp; 
        }

        complex operator * (const complex x) const {
            complex temp;
            temp.a = a * x.a - b * x.b;
            temp.b = a * x.b + b * x.a;
            return temp; 
        }

        complex operator / (const complex x) const {
            double div = x.a * x.a + x.b * x.b;
            complex temp;
            temp.a = (a * x.a + b * x.b) / div;
            temp.b = (b * x.a - a * x.b) / div;
            return temp; 
        }
    };

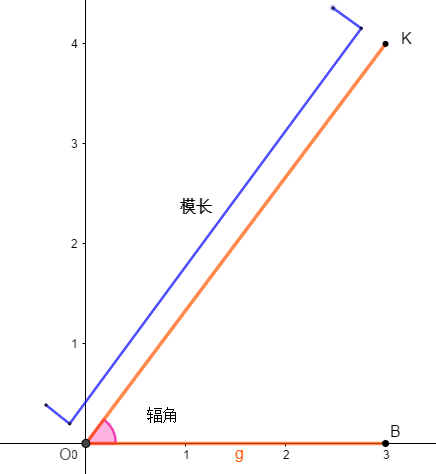
这边大家直接记一个重要结论：

复数相乘，辐角相加，模长相乘。

---

单位根

对于复数\(w\),若整数 \(n\) 满足 \(w^n=1\)，则称 \(w\) 是 \(n\) 次单位根。

扔个单位圆：

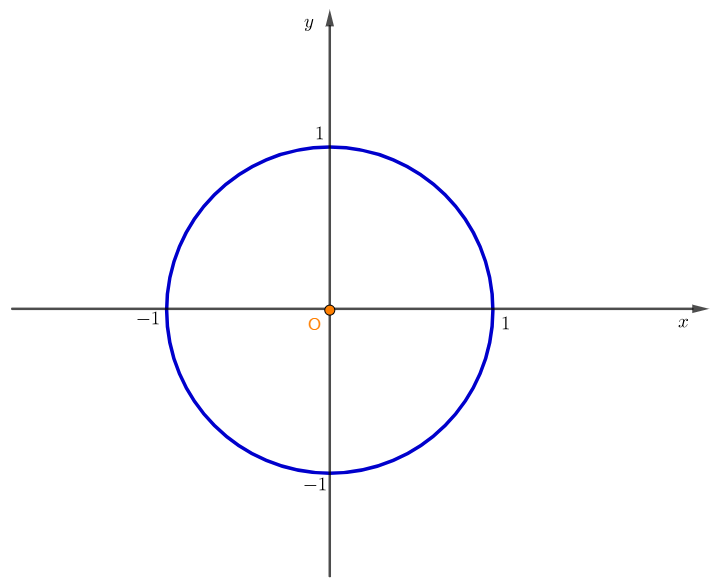
为什么扔个单位圆呢？因为单位圆上任意一点到原点的距离，即模长都为\(1\)。

那么，对于一个复数，只有模长为\(1\)的复数才有可能成为\(n\)次单位根!

现在，我们在复平面上把复数锁定在了这个单位圆上。

设复数\(w\)模长为\(q\)，其幅角为\(mπ\)，\(m\)为\([0,2]\)间实数，那么，其\(n\)次方幅角为\(nmπ\)。

则有\(nmπ=kπ,k∈N\)，即\(nm=k\)。

1. 若\(k=0\),因为\(n>0\)，所以方程有且只有\(m=0\)一解。

2. 若\(k>0\)，则\(k=1,2,3,…\)，易知\(m\)有\(n-1\)个不重解

综上，复数\(w\)的\(n\)次单位根有\(n\)个。

并且，复数的\(n\)次单位根\(n\)等分单位圆。

单位根的书写：

单位根用符号\(ω\)表示，从1开始，沿单位圆逆时针把单位根从\(0\)开始标号。

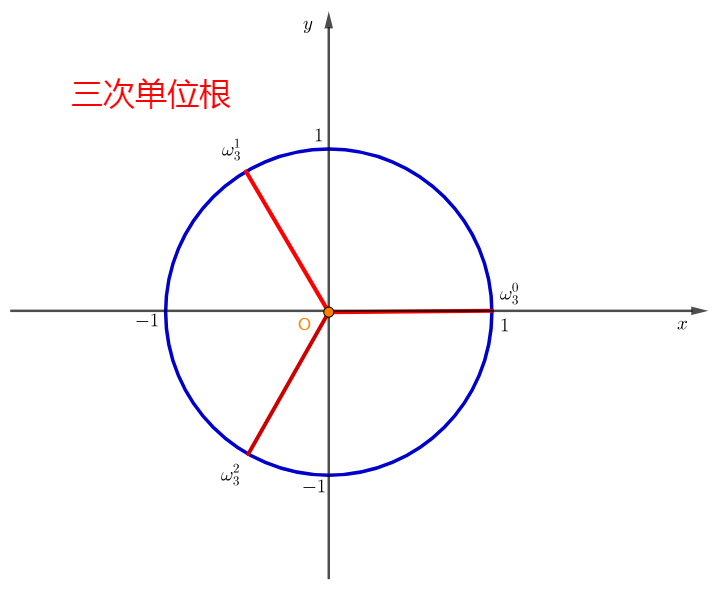
然后单位根还有个神奇的东西\(ω^{k}_{n}=ω_{n}^{k\mod n}\)

单位根的性质

1. 对于任意\(n\)，\(ω_n^0=1\)。

2. \(ω_n^k=(ω_n^1)^k\)。

3. \((ω_n^m)^k=(ω_n^k)^m\)

4. \(ω_n^i*ω_n^j=ω_{n}^{i+j}\)。

5. \(ω_{2n}^{2m}=ω_n^m\)。

6. 若 \(2 \mid n\)，\(ω_n^{m+\frac{n}{2}}=-ω_n^m\)

---

多项式的表达方法

1. 系数表达法：这个如同我们上面写的多项式即为系数表达法。

2. 点值表达法

定义多项式\(F(x)\)：

我们知道，\(1\)个n元一次方程最少需要\(n\)个式子求解，而我们把系数表达\(F(x)\)抽象为一个函数\(F(x)\)，那么这个函数至少需要\(n+1\)个点确定下来，那么我们任取\(n+1\)个不同的数构成集合\(U={k_1,k_2,…,k_{n+1}}\)，对\(F(x)\)分别求值得到一个新的集合，那么将两个集合合并成点集，有：

\[T={(k_1,F(k_1)),k_2,F(k_2),…,(k_{n+1},F(n+1))}\]

这便是\(F(x)\)的点值表达式，并且，点值表达法下的乘法运算更加简单：

多项式\(P,Q\)分别取点\((x,y_1)\)和\((x,y_2)\)，则\(P*Q\)可得到点\((x,y_1*y_2)\)。令\(S=P*Q\)，则\(C(x_i)=y_{1_i}*y_{2_i}\)。

可见，点值表达法下，多项式乘法是\(O(N)\)的。

• （补充）乘法本质：卷积

根据我们上面暴力计算\(A(x)*B(x)\)，不妨设\(C=A*B\)，那么：

\(C[k]=\sum^{k}_{i=0}A[i]B[k-i]\)

\(A[i],B[k-1]\)分别为\(A\)中\(x^i\)的系数和\(B\)中\(x^{k-i}\)的系数，那么我们知道：\(x^i*x^{k-i}=x^k\)，故所有的\(x^i*x^{k-i}\)的系数对\(x\)的次项系数均有贡献，需要累加。

那么就可以写成：\(C[k]=\sum\limits_{i+j=k}A[i]B[j]\)

那么形如\(C[k]=\sum\limits_{i⊕j=k}A[i]B[j]\)(\(⊕\)为某种运算)的式子称为卷积。

那么，多项式的乘法就是对于加法的卷积。

我们仍然可以对多项式相乘的模板打个暴力：

    #include<bits/stdc++.h>
    using namespace std;

    const int SIZE = 1e6 + 10;

    long long A[SIZE], B[SIZE], C[SIZE];
    int n, m;

    int main() {
        scanf("%d %d", &n, &m);
        n++, m++;
        for (int i = 0; i < n; i++) scanf("%lld", A + i);
        for (int i = 0; i < m; i++) scanf("%lld", B + i);
        for (int k = 0; k < n+m-1; k++)
            for (int i = 0; i <= k; i++)
                C[k] += A[i] * B[k - i];
        for (int i = 0; i< n + m - 1; i++) 
            printf("%lld ", C[i]);
        return 0;
    }

模板题亲测 44 分。

---

算法理论

上面的主要部分还是写了一个\(O(N^2)\)的暴力，那我们要寻找一个更快的办法：

就是它！\(FFT\)算法

前面我们已经说过：\(FFT\)算法是一个\(O(NlogN)\)的算法，但常数较大(相信你们会卡常)，并且，\(FFT\)是\(DFT\)和\(IDFT\)的快速算法：

---

思想：

首先你要会点值表达式，当然我们已经讲过。

然后我们来看\(A(x)=x^2+3x-2\)（红色）与\(B(x)=-x^2+6x+4\)(绿色)的取点得到点的点值表达式:

在\(A(x)\)上取三个点（紫色）\((-4,2)(-2,-4)(1,2)\)；在\(B(x)\)上取三个点\((0,4)(2,12)(6,4)\)，然后转为系数表达\(O(N^2)\)相乘然后再带入\(x\)得到\(C\)的点值表达式？这时绝对不行的，我们上面说过，点值表达式相乘可以在\(O(n)\)内解决，那怎么办呢？

我们可以取\(3\)个\(x\)相同的点：

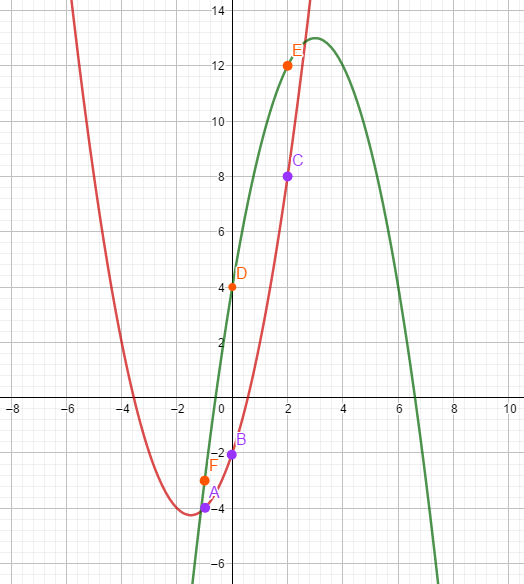
这样就行了？那是不可能的。我们知道，两个二次项式相乘得到的是一个四次项式，而\(C(x)=y_1*y_2\)，只能得到三个点，这肯定是不行的。

这很明显我们需要\(2n+1\)个点，不够怎么办呢？再添两个不就好了？
下面添加了\(I,J\)(横坐标相同)，\(G,H\)(横坐标相同)，这样就行了。

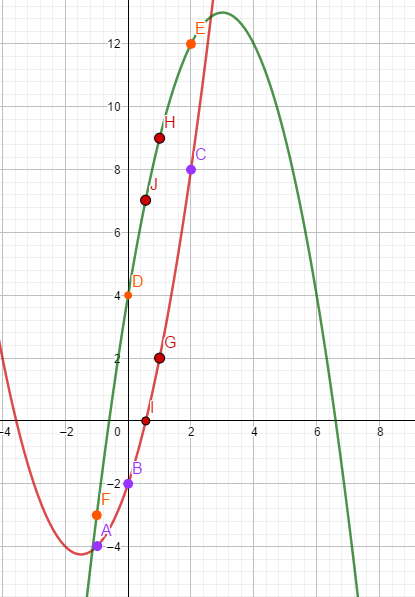
那么，我们只需要进行\(2n+1\)次乘法即可，省略常数（都说了常数巨大了），复杂度\(O(N)\)

神仙问题：\(tql\) \(but\) 这有用吗

当然有用啊：

算法流程：

\[ \text{系数表达式}\implies \text{点值表达式} \implies \text{系数表达式}\]

这不就有个用了吗？

但这个思路仅仅是\(DFT+IDFT\)，而\(FFT\)是用来加速\(DFT\)和\(IDFT\)的。

如果让我们求点值表达式，那我们肯定会带整数进去，因为这样好计算。但是傅里叶，（不知道是不是脑抽了），把复数带进了多项式中，然后神奇的事情就发生了……

我们把多项式如下拆开：

\(F(x)=(a_0+a_2x^2+…+a_{n-2}x^{n-2})+(a_1x^1+a_3x^3+…+a_{n-1}x^{n-1})\)

（保证\(n=2^k,k∈N^*\))

然后设两个有\(n/2\)次项的多项式\(FL(x)\)和\(FR(x)\)

\[FL(x)=a_0+a_2x+…+a_{n-2}x^{\frac{n}{2}-1}\]

\[FR(x)=a_1+a_3x+…+a_{n-1}x^{\frac{n}{2}-1}\]

\[F(x)=FL(x^2)+xFR(x^2)\]

设\(k<\frac{n}{2}\)，把\(ω_n^k\)代入\(F(x)\)：\(F(ω_n^k)=FL(ω_n^{2k})+ω_n^kFR(ω_n^{2k})\)

接着，就有\(F(ω_n^k)=FL(ω_{n/2}^{k})+ω_n^kFR(ω_{n/2}^{k})\)

那么，如果我们知道\(FL(x),FR(x)\)分别在\(ω^0_{n/2},ω^1_{n/2},…,ω^{n/2-1}_{n/2}\)处的点值表示，那么我们就可以\(O(N)\)内求出\(F(x)\)在\(ω^0_{n},ω^1_{n},…,ω^{n/2-1}_{n}\)处的点值表示了。

接下来我们的目标就是求\(F(x)\)在\(ω^{n/2}_{n},ω^{n/2+1}_{n},…,ω^{n-1}_{n}\)处的点值表示。

然后……

继续设\(k<n/2\)，然后把\(ω^{k+n/2}_{n}\)代入\(F(x)\)中。

运用一系列单位根的性质，读者可以自行证明出：

\[F(ω^{k+n/2}_{n})=FL(ω^{k}_{n/2})-ω^{k}_{n}FR(ω^{k}_{n/2})\]

然后我们就可以求出\(F(x)\)在\(ω^0_{n},ω^1_{n},…,ω^{n-1}_{n}\)处的点值表示，接着，我们就实现了\(DFT\)（听着好累的样子……）

但是我们还不知道\(FL(x),FR(x)\)在\(ω^0_{n},ω^1_{n},…,ω^{n/2-1}_{n}\)处的点值表示。难道要暴力代入吗？这样反而会使时间复杂度上升。

但是我们想想：\(FL(x)\)和\(FR(x)\)是由原来问题\(F(x)\)转化来的，怎么转化的？看到这里，你应该想到了分治。我们知道，分治的时间复杂度是\(logN\)，好像完成了一半了？

然后，因为\(FL(x),FR(x)\)是\(F(x)\)的子问题，那么我们可以对它们继续进行分解成一个个小的子问题，然后再合并，类似于归并排序。

\(FFT\)分治的合并过程根据：

1. \(F(ω^{k}_{n})=FL(ω^{k}_{n/2})+ω^{k}_{n}FR(ω^{k}_{n/2})\)

2. \(F(ω^{k+n/2}_{n})=FL(ω^{k}_{n/2})-ω^{k}_{n}FR(ω^{k}_{n/2})\)

从理论到实现

上文的所有证明都基于\(2=2^k,k∈N^*\)，但是我们做题的时候并没有这一点，所以我们可以补一些系数为\(0\)的项，这对计算结果没有影响。

---

1. 预处理单位根

我们知道一个性质\(ω_n^k=(ω_n^1)^k\)

那么，我们只要知道\(ω_n^1\)就可以求出\(ω_n^0,ω_n^1,ω_n^2,…,ω_n^{n-1}\)。

怎么求\(ω_n^1\)？

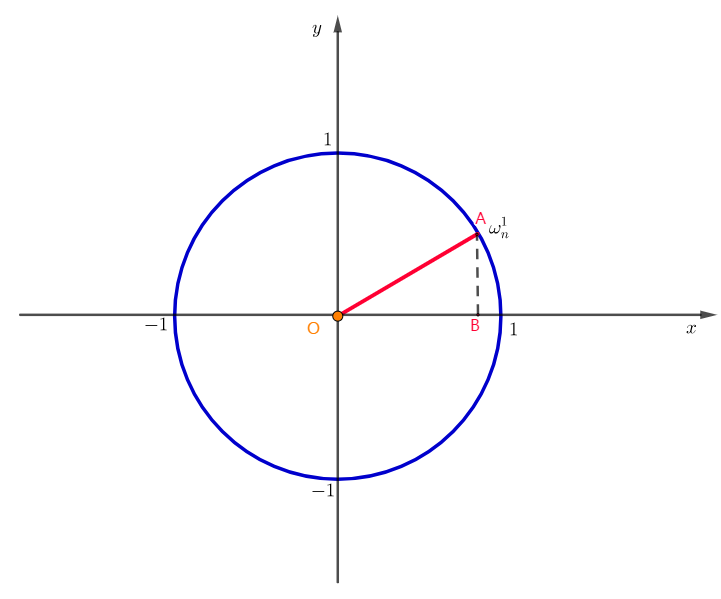
解三角形不就好了？已知\(|OA|=1\),幅角是\(\frac{1}{n}\)圆周，那么：

(由于\(c++\)下三角函数用弧度制表示，以下全部使用弧度制。)

设幅角\(α=\frac{2π}{n}\),，则\(ω_n^1(cos\big(\frac{2π}{n} \big),sin\big(\frac{2π}{n} \big))\)。

这边要牢记，\(x\)是实轴，\(y\)是虚轴：

    struct complex { //复数 
        long double a, b;
        complex() { a = b = 0;}
            //重载复数四则运算 
        complex operator + (const complex x) const {
            complex temp;
            temp.a = a + x.a;
            temp.b = b + x.b;
            return temp; 
        }

        complex  operator - (const complex x) const {
            complex temp;
            temp.a = a - x.a;
            temp.b = b - x.b;
            return temp; 
        }

        complex operator * (const complex x) const {
            complex temp;
            temp.a = a * x.a - b * x.b;
            temp.b = a * x.b + b * x.a;
            return temp; 
        }

        complex operator *= (const complex &x) {
            *this = *this * x;
            return *this;
        }

        complex operator / (const complex x) const {
            double div = x.a * x.a + x.b * x.b;
            complex temp;
            temp.a = (a * x.a + b * x.b) / div;
            temp.b = (b * x.a - a * x.b) / div;
            return temp; 
        }
    }w[SIZE],temp, buf;

    void unit_roots(int n) {
        const long double pi = 3.14159265358979;
        //complex ;
        temp.a = cos(2*pi/n), temp.b = sin(2*pi/n);
        w[0].a = 1, w[0].b = 0;
        buf.a = 1, buf.b = 0;
        for(int i = 1; i < n ; i++) {
            buf *= temp;
            w[i] = buf; 
        }
        for(int i = 0; i < n; i++)
            printf("w_%d %.3Lf %.3Lf\n", i, w[i].a, w[i].b);    
    } 

然后我们就可以实现\(DFT\)了

因为还没讲\(IDFT\)，先写\(DFT\):

递归\(DFT\)实现（复数板子上面有了下面就不写了）

    int n, m;
    Complex f[SIZE];
    void dft(Complex *f, int len) { //当前子问题长度
        if(len == 0) return;
        Complex fl[len + 10], fr[len + 10];
        for(int i = 0 ; i < len; i++)
            fl[i] = f[i << 1], fr[i] = f[i << 1 | 1];
        dft(fl, len >> 1);
        dft(fr, len >> 1);
        len *= 2;
        Complex temp, buf;
        temp.a = cos(2*pi/n), temp.b = sin(2*pi/n);
        buf.a = 1;
        for(int i = 0 ; i < len / 2; i++) {
            f[i] = fl[i] + buf * fr[i];
            f[i + len / 2] = fl[i] - buf * fr[i];
            buf *= temp;
        }
    }
    int main() {

        scanf("%d", &n);
        for(int i = 0; i < n; i++) scanf("%Lf", &f[i].a);
        for(m = 1; m < n; m <<= 1);//补到2的幂次方
        dft(f, m >> 1);
        for(int i = 0; i < m; i++) printf("%.3Lf ", f[i].a);
        return 0;
    }

事实上虚数可以用(小心TLE)：

            complex <double> f;

然后我们得到了一堆点值表达……

这并没有什么用

于是，我们现在来学习\(IDFT\)——\(DFT\)的逆运算。

刚刚的多项式为\(F(x)\)，系数是\(A\)数列，点值表示成\(M\)，\(M[k]=\sum \limits_{i=0}^{n-1}(ω_n^{k})^i*F[i]\)

然后就有\(F[k]=\frac{1}{n}\sum \limits_{i=0}^{n-1}(ω_n^{-k})^i*M[i]\)

结论记住就好了，可以自己尝试证明。

我们可以先求出和式，然后再除以\(n\)。

接下来我们求出\(ω_n^0,ω_n^{-1},…ω_n^{-n+1}\)

并且仍有：\(ω_n^{-j}=(ω_n^{-1})^j\)

所以我们还是求出\(ω_0^{-1}\)即可，并且，\(ω_0^{-1}\)与\(ω_0^{1}\)关于\(y\)轴对称。

    #include<iostream>
    #include<cstdio>
    #include<cmath>
    using namespace std;
    const long double pi = 3.141592653589793;
    const int SIZE = 4e6 + 10;
    struct complex { //复数 
        long double real, imag;
        complex() { real = imag = (double)0;}
            //重载复数四则运算 
        complex operator + (const complex x) const {
            complex temp;
            temp.real = real + x.real;
            temp.imag = imag + x.imag;
            return temp; 
        }

        complex  operator - (const complex x) const {
            complex temp;
            temp.real = real - x.real;
            temp.imag = imag - x.imag;
            return temp; 
        }

        complex operator * (const complex x) const {
            complex temp;
            temp.real = real * x.real - imag * x.imag;
            temp.imag = real * x.imag + imag * x.real;
            return temp; 
        }

        complex operator *= (const complex &x) {
            *this = *this * x;
            return *this;
        }

        complex operator / (const complex x) const {
            double div = x.real * x.real + x.imag * x.imag;
            complex temp;
            temp.real = (real * x.real + imag * x.imag) / div;
            temp.imag = (imag * x.real - real * x.imag) / div;
            return temp; 
        } 
        void conj() { imag = -imag; } 
    }a[SIZE], b[SIZE];

    complex omega(int n, int k) {
        complex temp;
        temp.real = cos(2 * pi * k / n);
        temp.imag = sin(2 * pi * k / n);
        return temp;
    }   
    int n, m, p;        
    void fft(complex *f, int len, int inv) {
        if(len == 1) return;
        int mid = len >>1;
        complex fl[mid + 10], fr[mid + 10];
        for(int i = 0; i < mid; i++)
            fl[i] = f[i << 1], fr[i] = f[i << 1 | 1];
        fft(fl, mid, inv);
        fft(fr, mid, inv);
        complex temp, buf; 
        temp.real = cos(2 * pi / len);
         temp.imag = sin(2 * pi / len);
        buf.real = 1, buf.imag = 0;
        if(inv) temp.conj();
        for(int i = 0; i < mid; i++, buf *= temp) {
            complex s = buf * fr[i];
            f[i] = fl[i] + s;
            f[i + mid] = fl[i] - s;
        }
    }

    int main() {

        scanf("%d %d", &n, &m);
        for(p = 1; p < n + m + 1; p <<= 1);
        for(int i = 0; i <= n; i++) 
            scanf("%Lf", &a[i].real);
        for(int i = 0; i <= m; i++) 
            scanf("%Lf", &b[i].real);
        fft(a, p, 0);
        fft(b, p, 0);
        for(int i = 0; i < p; i++) 
            a[i] *= b[i];
        fft(a, p, 1);
        for(int i = 0; i <= n + m; i++)
            printf("%d ", (int)(a[i].real / p + 0.5));
    return 0;
}

接着TLE了……(丝毫没有卡常的欲望)

因为递归常数巨大，并且很容易爆空间。(但实际上是因为写了\(long \ double\)炸了)

下面是AC的递归代码，以后不要写long double 了

    #include<iostream>
    #include<cstdio>
    #include<cmath>
    using namespace std;
    const double pi = 3.141592653589793;
    const int SIZE = 4e6 + 10;
    struct complex { //复数 
        double real, imag;
        complex() { real = imag = (double)0;}
            //重载复数四则运算 
        complex operator + (const complex x) const {
            complex temp;
            temp.real = real + x.real;
            temp.imag = imag + x.imag;
            return temp; 
        }

        complex  operator - (const complex x) const {
            complex temp;
            temp.real = real - x.real;
            temp.imag = imag - x.imag;
            return temp; 
        }

        complex operator * (const complex x) const {
            complex temp;
            temp.real = real * x.real - imag * x.imag;
            temp.imag = real * x.imag + imag * x.real;
            return temp; 
        }

        complex operator *= (const complex &x) {
            *this = *this * x;
            return *this;
        }

        complex operator / (const complex x) const {
            double div = x.real * x.real + x.imag * x.imag;
            complex temp;
            temp.real = (real * x.real + imag * x.imag) / div;
            temp.imag = (imag * x.real - real * x.imag) / div;
            return temp; 
        } 

        void conj() { imag = -imag;}
    }a[SIZE], b[SIZE];

    complex omega(int n, int k) {
        complex temp;
        temp.real = cos(2 * pi * k / n);
        temp.imag = sin(2 * pi * k / n);
        return temp;
    }   
    int n, m, p;        
    void fft(complex *f, int len, int inv) {
        if(len == 1) return;
        int mid = len >>1;
        complex fl[mid + 10], fr[mid + 10];
        for(int i = 0; i < mid; i++)
            fl[i] = f[i << 1], fr[i] = f[i << 1 | 1];
        fft(fl, mid, inv);
        fft(fr, mid, inv);
        complex temp, buf; 
        temp.real = cos(2 * pi / len);
         temp.imag = sin(2 * pi / len);
        buf.real = 1, buf.imag = 0;
        if(inv) temp.conj();
        for(int i = 0; i < mid; i++, buf *= temp) {
            complex s = buf * fr[i];
            f[i] = fl[i] + s;
            f[i + mid] = fl[i] - s;
        }
    }

    int main() {

        scanf("%d %d", &n, &m);
        for(p = 1; p < n + m + 1; p <<= 1);
        for(int i = 0; i <= n; i++) 
            scanf("%lf", &a[i].real);
        for(int i = 0; i <= m; i++) 
            scanf("%lf", &b[i].real);
        fft(a, p, 0);
        fft(b, p, 0);
        for(int i = 0; i < p; i++) 
            a[i] *= b[i];
        fft(a, p, 1);
        for(int i = 0; i <= n + m; i++)
            printf("%d ", (int)(a[i].real / p + 0.5));
        return 0;
    }

实际上跑的很快的递归评测记录。

那有没有更优化的办法呢？这是肯定的。

---

蝴蝶变换

先看一张图

这张图是什么？这不是我们分治的顺序吗？

我在一开始和结束都打上了二进制，你有没有什么发现？

是的，每一个数的二进制都反过来了。

然后我们的任务就转换成求二进制反序：

    rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << l)//l是二进制位数
    //rev[i]是i翻转得到的

结论牢记即可。

还记得\(DP\)吗？（貌似没什么关系）

我们用循环实现\(FFT\)，也就像\(DP\)一样定义状态、阶段决策：

• 第一层循环枚举变换区间大小（阶段），第二层循环枚举开头（决策），第三层处理区间。

    #include<iostream>
    #include<cstdio>
    #include<cmath>
    using namespace std;
    const double pi = 3.141592653589793;
    const int SIZE = 4e6 + 10;
    struct complex { //复数 
        double real, imag;
        complex() { real = imag = (double)0;}
            //重载复数四则运算 
        complex operator + (const complex x) const {
            complex temp;
            temp.real = real + x.real;
            temp.imag = imag + x.imag;
            return temp; 
        }

        complex operator += (const complex &x) {
            *this = *this + x;
            return *this;
        }

        complex  operator - (const complex x) const {
            complex temp;
            temp.real = real - x.real;
            temp.imag = imag - x.imag;
            return temp; 
        }

        complex operator * (const complex x) const {
            complex temp;
            temp.real = real * x.real - imag * x.imag;
            temp.imag = real * x.imag + imag * x.real;
            return temp; 
        }

        complex operator *= (const complex &x) {
            *this = *this * x;
            return *this;
        }

        complex operator / (const complex x) const {
            double div = x.real * x.real + x.imag * x.imag;
            complex temp;
            temp.real = (real * x.real + imag * x.imag) / div;
            temp.imag = (imag * x.real - real * x.imag) / div;
            return temp; 
        } 
    }a[SIZE], b[SIZE];
    int n, m, p, L = -1;
    int rev[SIZE];

    void fft(complex *f, int inv) {
        for(int i = 0 ; i < p ; i++) 
            if(i < rev[i]) 
                swap(f[i], f[rev[i]]);
        for(int len = 2; len <= p; len <<= 1) {
            int length = len >> 1;
            complex temp;
            temp.real = cos(pi / length);
            temp.imag = sin(pi / length);
            if(inv) temp.imag = -temp.imag;
            for(int l = 0; l < p; l += len) {
                complex buf; buf.real = 1;
                for(int k = l; k < l + length; k++) {
                    complex t = buf * f[k + length];
                    f[k + length] = f[k] - t;
                    f[k] += t;
                    buf *= temp;
                }
            }
        }
    }

    int main() {
        scanf("%d %d", &n, &m);
        for(int i = 0; i <= n; i++)
            scanf("%lf", &a[i].real);
        for(int i = 0; i <= m; i++)
            scanf("%lf", &b[i].real);
        for(p = 1; p < n + m + 1; p <<= 1, L++);
        //l是位数，因为会多算一位，一开始初值直接给-1
        for(int i = 1; i < p; i++)
            rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << L);
        fft(a, 0), fft(b, 0);
        for(int i = 0; i < p; i++)
            a[i] *= b[i];
        fft(a, 1);
        for(int i = 0; i <= n + m; i++)
            printf("%d ", (int)(a[i].real / p + 0.5));
        return 0;
    } 

评测记录

NTT——快速数论变换

• 首先，学习\(NTT\)算法你要学会\(FFT\)（理解也可）（刚刚我们才讲完你不会忘了吧……）（我认为我写的很详细了呢\(QAQ\)）。

• 接下来，你要确保你会原根这个东西（起码要知道），不过我在后面还会再提，具体可以先看我的这一篇博客：同余相关，在比较下面的部分（由于还待完善，所以只是写了一点）。

• 然后就是希望大家看了这一篇博客对\(NTT\)有所了解，可能我讲的不好，但是起码你要知道\(NTT\)是什么。

---

前置知识

（怎么又是前置知识）

\(FFT\)

上面已经说了先理解\(FFT\)，并且我也给了写的比较详细的博客，这里不再展开。

但其实\(FFT\)并不是重点，而是里面用于优化的很重要的一个东西：\(\color{red}{\text{单位根}}\)。

---

• 原根

但是如果 \(FFT\) 要求取模呢？

\[\color{red}{What?\text{你不会？}}\]

好像因为 \(FFT\) 用的单位根不太好取模（复数），所以我们可能需要找一个东西来替代下单位根，那么就要求这个东西和单位根具有类似的性质。然后科学家们就开始寻找了……（也不知道是谁找到的）接下来他们找到了原根。

---

首先我们要了解一下啥是原根。（如果你看了上面给出的博客你应该知道了）

原根的定义

其实在那一篇博客里的原根定义很容易让人摸不着头脑……为啥呢？

\[\color{green}{δ_m(a)=φ(m) \text{？} what \ is \ this?}\]

因为它很不好求……那我们不妨换一种说法：

设 \(p\) 为质数，则根据 \(\color{orange}{\text{费马小定理}}\)，有：

\[\text{对于任意 }p\nmid a,a^{p-1}\equiv1 \pmod{p}\]

\[\color{red}{\text{那么称 $g$ 为模 $p$ 的原根，当且仅当}\{g^0,g^1,…,g^{p-2}\}\text{对} \ p \ \text{的模数互不相同。}}\]

这样可能会更好理解些？至于为什么是上面那个绿绿的，我也不知道啊……

• 补充：本原单位根

其实定义很简单，对于一些比较特殊的\(n\)次单位根，它的\(0,1,…,n-1\)次幂恰好生成了所有的\(n\)次单位根，我们把这样的单位根称为本原单位根。

在复数域 \(C\) 上，\(\omega_n=\exp\frac{2\pi i}{n}=\cos\frac{2\pi}{n}+i\sin\frac{2\pi}{n}\) 是一个本原单位根。

（以上不是重点，下面这句话才是重点）

在有限域（即模质数）上，本原单位根和数论中的原根有关！

这也是我补充本原单位根的原因了……因为后面我们还会提到它。

并且我们可以证明的是，模质数的原根总是存在的（不知道为啥你就问度娘吧）。

并且原根的性质和单位根非常相似哦~

\(NTT\) 里原根的性质

换句话说，在模 \(p\) 意义下，\(g\) 可以被看做一个 \(p-1\) 次本原单位根。

反正感性理解就好，结论不就是用来记的嘛……

设 \(n\mid p-1\) ,我们不妨令 \(\omega_n=g^{\frac{p-1}{n}}\)（这个其实很像单位根的求法），然后你就可以得到一大串东西了：（好像也不多）

\[\omega_n^n=(g^{\frac{p-1}{n}})^n=g^{p-1}\equiv1\pmod p\]

并且因为单位根的定义，你会知道 \(\omega_n^0,\omega_n^0,…,\omega_n^{n-1}\) 互不相同……这不就完了嘛 $QAQ $

因此此时的 \(\omega_n\) 在模 \(p\) 意义下具有 \(n\) 次本原单位根的性质，所以我们利用这个东西来定义 \(DFT\) 即可，这被称为 \(\color{red}{NTT}\)。

原根的求法

求模质数原根的办法： 将 \(p-1\) 分解质因数，即 \(p-1=p_1^{a_1}p_2^{a2}…p_{n}^{a_n}\) 为标准的\(p-1\)分解式，那么若 \(g^{\frac{p-1}{p_i}}\ne 1\pmod p\) ，则\(g\)是模 \(p\) 意义下的一个原根。

求模合数原根的办法： 其实你只需要把上面的 \(p-1\) 换成 \(φ(p)\) 即可。

证明：（假设法）
  先对于第一种模质数的情况：
  假设存在一个 \(t<φ(p)=p-1\) 使得 \(g^t\equiv1\pmod p\) 且 \(\forall i∈[1,n],g^{\frac{p-1}{p_i}}\ne 1 \pmod p\)。由裴蜀定理可知：一定存在一组 \((a,b)\) 使得：\(a*t=(p-1)*b+gcd(t,p-1)\) 成立。由欧拉定理/费马小定理：\(g^{p-1}\equiv 1 \pmod p\)。所以 \(g^{a*t}\equiv g^{(p-1)*b+gcd(t,p-1)}\equiv1\pmod p\)。因为 \(t<p-1\)，所以又有 \(gcd(t,p-1)<p-1\)。又因为 \(gcd(t,p-1)\mid p-1\)，于是 \(\exists i ∈[1,n],gcd(t,p-1)\mid{g^{\frac{p-1}{p_i}}}\)。那么就可以得到 \(g^{\frac{p-1}{p_i}}\equiv g^{gcd(t, p-1)}\equiv 1 \pmod p\)。
 因此假设不成立。所以原命题成立。
\(Q.E.D.\)

那么上述结论自然可以推广到模合数而把 \(p-1\) 改为 \(φ(p)\) 了。

以上的证明是针对于这一句话的：\(δ_m(a)=φ(m)\)，也就是上述求法成立的条件。我们从另一个性质出发，即 \(g^0,g^1,…,g^{p-1}\) 模\(p\)的余数各不相同，那么可以得知这些余数的集合为：\(\{1,2,…p-1\}\)（不分顺序）。我们知道取模是满足乘法性质的。也就是说，如果\(\exists i∈[1,n]\)使得\(g^{\frac{p-1}{p^i}}=1\)，我们知道唯有 \(g^0 \bmod p=1 \bmod p = 1\) ，那么很明显 \(\frac{p-1}{p^i}\) 是不会为 \(0\) 的，那么一旦出现第一个数字的重复，也就是 \(1\)，那么很明显不满足原根的上述性质。

那么我就很好奇，为什么重复的\(1\)一定会出现在某个\(g^{\frac{p-1}{p^i}}\)当中呢？上面其实也已经证明，如果存在某个 \(t<φ(p)\) 使得 \(g^t\equiv1\pmod p\) 成立，那么必定会存在一个 \(g^\frac{p-1}{p^i}\bmod p=1\) 。并且我认为这样可能更好理解。

反正证明这种东西感性理解一下就好了……

然后原根你也会求了，所以用原根 \(g\) 去代替 \(FFT\) 中的 \(\omega_n\) (即单位根),就可以完成 \(FFT\) 了。

NTT 模数

首先根据 \(FFT\) 我们知道 \(g^{\frac{p-1}{n}}\)中的 \(n\) 是 \(2\) 的幂次，所以在做 \(FFT\) 的时候我们最好构造形如 \(p=a*2^k+1\)的质数，这样就可以满足上面的需求了。这样的质数最好取大一点（精度），所以这样的质数可以取：

\(p=a*2^k+1\)	\(\\) \(a\)	\(k\)	\(g\)
\(3\)	\(1\)	\(1\)	\(2\)
\(5\)	\(1\)	\(2\)	\(2\)
\(17\)	\(1\)	\(4\)	\(3\)
\(97\)	\(3\)	\(5\)	\(5\)
\(193\)	\(3\)	\(6\)	\(5\)
\(257\)	\(1\)	\(8\)	\(3\)
\(7681\)	\(15\)	\(9\)	\(17\)
\(12289\)	\(3\)	\(12\)	\(11\)
\(40961\)	\(5\)	\(13\)	\(3\)
\(65537\)	\(1\)	\(16\)	\(3\)
\(786433\)	\(3\)	\(18\)	\(10\)
\(5767169\)	\(11\)	\(19\)	\(3\)
\(7340033\)	\(7\)	\(20\)	\(3\)
\(23068673\)	\(11\)	\(21\)	\(3\)
\(104857601\)	\(25\)	\(22\)	\(3\)
\(167772161\)	\(5\)	\(25\)	\(3\)
\(469762049\)	\(7\)	\(26\)	\(3\)
\(\color{red}{998244353}\)	\(119\)	\(23\)	\(3\)
\(\color{red}{1004535809}\)	\(479\)	\(21\)	\(3\)
\(1998585857\)	\(953\)	\(21\)	\(3\)
\(2013265921\)	\(15\)	\(27\)	\(31\)
\(2281701377\)	\(17\)	\(27\)	\(3\)
\(3221225473\)	\(3\)	\(30\)	\(5\)
\(75161927681\)	\(35\)	\(31\)	\(3\)
\(77309411329\)	\(9\)	\(33\)	\(7\)
\(206158430209\)	\(3\)	\(36\)	\(22\)
\(2061584302081\)	\(15\)	\(37\)	\(7\)
\(2748779069441\)	\(5\)	\(39\)	\(3\)
\(6597069766657\)	\(3\)	\(41\)	\(5\)
\(39582418599937\)	\(9\)	\(42\)	\(5\)
\(79164837199873\)	\(9\)	\(43\)	\(5\)
\(263882790666241\)	\(15\)	\(44\)	\(7\)
\(1231453023109121\)	\(35\)	\(45\)	\(3\)
\(1337006139375617\)	\(19\)	\(46\)	\(3\)
\(3799912185593857\)	\(27\)	\(47\)	\(5\)
\(4222124650659841\)	\(15\)	\(48\)	\(10\)
\(7881299347898369\)	\(7\)	\(50\)	\(6\)
\(31525197391593473\)	\(7\)	\(52\)	\(3\)
\(180143985094819841\)	\(5\)	\(55\)	\(6\)
\(1945555039024054273\)	\(27\)	\(56\)	\(5\)
\(4179340454199820289\)	\(29\)	\(57\)	\(3\)

理论到实现

第一件事，我们先来回忆一下 \(FFT\)，而 \(FFT\) 分为两个步骤：\(DFT\) 与 \(IDFT\)。

然后我们知道单位根的定义是对于复数域 \(C\)，有 \(z^n=1\) 的复数就是一个 \(n\)次单位根，\(n\) 次单位根有 \(n\) 个，为：\(e^{\frac{2\pi k}{n}i}, \ k = \{0,1,2…,n-1\}\)（\(i\)是虚数单位）。（你用三角表示也是可以的，但是不好理解）

然后这里就用 \(g^{\frac{p-1}{n}}\) 代替 上面那个就可以，因为你会发现他们具有相同的性质。

唯一具有卷积性质的变换就是 \(DFT\)，按照上面的式子，\(DFT\) 的变换式就是：

\[X_k=\sum_{n=0}^{N-1}x_ne^{-\frac{2\pi}{N}nki} \ \ \ \ \ \ k=0,1,2…,N-1\]

\(DFT\) 反演（也就是逆变换）公式有：

\[x_n=\frac{1}{N}\sum_{k=0}^{N-1}X_ke^{\frac{2\pi}{N}nki} \ \ \ \ \ \ n=0,1,2…N-1\]

那么由于 \(g^{\frac{p-1}{n}}\) 和 \(e^{\frac{2\pi k}{n}i}, \ k = \{0,1,2…,n-1\}\) 等价，所以：

\[e^{-\frac{2\pi}{N}nki}\equiv g^{\frac{p-1}{N}}\pmod p\]

接着我们就得到了快速数论变换的公式：

\[X_k=\sum_{n=0}^{N-1}x_ng^{nk}\pmod p \ \ \ \ \ \ k=0,1,2…,N-1\]

反演：

\[x_n=\frac{1}{N}\sum_{k=0}^{N-1}X_kg^{-nk}\pmod p\ \ \ \ \ \ n=0,1,2…N-1\]

这样我们就成功把复数域转到了整数域，然后剩下的东西在\(\mod p\)意义下考虑即可。上面也已经讲过素数的构造方法。

• 补充：原根为何可以代替单位根？

考虑单位根的性质（也就是我们为什么使用单位根）：

1. \(n\) 个单位根互不相同。那么\(g^0,g^1,…,g^{p-2}\) 在模 \(p\) 意义下也不相同，成立。

2. \(z^n=1\)（\(z∈C\)）。根据费马小定理：\(g^{p-1}\equiv 1\pmod p\)，成立。

3. 单位根对称分布。其实这对于原根也成立。

证明：
  \(∵(g^{\frac{p-1}{2}})^2\equiv g^{p-1}\equiv 1 \pmod p\)
  又\(∵g^i \ne g^j(i\ne j \text{且}0≤i,j≤p-1)\)
  \(∴g^{\frac{p-1}{2}}= \ne 1,\text{则}g^{\frac{p-1}{2}}=-1\)
\(Q.E.D.\)

好了，我们真的可以使用 \(NTT\) 来完成 \(FFT\) 所能完成和所不能完成的事了。

可以尝试过一下模板题：\(P3803\)【模板】多项式乘法(\(FFT\))

虽然题目没有要求模数，但是仍然可以取一个比较大的模数从而完成。

这里取 \(p=998244353,g=3\)。

我们结合代码来理解 \(NTT\) :

#include<bits/stdc++.h>
using namespace std;
const int N = (1 << 21) + 100, P = 998244353, G = 3;

inline int read() {
    static int x, f;
    static char c;
    while(!isdigit(c = getchar()) && c != '-');
    x = (f = c == '-') ? 0 : c - '0';
    while(isdigit(c = getchar())) 
        x = (x << 3) + (x << 1) + (c ^ 48);
    return f ? -x + 1 : x;
}

typedef long long ll;
inline ll power(ll a, ll k) {
    ll base = 1;
    for(; k; k >>= 1) {
        if(k & 1) base = (base * a) % P;
        a = (a * a) % P;
    }   
    return base;
}

int rev[1 << 21], limit = 1;
ll a[N], b[N];
inline void NTT(ll *f, int inv) {
    for(int i = 0; i < limit; i++)
        if(i < rev[i]) swap(f[i], f[rev[i]]);
    
    for(int len = 1; len < limit; len <<= 1) {
        ll temp = power(G, (P - 1) / (len << 1));
        if(inv) temp = power(temp, P - 2);
        //反NTT时，除法全部变为乘逆元 
        for(int l = 0; l < limit; l += len * 2) {
            ll w = 1;
            for(int k = 0; k < len; k++) {
                int x = f[l + k], y = w * f[l + k + len] % P;
                f[l + k] = (x + y) % P;
                f[l + k + len] = (x - y + P) % P;
                w = (w * temp) % P;
            }
        }
    } 
}

int main() {
    int n = read(), m = read(), L = -1;
    for(int i = 0; i <= n; i++) a[i] = (read() + P) % P;
    for(int i = 0; i <= m; i++) b[i] = (read() + P) % P;
    for( ; limit <= n + m; limit <<= 1, L++); 
    for(int i = 0; i < limit; i++)
        rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << L);
    NTT(a, 0), NTT(b, 0);
    for(int i = 0; i < limit; i++)
        a[i] = (a[i] * b[i]) % P;
    NTT(a, 1);
    ll inv = power(limit, P - 2);
    for(int i = 0; i <= n + m; i++)
        printf("%lld ", (a[i] * inv) % P);
    
    return 0;
}

然后真的比\(FFT\)快好多呀……模板题评测记录：

\(\text{递归}FFT\)：点我

\(\text{蝴蝶变换}FFT\)：点我

\(NTT\)：点我