FCM算法
一.原理介绍
模糊C均值(Fuzzy C-means)算法简称FCM算法,是一种基于目标函数的模糊聚类算法,主要用于数据的聚类分析。理论成熟,应用广泛,是一种优秀的聚类算法。
首先介绍一下模糊这个概念,所谓模糊就是不确定,确定性的东西是什么那就是什么,而不确定性的东西就说很像什么。比如说把20岁作为年轻不年轻的标准,那么一个人21岁按照确定性的划分就属于不年轻,而我们印象中的观念是21岁也很年轻,这个时候可以模糊一下,认为21岁有0.9分像年轻,有0.1分像不年轻,这里0.9与0.1不是概率,而是一种相似的程度,把这种一个样本属于结果的这种相似的程度称为样本的隶属度,一般用u表示,表示一个样本相似于不同结果的一个程度指标。
基于此,假定数据集为X,如果把这些数据划分成c类的话,那么对应的就有c个类中心为C,每个样本j属于某一类i的隶属度为uijuij,那么定义一个FCM目标函数(1)及其约束条件(2)如下所示:
J=∑i=1c∑j=1numij||xj−ci||2(1)
(1)J=∑i=1c∑j=1nuijm||xj−ci||2
∑i=1cuij=1,j=1,2...,n(2)
(2)∑i=1cuij=1,j=1,2...,n
看一下目标函数(式1)而知,由相应样本的隶属度与该样本到各个类中心的距离相乘组成的,m是一个隶属度的因子,个人理解为属于样本的轻缓程度,就像x2x2与x3x3这种一样。式(2)为约束条件,也就是一个样本属于所有类的隶属度之和要为1。观察式(1)可以发现,其中的变量有uij、ciuij、ci,并且还有约束条件,那么如何求这个目标函数的极值呢?
这里首先采用拉格朗日乘数法将约束条件拿到目标函数中去,前面加上系数,并把式(2)的所有j展开,那么式(1)变成下列所示:
J=∑i=1c∑j=1numij||xj−ci||2+λ1(∑i=1cui1−1)+...+λj(∑i=1cuij−1)+...+λn(∑i=ncuin−1))(3)
(3)J=∑i=1c∑j=1nuijm||xj−ci||2+λ1(∑i=1cui1−1)+...+λj(∑i=1cuij−1)+...+λn(∑i=ncuin−1))
现在要求该式的目标函数极值,那么分别对其中的变量uij、ciuij、ci求导数,首先对uijuij求导。
分析式(3),先对第一部分的两级求和的uijuij求导,对求和形式下如果直接求导不熟悉,可以把求和展开如下:
⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢um11||x1−c1||2⋮umi1||x1−ci||2⋮umc1||x1−cc||2⋯⋮⋯⋮⋯um1j||xj−c1||2⋮umij||xj−ci||2⋮umcj||xj−cc||2⋯⋮⋯⋮⋯um1n||xn−c1||2⋮umin||xn−ci||2⋮umcn||xn−cc||2⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥
[u11m||x1−c1||2⋯u1jm||xj−c1||2⋯u1nm||xn−c1||2⋮⋮⋮⋮⋮ui1m||x1−ci||2⋯uijm||xj−ci||2⋯uinm||xn−ci||2⋮⋮⋮⋮⋮uc1m||x1−cc||2⋯ucjm||xj−cc||2⋯ucnm||xn−cc||2]
这个矩阵要对uijuij求导,可以看到只有uijuij对应的umij||xj−ci||2uijm||xj−ci||2保留,其他的所有项中因为不含有uijuij,所以求导都为0。那么umij||xj−ci||2uijm||xj−ci||2对uijuij求导后就为m||xj−ci||2um−1ijm||xj−ci||2uijm−1。
再来看后面那个对uijuij求导,同样把求和展开,再去除和uijuij不相关的(求导为0),那么只剩下这一项:λj(uij−1)λj(uij−1),它对uijuij求导就是λjλj了。
那么最终J对uijuij的求导结果并让其等于0就是:
∂J∂uij=m||xj−ci||2um−1ij+λj=0
∂J∂uij=m||xj−ci||2uijm−1+λj=0
这个式子化简下,将uijuij解出来就是:
um−1ij=−λjm||xj−ci||2
uijm−1=−λjm||xj−ci||2
进一步:
uij=(−λjm||xj−ci||2)1m−1=(−λjm)1m−1(1||xj−ci||(2m−1))(4)(4)uij=(−λjm||xj−ci||2)1m−1=(−λjm)1m−1(1||xj−ci||(2m−1))
要解出uijuij则需要把λjλj去掉才行。这里重新使用公式(2)的约束条件,并把算出来的uijuij代入式(2)中有:
1=∑i=1cuij=∑i=1c(−λjm)1m−1(1||xj−ci||(2m−1))=(−λjm)1m−1∑i=1c(1||xj−ci||(2m−1))1=∑i=1cuij=∑i=1c(−λjm)1m−1(1||xj−ci||(2m−1))=(−λjm)1m−1∑i=1c(1||xj−ci||(2m−1))
这样就有(其中把符号i换成k):
(−λjm)1m−1=(1∑i=1c(1||xj−ci||(2m−1)))=(1∑k=1c(1||xj−ck||(2m−1)))(−λjm)1m−1=(1∑i=1c(1||xj−ci||(2m−1)))=(1∑k=1c(1||xj−ck||(2m−1)))
把这个重新代入到式(4)中有:
uij=(1∑k=1c(1||xj−ck||(2m−1)))(1||xj−ci||(2m−1))=(1∑k=1c(||xj−ci||(2m−1))||xj−ck||(2m−1)))=1∑k=1c(||xj−ci||||xj−ck||)(2m−1)(5)(5)uij=(1∑k=1c(1||xj−ck||(2m−1)))(1||xj−ci||(2m−1))=(1∑k=1c(||xj−ci||(2m−1))||xj−ck||(2m−1)))=1∑k=1c(||xj−ci||||xj−ck||)(2m−1)
好了,式子(5)就是最终的uijuij迭代公式。
下面在来求J对cici的导数。由公式(2)可以看到只有∑i=1c∑j=1numij||xj−ci||2∑i=1c∑j=1nuijm||xj−ci||2这一部分里面含有cici,对其二级求和展开如前面所示的,那么它对cici的导数就是:
∂J∂ci=∑j=1n(−umij∗2∗(xj−ci))=0∂J∂ci=∑j=1n(−uijm∗2∗(xj−ci))=0
即:
∑j=1n(umijci)=∑j=1n(xjumij)∑j=1n(uijmci)=∑j=1n(xjuijm) ci=∑j=1n(xjumij)∑j=1numij(6)(6)ci=∑j=1n(xjuijm)∑j=1nuijm
好了,公式(6)就是类中心的迭代公式。
我们发现uijuij与cici是相互关联的,彼此包含对方,有一个问题就是在fcm算法开始的时候既没有uijuij也没有cici,那要怎么求解呢?很简单,程序开始的时候我们随便赋值给uijuij或者cici其中的一个,只要数值满足条件即可。然后就开始迭代,比如一般的都赋值给uijuij,那么有了uijuij就可以计算cici,然后有了cici又可以计算uijuij,反反复复,在这个过程中还有一个目标函数J一直在变化,逐渐趋向稳定值。那么当J不在变化的时候就认为算法收敛到一个比较好的结了。可以看到uijuij和cici在目标函数J下似乎构成了一个正反馈一样,这一点很像EM算法,先E在M,有了M在E,在M直至达到最优。
公式(5),(6)是算法的关键。现在来重新从宏观的角度来整体看看这两个公式,先看(5),在写一遍
uij=1∑k=1c(||xj−ci||||xj−ck||)(2m−1)
uij=1∑k=1c(||xj−ci||||xj−ck||)(2m−1)
假设看样本集中的样本1到各个类中心的隶属度,那么此时j=1,i从1到c类,此时上述式中分母里面求和中,分子就是这个点相对于某一类的类中心距离,而分母是这个点相对于所有类的类中心的距离求和,那么它们两相除表示什么,是不是表示这个点到某个类中心在这个点到所有类中心的距离和的比重。当求和里面的分子越小,是不是说就越接近于这个类,那么整体这个分数就越大,也就是对应的uijuij就越大,表示越属于这个类,形象的图如下:
再来宏观看看公式(6),考虑当类i确定后,式(6)的分母求和其实是一个常数,那么式(6)可以写成:
ci=∑j=1n(xjumij)∑j=1numij=∑j=1numij∑j=1numijxj
ci=∑j=1n(xjuijm)∑j=1nuijm=∑j=1nuijm∑j=1nuijmxj
这是类中心的更新法则。说这之前,首先让我们想想kmeans的类中心是怎么更新的,一般最简单的就是找到属于某一类的所有样本点,然后这一类的类中心就是这些样本点的平均值。那么FCM类中心怎么样了?看式子可以发现也是一个加权平均,类i确定后,首先将所有点到该类的隶属度u求和,然后对每个点,隶属度除以这个和就是所占的比重,乘以xjxj就是这个点对于这个类i的贡献值了。
(二)简单程序实现
下面我们在matlab下用最基础的循环实现上述的式(5)与式(6)的FCM过程。首先,我们需要产生可用于FCM的数据,为了可视化方便,我们产生一个二维数据便于在坐标轴上显示,也就是每个样本由两个特征(或者x坐标与y坐标构成),生成100个这样的点,当然我们在人为改变一下,让这些点看起来至少属于不同的类。生成的点画出来如下:
那么我们说FCM算法的一般步骤为:
(1)确定分类数,指数m的值,确定迭代次数(这是结束的条件,当然结束的条件可以有多种)。
(2)初始化一个隶属度U(注意条件—和为1);
(3)根据U计算聚类中心C;
(4)这个时候可以计算目标函数J了
(5)根据C返回去计算U,回到步骤3,一直循环直到结束。
还需要说一点的是,当程序结束后,怎么去判断哪个点属于哪个类呢?在结束后,肯定有最后一次计算的U吧,对于每一个点,它属于各个类都会有一个u,那么找到其中的最大的u就认为这个点就属于这一类。基于此一个基础的程序如下:
clc
clear
close all
%% create samples:
for i=1:100
x1(i) = rand()*5; %人为保证差异性
y1(i) = rand()*5;
x2(i) = rand()*5 + 3; %人为保证差异性
y2(i) = rand()*5 + 3;
end
x = [x1,x2];
y = [y1,y2];
data = [x;y];
data = data';%一般数据每一行代表一个样本
%plot(data(:,1),data(:,2),'*'); %画出来
%%---
cluster_n = 2;%类别数
iter = 50;%迭代次数
m = 2;%指数
num_data = size(data,1);%样本个数
num_d = size(data,2);%样本维度
%--初始化隶属度u,条件是每一列和为1
U = rand(cluster_n,num_data);
col_sum = sum(U);
U = U./col_sum(ones(cluster_n,1),:);
%% 循环--规定迭代次数作为结束条件
for i = 1:iter
%更新c
for j = 1:cluster_n
u_ij_m = U(j,:).^m;
sum_u_ij = sum(u_ij_m);
sum_1d = u_ij_m./sum_u_ij;
c(j,:) = u_ij_m*data./sum_u_ij;
end
%-计算目标函数J
temp1 = zeros(cluster_n,num_data);
for j = 1:cluster_n
for k = 1:num_data
temp1(j,k) = U(j,k)^m*(norm(data(k,:)-c(j,:)))^2;
end
end
J(i) = sum(sum(temp1));
%更新U
for j = 1:cluster_n
for k = 1:num_data
sum1 = 0;
for j1 = 1:cluster_n
temp = (norm(data(k,:)-c(j,:))/norm(data(k,:)-c(j1,:))).^(2/(m-1));
sum1 = sum1 + temp;
end
U(j,k) = 1./sum1;
end
end
end
figure;
subplot(1,2,1),plot(J);
[~,label] = max(U); %找到所属的类
subplot(1,2,2);
gscatter(data(:,1),data(:,2),label)
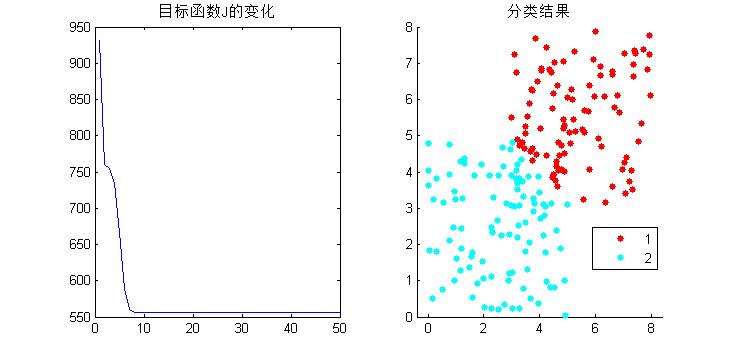
得到结果如下:
基于此,结果还算正确。但是不得不说的一个问题就是算法的效率问题。为了和公式计算方式吻合,便于理解,这个程序里面有很多的循环操作,当分类数大一点,样本多一点的时候,这么写是很慢的,matlab号称矩阵实验室,所以要尽量少的使用循环,直接矩阵操作,那么上述的操作很多地方是可以把循环改成矩阵计算的,这里来介绍下matlab自带的fcm函数,就是使用矩阵运算来的。
Matlab下help fcm既可以查阅相关用法们这里只是简单介绍,fcm函数输入需要2个或者3个参数,返回3个参数,如下:
[center, U, obj_fcn] = fcm(data, cluster_n, options)
对于输入:data数据集(注意每一行代表一个样本,列是样本个数)
cluster_n为聚类数。
options是可选参数,完整的options包括:
OPTIONS(1): U的指数 (default: 2.0)
OPTIONS(2): 最大迭代次数 (default: 100)
OPTIONS(3): 目标函数的最小误差 (default: 1e-5)
OPTIONS(4): 是否显示结果 (default: 1,显示)
options都有默认值,自带的fcm结束的条件是OPTIONS(2)与OPTIONS(3)有一个满足就结束。
对于输出:center聚类中心,U隶属度,obj_fcn目标函数值,这个迭代过程的每一代的J都在这里面存着。
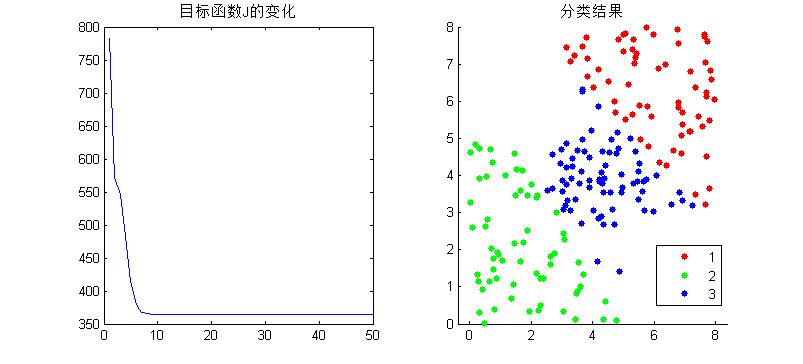
为了验证我们写的算法是否正确,用它的fcm去试试我们的数据(前提是数据一样),分成3类,画出它们的obj_fcn看看如下:
可以看到,虽然迭代的中间过程不一样,但是结果却是一样的。
K-means算法
一.原理介绍
K-means算法是最为经典的基于划分的聚类方法,是十大经典数据挖掘算法之一。K-means算法的基本思想是:以空间中k个点为中心进行聚类,对最靠近他们的对象归类。通过迭代的方法,逐次更新各聚类中心的值,直至得到最好的聚类结果。
k-means 算法接受参数 k ,然后将事先输入的n个数据对象划分为 k个聚类以便使得所获得的聚类满足,同一聚类中的对象相似度较高,而不同聚类中的对象相似度较小。聚类相似度是利用各聚类中对象的均值所获得一个“中心对象”(引力中心)来进行计算的。
实现原理
KMeans算法的基本思想是初始随机给定K个簇中心,按照最邻近原则把待分类样本点分到各个簇。然后按平均法重新计算各个簇的质心,从而确定新的簇心。一直迭代,直到簇心的移动距离小于某个给定的值。
K-Means聚类算法主要分为三个步骤:
(1)第一步是为待聚类的点寻找聚类中心;
(2)第二步是计算每个点到聚类中心的距离,将每个点聚类到离该点最近的聚类中去;
(3)第三步是计算每个聚类中所有点的坐标平均值,并将这个平均值作为新的聚类中心;
反复执行(2)、(3),直到聚类中心不再进行大范围移动或者聚类次数达到要求为止。
下图展示了对n个样本点进行K-means聚类的效果,这里k取2:
(a)未聚类的初始点集;
(b)随机选取两个点作为聚类中心;
(c)计算每个点到聚类中心的距离,并聚类到离该点最近的聚类中去;
(d)计算每个聚类中所有点的坐标平均值,并将这个平均值作为新的聚类中心;
(e)重复(c),计算每个点到聚类中心的距离,并聚类到离该点最近的聚类中去;
(f)重复(d),计算每个聚类中所有点的坐标平均值,并将这个平均值作为新的聚类中心。
该算法的最大优势在于简洁和快速。算法的关键在于初始中心的选择和距离公式。
数据描述:Iris数据集包含150个牡丹花模式样本,其中 每个模式样本采用5维的特征描述
X = (x1,x2,x3,x4,w);
x1: 萼片长度(厘米)
x2: 萼片宽度(厘米)
x3: 花瓣长度(厘米)
x4:花瓣宽度(厘米)
w(类别属性 ): 红牡丹(Iris setosa),白牡丹(Iris versicolor)和黄牡丹(Iris virginica)
% 函数功能 : 实现对iris.data数据集的分类,并根据分类结果进行精度评价
clear;clc;close all;
%手动选取文件,选用iris.data
[filename,fpath] = uigetfile(...
{...
'*.m;*.txt;*.data',...
'Data(*.m;*.txt;*.data)';...
'*.*','All Files(*.*)'...
},'Select data');
if ~filename
return
end
% filename = 'iris.data';
[X1,X2,X3,X4,X5] = textread(filename,'%f%f%f%f%s','delimiter',','); %Get data
clear filename fpath
X = [X1 X2 X3 X4];
[m,~] = size(X);
%分配索引
DataLabel = zeros(m,1);
DataLabel(strcmp(X5,'Iris-setosa')) = 1;
DataLabel(strcmp(X5,'Iris-versicolor')) = 2;
DataLabel(strcmp(X5,'Iris-virginica')) = 3;
clear m X5
%二维结果
[MyCenter1,ClusterLabel12] = FindCluster([X1 X2],3,DataLabel);
[MyCenter2,ClusterLabel13] = FindCluster([X1 X3],3,DataLabel);
[MyCenter3,ClusterLabel14] = FindCluster([X1 X4],3,DataLabel);
[MyCenter4,ClusterLabel23] = FindCluster([X2 X3],3,DataLabel);
[MyCenter5,ClusterLabel24] = FindCluster([X2 X4],3,DataLabel);
[MyCenter6,ClusterLabel34] = FindCluster([X3 X4],3,DataLabel);
hold on;
subplot(231)
MyPlot2(X1,X2,DataLabel,MyCenter1),xlabel('X1'),ylabel('X2')
subplot(232)
MyPlot2(X1,X3,DataLabel,MyCenter2),xlabel('X1'),ylabel('X3')
subplot(233)
MyPlot2(X1,X4,DataLabel,MyCenter3),xlabel('X1'),ylabel('X4')
subplot(234)
MyPlot2(X2,X3,DataLabel,MyCenter4),xlabel('X2'),ylabel('X3')
subplot(235)
MyPlot2(X2,X4,DataLabel,MyCenter5),xlabel('X2'),ylabel('X4')
subplot(236)
MyPlot2(X3,X4,DataLabel,MyCenter6),xlabel('X3'),ylabel('X4')
clear MyCenter1 MyCenter2 MyCenter3 MyCenter4 MyCenter5 MyCenter6
%三维结果
[MyCenter7,ClusterLabel123] = FindCluster([X1,X2,X3],3,DataLabel);
[MyCenter8,ClusterLabel124] = FindCluster([X1,X2,X4],3,DataLabel);
[MyCenter9,ClusterLabel134] = FindCluster([X1,X3,X4],3,DataLabel);
[MyCenter10,ClusterLabel234] = FindCluster([X2,X3,X4],3,DataLabel);
hold on;
figure,title('3D');
subplot(221)
MyPlot3(X1,X2,X3,DataLabel,MyCenter7)
xlabel('X1'),ylabel('X2'),zlabel('X3');
subplot(222)
MyPlot3(X1,X2,X4,DataLabel,MyCenter8)
xlabel('X1'),ylabel('X2'),zlabel('X4');
subplot(223)
MyPlot3(X1,X3,X4,DataLabel,MyCenter9)
xlabel('X1'),ylabel('X3'),zlabel('X4');
subplot(224)
MyPlot3(X2,X3,X4,DataLabel,MyCenter10)
xlabel('X2'),ylabel('X3'),zlabel('X4');
clear MyCenter7 MyCenter8 MyCenter9 MyCenter10
%聚类精度评价
%二维结果
ClusterLabel_2D = [ClusterLabel12,ClusterLabel13,ClusterLabel14...
ClusterLabel23,ClusterLabel24,ClusterLabel34];
ClusterAccuracy_2D = Accuracy(DataLabel,ClusterLabel_2D);
clear ClusterLabel12 ClusterLabel13 ClusterLabel14
clear ClusterLabel23 ClusterLabel24 ClusterLabel34 ClusterLabel_2D
%三维结果
ClusterLabel_3D = [ClusterLabel123,ClusterLabel124,ClusterLabel134,ClusterLabel234];
ClusterAccuracy_3D = Accuracy(DataLabel,ClusterLabel_3D);
clear ClusterLabel123 ClusterLabel124 ClusterLabel134 ClusterLabel234
clear ClusterLabel_3D
FindCluster.m
%函数功能 : 输入数据集、聚类中心个数与样本标签
% 得到聚类中心与聚类样本标签
function [ClusterCenter,ClusterLabel] = FindCluster(MyData,ClusterCounts,DataLabel)
[m,n] = size(MyData);
ClusterLabel = zeros(m,1); %用于存储聚类标签
% MyLabel = unique(DataLabel,'rows');
% for i = 1:size(MyLabel,2);
% LabelIndex(1,i) = i; %为数据标签创建索引
% end
%已知数据集的每个样本的中心
OriginCenter = zeros(ClusterCounts,n);
for q = 1:ClusterCounts
DataCounts = 0;
for p = 1:m
%按照数据标签,计算样本中心
if DataLabel(p) == q
OriginCenter(q,:) = OriginCenter(q,:) + MyData(p,:);
DataCounts = DataCounts + 1;
end
end
OriginCenter(q,:) = OriginCenter(q,:) ./ DataCounts;
end
%按照第一列对样本中心排序
%排序是为了解决新聚类中心因随机分配而与样本最初的聚类中心不匹配的问题
SortCenter1 = sortrows(OriginCenter,1);
FalseTimes = 0;
CalcuateTimes = 0;
%此循环用于纠正分类错误的情况
while (CalcuateTimes < 15)
ClusterCenter = zeros(ClusterCounts,n); %初始化聚类中心
for p = 1:ClusterCounts
ClusterCenter(p,:) = MyData( randi(m,1),:); %随机选取一个点作为中心
end
%此循环用于寻找聚类中心
%目前还未解决该循环陷入死循环的问题,所以设置一个参数来终止循环
kk = 0;
while (kk < 15)
Distance = zeros(1,ClusterCounts); %存储单个样本到每个聚类中心的距离
DataCounts = zeros(1,ClusterCounts); %记录每个聚类的样本数目
NewCenter = zeros(ClusterCounts,n);
for p = 1:m
for q = 1:ClusterCounts
Distance(q) = norm(MyData(p,:) - ClusterCenter(q,:));
end
%index返回最小距离的索引,亦即聚类中心的标号
[~,index] = min(Distance);
ClusterLabel(p) = index;
end
k = 0;
for q = 1:ClusterCounts
for p = 1:m
%按照标记,对样本进行分类,并计算聚类中心
if ClusterLabel(p) == q
NewCenter(q,:) = NewCenter(q,:) + MyData(p,:);
DataCounts(q) = DataCounts(q) + 1;
end
end
NewCenter(q,:) = NewCenter(q,:) ./ DataCounts(q);
%若新的聚类中心与上一个聚类中心相同,则认为算法收敛
if norm(NewCenter(q,:) - ClusterCenter(q,:)) < 0.1
k = k + 1;
end
end
ClusterCenter = NewCenter;
%判断是否全部收敛
if k == ClusterCounts
break;
end
kk = kk + 1 ;
end
%再次判断每个聚类是否分类正确,若分类错误则进行惩罚
trueCounts = ClusterCounts;
SortCenter2 = sortrows(ClusterCenter,1);
for p = 1:ClusterCounts
if norm(SortCenter1(p,:) - SortCenter2(p,:)) > 0.5
trueCounts = trueCounts - 1;
FalseTimes = FalseTimes + 1;
break;
end
end
if trueCounts == ClusterCounts
break;
end
CalcuateTimes = CalcuateTimes + 1;
end
% FalseTimes
% CalcuateTimes
% trueCounts
% kk
% DataCounts
% OriginCenter
% NewCenter
%理论上每个聚类的标签应是123排列的,但实际上,由于每个聚类中心都是随机选取的,
%实际分类的顺序可能是213,132等,所以需要对分类标签进行纠正,这对之后的精度评
%价带来了方便。
%对分类标签进行纠正:
%算法原理:从第一个已知的样本中心开始,寻找离其最近的聚类中心,然后将归类于该
% 聚类中心的样本的聚类标签更换为i
for i = 1:ClusterCounts %遍历原始样本中心
for j = 1:ClusterCounts %遍历聚类中心,与原样本中心比较
if norm(OriginCenter(i,:) - ClusterCenter(j,:)) < 0.6
% for p = 1:m
% if ClusterLabel(p) == j
% ClusterLabel(p) = 2 * ClusterCounts + i;
% end
% end
ClusterLabel(ClusterLabel == j) = 2 * ClusterCounts + i;
end
end
end
ClusterLabel = ClusterLabel - 2 * ClusterCounts;
%Temp = [MyData(:,:),ClusterLabel]
%函数功能 : 输入样本,样本标签及求出的聚类中心,显示二维图像,实现数据可视化
function MyPlot2(X1,X2,DataLabel,ClusterCenter)
[m,~] = size(X1);
hold on;
% for p = 1:m
% if(DataLabel(p) == 1)
% plot(X1(p),X2(p),'*r')
% elseif(DataLabel(p) == 2)
% plot(X1(p),X2(p),'*g')
% else
% plot(X1(p),X2(p),'*b')
% end
% end
p = find(DataLabel == 1);
plot(X1(p),X2(p),'*r')
p = find(DataLabel == 2);
plot(X1(p),X2(p),'*g')
p = find(DataLabel == 3);
plot(X1(p),X2(p),'*b')
% xlabel(who('X1'));
% ylabel(who('X2'));
%PS : 我想在坐标轴中根据输入的形参的矩阵的名字,转换成字符串,来动态输出
% 坐标轴名称,不知道该怎么做?用上面注释的语句不行。。
[n,~] = size(ClusterCenter);
plot(ClusterCenter(1:1:n,1),ClusterCenter(1:1:n,2),'ok')
grid on;
MyPlot3.m
function MyPlot3(X1,X2,X3,DataLabel,ClusterCenter)
[m,~] = size(X1);
hold on;
% for i = 1:m
% if(DataLabel(i) == 1)
% plot3(X1(i),X2(i),X3(i),'.r')
% elseif(DataLabel(i) == 2)
% plot3(X1(i),X2(i),X3(i),'.g')
% else
% plot3(X1(i),X2(i),X3(i),'.b')
% end
% end
p = find(DataLabel == 1);
plot3(X1(p),X2(p),X3(p),'.r')
p = find(DataLabel == 2);
plot3(X1(p),X2(p),X3(p),'.g')
p = find(DataLabel == 3);
plot3(X1(p),X2(p),X3(p),'.b')
% xlabel('X1');
% ylabel('X2');
% zlabel('X3');
%PS : 我想在坐标轴中根据输入的形参的矩阵的名字,转换成字符串,来动态输出
% 坐标轴名称,不知道该怎么做?用上面注释的语句不行。。
[n,~] = size(ClusterCenter);
% for i = 1:n
% plot3(ClusterCenter(i,1),ClusterCenter(i,2),ClusterCenter(i,3),'ok')
% end
plot3(ClusterCenter(1:1:n,1),ClusterCenter(1:1:n,2),ClusterCenter(1:1:n,3),'ok')
view([1 1 1]);
grid on;
运行结果:
数据集:
5.1,3.5,1.4,0.2,Iris-setosa
4.9,3.0,1.4,0.2,Iris-setosa
4.7,3.2,1.3,0.2,Iris-setosa
4.6,3.1,1.5,0.2,Iris-setosa
5.0,3.6,1.4,0.2,Iris-setosa
5.4,3.9,1.7,0.4,Iris-setosa
4.6,3.4,1.4,0.3,Iris-setosa
5.0,3.4,1.5,0.2,Iris-setosa
4.4,2.9,1.4,0.2,Iris-setosa
4.9,3.1,1.5,0.1,Iris-setosa
5.4,3.7,1.5,0.2,Iris-setosa
4.8,3.4,1.6,0.2,Iris-setosa
4.8,3.0,1.4,0.1,Iris-setosa
4.3,3.0,1.1,0.1,Iris-setosa
5.8,4.0,1.2,0.2,Iris-setosa
5.7,4.4,1.5,0.4,Iris-setosa
5.4,3.9,1.3,0.4,Iris-setosa
5.1,3.5,1.4,0.3,Iris-setosa
5.7,3.8,1.7,0.3,Iris-setosa
5.1,3.8,1.5,0.3,Iris-setosa
5.4,3.4,1.7,0.2,Iris-setosa
5.1,3.7,1.5,0.4,Iris-setosa
4.6,3.6,1.0,0.2,Iris-setosa
5.1,3.3,1.7,0.5,Iris-setosa
4.8,3.4,1.9,0.2,Iris-setosa
5.0,3.0,1.6,0.2,Iris-setosa
5.0,3.4,1.6,0.4,Iris-setosa
5.2,3.5,1.5,0.2,Iris-setosa
5.2,3.4,1.4,0.2,Iris-setosa
4.7,3.2,1.6,0.2,Iris-setosa
4.8,3.1,1.6,0.2,Iris-setosa
5.4,3.4,1.5,0.4,Iris-setosa
5.2,4.1,1.5,0.1,Iris-setosa
5.5,4.2,1.4,0.2,Iris-setosa
4.9,3.1,1.5,0.1,Iris-setosa
5.0,3.2,1.2,0.2,Iris-setosa
5.5,3.5,1.3,0.2,Iris-setosa
4.9,3.1,1.5,0.1,Iris-setosa
4.4,3.0,1.3,0.2,Iris-setosa
5.1,3.4,1.5,0.2,Iris-setosa
5.0,3.5,1.3,0.3,Iris-setosa
4.5,2.3,1.3,0.3,Iris-setosa
4.4,3.2,1.3,0.2,Iris-setosa
5.0,3.5,1.6,0.6,Iris-setosa
5.1,3.8,1.9,0.4,Iris-setosa
4.8,3.0,1.4,0.3,Iris-setosa
5.1,3.8,1.6,0.2,Iris-setosa
4.6,3.2,1.4,0.2,Iris-setosa
5.3,3.7,1.5,0.2,Iris-setosa
5.0,3.3,1.4,0.2,Iris-setosa
7.0,3.2,4.7,1.4,Iris-versicolor
6.4,3.2,4.5,1.5,Iris-versicolor
6.9,3.1,4.9,1.5,Iris-versicolor
5.5,2.3,4.0,1.3,Iris-versicolor
6.5,2.8,4.6,1.5,Iris-versicolor
5.7,2.8,4.5,1.3,Iris-versicolor
6.3,3.3,4.7,1.6,Iris-versicolor
4.9,2.4,3.3,1.0,Iris-versicolor
6.6,2.9,4.6,1.3,Iris-versicolor
5.2,2.7,3.9,1.4,Iris-versicolor
5.0,2.0,3.5,1.0,Iris-versicolor
5.9,3.0,4.2,1.5,Iris-versicolor
6.0,2.2,4.0,1.0,Iris-versicolor
6.1,2.9,4.7,1.4,Iris-versicolor
5.6,2.9,3.6,1.3,Iris-versicolor
6.7,3.1,4.4,1.4,Iris-versicolor
5.6,3.0,4.5,1.5,Iris-versicolor
5.8,2.7,4.1,1.0,Iris-versicolor
6.2,2.2,4.5,1.5,Iris-versicolor
5.6,2.5,3.9,1.1,Iris-versicolor
5.9,3.2,4.8,1.8,Iris-versicolor
6.1,2.8,4.0,1.3,Iris-versicolor
6.3,2.5,4.9,1.5,Iris-versicolor
6.1,2.8,4.7,1.2,Iris-versicolor
6.4,2.9,4.3,1.3,Iris-versicolor
6.6,3.0,4.4,1.4,Iris-versicolor
6.8,2.8,4.8,1.4,Iris-versicolor
6.7,3.0,5.0,1.7,Iris-versicolor
6.0,2.9,4.5,1.5,Iris-versicolor
5.7,2.6,3.5,1.0,Iris-versicolor
5.5,2.4,3.8,1.1,Iris-versicolor
5.5,2.4,3.7,1.0,Iris-versicolor
5.8,2.7,3.9,1.2,Iris-versicolor
6.0,2.7,5.1,1.6,Iris-versicolor
5.4,3.0,4.5,1.5,Iris-versicolor
6.0,3.4,4.5,1.6,Iris-versicolor
6.7,3.1,4.7,1.5,Iris-versicolor
6.3,2.3,4.4,1.3,Iris-versicolor
5.6,3.0,4.1,1.3,Iris-versicolor
5.5,2.5,4.0,1.3,Iris-versicolor
5.5,2.6,4.4,1.2,Iris-versicolor
6.1,3.0,4.6,1.4,Iris-versicolor
5.8,2.6,4.0,1.2,Iris-versicolor
5.0,2.3,3.3,1.0,Iris-versicolor
5.6,2.7,4.2,1.3,Iris-versicolor
5.7,3.0,4.2,1.2,Iris-versicolor
5.7,2.9,4.2,1.3,Iris-versicolor
6.2,2.9,4.3,1.3,Iris-versicolor
5.1,2.5,3.0,1.1,Iris-versicolor
5.7,2.8,4.1,1.3,Iris-versicolor
6.3,3.3,6.0,2.5,Iris-virginica
5.8,2.7,5.1,1.9,Iris-virginica
7.1,3.0,5.9,2.1,Iris-virginica
6.3,2.9,5.6,1.8,Iris-virginica
6.5,3.0,5.8,2.2,Iris-virginica
7.6,3.0,6.6,2.1,Iris-virginica
4.9,2.5,4.5,1.7,Iris-virginica
7.3,2.9,6.3,1.8,Iris-virginica
6.7,2.5,5.8,1.8,Iris-virginica
7.2,3.6,6.1,2.5,Iris-virginica
6.5,3.2,5.1,2.0,Iris-virginica
6.4,2.7,5.3,1.9,Iris-virginica
6.8,3.0,5.5,2.1,Iris-virginica
5.7,2.5,5.0,2.0,Iris-virginica
5.8,2.8,5.1,2.4,Iris-virginica
6.4,3.2,5.3,2.3,Iris-virginica
6.5,3.0,5.5,1.8,Iris-virginica
7.7,3.8,6.7,2.2,Iris-virginica
7.7,2.6,6.9,2.3,Iris-virginica
6.0,2.2,5.0,1.5,Iris-virginica
6.9,3.2,5.7,2.3,Iris-virginica
5.6,2.8,4.9,2.0,Iris-virginica
7.7,2.8,6.7,2.0,Iris-virginica
6.3,2.7,4.9,1.8,Iris-virginica
6.7,3.3,5.7,2.1,Iris-virginica
7.2,3.2,6.0,1.8,Iris-virginica
6.2,2.8,4.8,1.8,Iris-virginica
6.1,3.0,4.9,1.8,Iris-virginica
6.4,2.8,5.6,2.1,Iris-virginica
7.2,3.0,5.8,1.6,Iris-virginica
7.4,2.8,6.1,1.9,Iris-virginica
7.9,3.8,6.4,2.0,Iris-virginica
6.4,2.8,5.6,2.2,Iris-virginica
6.3,2.8,5.1,1.5,Iris-virginica
6.1,2.6,5.6,1.4,Iris-virginica
7.7,3.0,6.1,2.3,Iris-virginica
6.3,3.4,5.6,2.4,Iris-virginica
6.4,3.1,5.5,1.8,Iris-virginica
6.0,3.0,4.8,1.8,Iris-virginica
6.9,3.1,5.4,2.1,Iris-virginica
6.7,3.1,5.6,2.4,Iris-virginica
6.9,3.1,5.1,2.3,Iris-virginica
5.8,2.7,5.1,1.9,Iris-virginica
6.8,3.2,5.9,2.3,Iris-virginica
6.7,3.3,5.7,2.5,Iris-virginica
6.7,3.0,5.2,2.3,Iris-virginica
6.3,2.5,5.0,1.9,Iris-virginica
6.5,3.0,5.2,2.0,Iris-virginica
6.2,3.4,5.4,2.3,Iris-virginica
5.9,3.0,5.1,1.8,Iris-virginica三.优缺点
优点:原理简单,实现容易
缺点:
1.收敛太慢
2.算法复杂度高O(nkt)
3.不能发现非凸形状的簇,或大小差别很大的簇
4.需样本存在均值(限定数据种类)
6.需先确定k的个数
7.对噪声和离群点敏感
8.最重要是结果不一定是全局最优,只能保证局部最优。