一、约瑟夫环介绍
讲一个比较有意思的故事:约瑟夫是犹太军队的一个将军,在反抗罗马的起义中,他所率领的军队被击溃,只剩下残余的部队40余人,他们都是宁死不屈的人,所以不愿投降做叛徒。一群人表决说要死,所以用一种策略来先后杀死所有人。
于是约瑟夫建议:每次由其他两人一起杀死一个人,而被杀的人的先后顺序是由抽签决定的,约瑟夫有预谋地抽到了最后一签,在杀了除了他和剩余那个人之外的最后一人,他劝服了另外一个没死的人投降了罗马。
我们这个规则是这么定的:
在一间房间总共有n个人(下标0~n-1),只能有最后一个人活命。
按照如下规则去杀人:
- 所有人围成一圈
- 顺时针报数,每次报到q的人将被杀掉
- 被杀掉的人将从房间内被移走
- 然后从被杀掉的下一个人重新报数,继续报q,再清除
- 直到剩余一人
你要做的是:当你在这一群人之间时,你必须选择一个位置以使得你变成那剩余的最后一人,也就是活下来。
.
.
二、以2为特例讲解
接下来我们说个特例初步了解下这种问题的求解思路:
特例:2,当q = 2时候,是一个特例,能快速求解
特例还分两种
1. 思路:注意这里的前提是n = 2^k(也就是2的幂次个人,其他数另外讨论)
如果只有2个人,显然剩余的为1号
如果有4个人,第一轮除掉2,4,剩下1,3,3死,留下1
如果是8个人,先除去2,4,6,8,之后3,7,剩下1,5,除去5,又剩下1了
……
定义J(n)为n个人构成的约瑟夫环最后结果,则有j(2^k) = 1
J(n) = 2^k – 2^k-1 = 2^k-1 n=2^k
J(n) = 2^k-1 – 2^k-2 = 2^k-2 n=2^k-1
………
J(2^2) = 2^2 – 2^1 = 2^1 n=2^2
递推得到如上结果,起始我们仔细分析也就是每次除去一半的元素,然后剩余的一半继续重复之前的策略,再除去一半。(可想到递归)
结合:J(2) = 1 我知道两个数,从1开始,肯定是2先死,剩下1.
得到:j(2^k) = 1
2. but当n 不等于 2^k时候,比如9,11这种:
n 不等于 2^k时,就不存在这样的easy的规律了,重新分析:
假设n = 9,这时候如图下:

能看出来,我们干掉第一个人也就是2,之后就只剩下8个人了,又回到J(2^k)上了,
这时候我们需要的是找到当前的1号元素。
见图下:
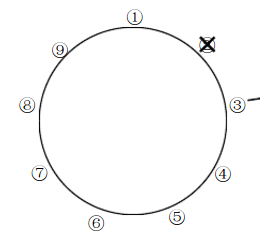
这时候,我们从3号开始,就成了另外一个规模小1的约瑟夫问题(恰好为2^k的特例)。
这时候,我们可以把3号看成新的约瑟夫问题中的1号位置:
J(8) = J(2^3) = 1,也就是说这里的1代表的就是上一个问题中的3号
So:J(9) = 3
答案为3号
同理可知所有的非2^k的数都是这样:
假设n = 2^k + t,t可以随意取,比如1,2,3…….
假设n = 11,这时候n = 2^ 3 + 3,也就是说t = 3,所以开始剔除元素直到其成为2^k问题的约瑟夫问题。
So,我们在剔除了t(3)个元素之后(分别是2,4,6),此时我们定格在2t+1(7)处,并且将2t+1(7)作为新的一号,而且这时候的约瑟夫环只剩下2^ 3,也就是J(2^3 + 3) = 2*3 + 1 = 7,答案为7
总结一下这个规律:
J(2^k + t) = 2t+1
.
.
三、一般情况
说完了特例,现在说说q 不等于2的情况下:
我们假定:
- n — n人构成的约瑟夫环
- q — 每次移除第q个人
约定:
- Jq(n)表示n人构成的约瑟夫环,每次移除第q个人的解
- n个人的编号从0开始至n-1
我们沿用之前特例的思想:能不能由Jq(n+1)的问题缩小成为J(n)的问题(这里的n是n+1规模的约瑟夫问题消除一个元素之后的答案),Jq(n)是在Jq(n+1)基础上移除一个人之后的解。也就是说,我们能由Jq(n)得到Jq(n+1)。
规律:Jq(n+1) = ( Jq(n) + q ) / (n+1)
大致是如下这样:
0 1 2 3 4 5 ...... n-1 总共n人
设第q个人也就是下标为q-1的那位,杀死:
剩下n-1个人,如下:
q q+1 q+2 ...... n-2 n-1 0 1 2 ...... q-2 (这里是除去q-1这位兄台的剩余n-1人)
这时,又来重复我们的老套路:将新的被杀的后一个人作为新的0号,于是新的如下:
0 1 2 ...... .......... ........ n-2
其实就是从q开始,到之前最大数n-1,每个数都减去q,
从0开始之后接着n-1这个新的值每次往后加1,直到加到n-2
举个例子:
J4(9) :
0 1 2 3 4 5 6 7 8 消去3--> 0 1 2 4 5 6 7 8( 0 1 2)
对应的新值: 0 1 2 3 4 5 6 7
其中:q=4,从3之后第一个数4开始:每个数5-q=1,6-q=2,7-q=3,8-q=4,因为是个环,0-q=-4,1-q=-3 ....直到加到n-1=7
这就相当于一个限定范围内的数的相对位置,-1代表的是最后一个元素,也就是之前的8
(-2就代表7,-3代表6,-4代表5.....-9代表0,从后面开始数过来第9位)
大致过程如图下:

那么我们知道是这么得到的新的队列,那么也很容易知道怎么反推了:
反观如上的变化情况,都是减去一个q,所以:
变回去的公式如下:old = (new + q) % n
这里的old和new指的是下标,n指的是总共有多少人
知道了怎么推出之前的下标,那么也就可以一步步递推回去得到开始的队列或者从小推到大得到最后剩余的结果。
.
.
四、代码示例
公式计算
Solution {
public:
int LastRemaining_Solution(unsigned int n, unsigned int m)
{
if(n==0)
return -1;
if(n==1)
return 0;
else
return (LastRemaining_Solution(n-1,m)+m)%n;
}
};
暴力破解
class Solution {
public:
int LastRemaining_Solution(int n, int m)
{
vector<int> array(n,0);
int i = -1, step = 0, count = n;
while (count > 0)
{
i++;
if (i >= n) i = 0;
if (array[i] == -1) continue;
step++;
if (step == m)
{
array[i] = -1;
step = 0;
count--;
}
}
return i;
}
};
暴力破解优化版
class Solution {
public:
int LastRemaining_Solution(int n, int m)
{
vector <int> array(n,0);
for (int i = 0; i < n; i++)
array[i] = i;
int pos = 0;
while (n > 1)
{
pos = (pos+m-1)%n;
array.erase(array.begin()+pos);
n--;
}
return n==1 ? array[0]:-1;
}
};