Manacher算法学习笔记

首先，强烈安利一篇文章，这篇文章对于\(Manacher\)的讲解本人感觉非常到位。

本文也是对上文的一个整理。~~虽然上文已经讲得很好了~~

一. 回文子串的一般解法

相信大家都知道的一个方法\(:\)枚举字符串的每一个位置作为回文子串的对称中心，同时向左向右扩展，判断是否相等，然后每次保存之前求取的最大回文子串长度，时间复杂度为\(O(n^2)\)。

在枚举时，还需要考虑对奇数回文串和偶数回文串分开处理，因为奇数回文串的对称中心是单个字符，而偶数回文串的对称中心为中间两字符的中间位置。为了结决这个问题，我们可以在每个字符的前后分别插入一个无关的字符\((\)具体是什么对结果无影响\()\)，这样无论是奇数串还是偶数串都会转变为奇数串。

二. \(Manacher\)算法

首先，介绍几个\(Manacher\)算法中的几个概念\(:\)

回文半径数组\(radius[i]\)，表示以\(i\)为对称中心的回文半径的长度，例如\(:\)

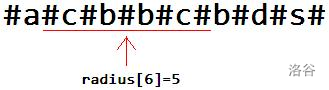
最右回文边界\(max\_r\)，表示当前位置及之前所有位置的回文子串所有到达的最右边的位置，例如\(:\)

最右回文边界的对称中心\(mid\)，即右边界为最右回文边界的回文子串的对称中心，例如\(:\)

然后，我们来说一下\(Manacher\)的算法流程\(:\)

第一种情况，当我们当前要扩展的点在最右回文边界\(max\_r\)的右侧时，由于其右侧点的情况我们还是未知的，所以我们只能采取朴素的做法，以要扩展的点为对称中心向两边扩展，同时更新\(radius\)数组，最右回文边界和最右回文边界的对称中心。

第二种情况，当我们要扩展的点在最右回文边界的左侧时，又要分三种情况来考虑\(:\)

首先说明一下下面将出现的变量\(:\) \(max\_l\)表示最右回文边界关于对称中心的对称点，\(p\)为当前要扩展的点，\(p_1\) 为当前要扩展的点关于对称中心的对称点，\(p_2\) 为以 \(p_1\) 为对称中心的回文子串的左边界。

\(1.\ \ p\leq max\_r\ \ and \ \ max\_l <p2\)

很显然，这种情况下，\(radius[p]=radius[p_1]\)。

\(2.\ \ p\leq max\_r\ \ and\ \ p_2 < max\_l\)

这种情况下，若我们仍取\(radius[p_1]\)，很显然就会涉及到\(max\_r\)之外我们未知的区域，所以\(radius[p]\)只能取\(max\_r-p\)。

\(3.\ \ p\leq max\_r\ \ and\ \ p_2==max\_l\)

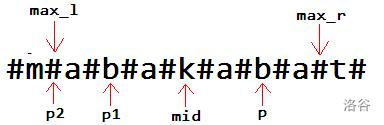
这种情况下，我们就需要继续向两边扩展\(p\)，但显然我们只需要从\(max\_r\)向右扩展即可。

那么，\(Manacher\)的算法流程大致就是这样了，下面我们来感性证明一下时间复杂度\(:\)

上面的两种情况中，第二种的\(1,2\)的时间复杂度都是\(O(1)\)的，第一种情况和第二种的\(3\)，\(max\_r\)都是不断向右扩展，没有回头的情况，在判断回文半径时也没有对\(max\_r\)内的点进行判断，所以\(max\_r\)是从字符串的左端点向右扩展到右端点，总复杂度为\(O(n)\)。

具体细节说清楚了，代码应该就很简单了。

code：

#include <iostream>
#include <cstdio>
#include <cstring>
#define min(a, b) ((a) < (b) ? (a) : (b))
#define max(a, b) ((a) > (b) ? (a) : (b))

using std::string;
const int maxn = 11000002;
string x, s;
int radius[maxn << 1], max_right, mid, ans;

int main() {
    std::cin >> x; s += '$', s += '#';
    for (int i = 0; i < x.length(); i++) s += x[i], s += '#';
    for (int i = 1; i < s.length(); i++) {
        radius[i] = max_right > i ? min(radius[mid * 2 - i], max_right - i) : 1;
        while (s[i - radius[i]] == s[i + radius[i]]) radius[i]++;
        if (i + radius[i] > max_right) max_right = i + radius[i], mid = i;
        ans = max(ans, radius[i] - 1);
    }
    printf("%d\n", ans);
    return 0;
}

完结撒花(✪ω✪)