班主任让数竞大佬jhc整理的三角函数复习题,我参与编辑完成。度盘pdf格式下载:复习题提取码fh6b,答案提取码5a12
“单纯”的运算
本文由蒋浩川原创,由\(MiserWeyte\)使用\(\LaTeX\)编辑,采用CC BY-SA 4.0协议发布。
一、公式
1、三角比
\(\sin\alpha=\dfrac{y}{r}\)
\(\cos\alpha=\dfrac{x}{r}\)
\(\tan\alpha=\dfrac{y}{x}\)
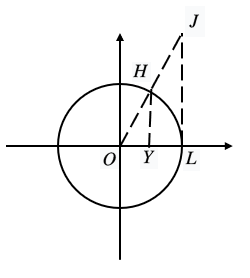
2、三角函数线
单位圆中:
\(\sin\alpha=|HY|\)
\(\sin\alpha=|OY|\)
\(\sin\alpha=|\ JL|\)
3.诱导公式xN
\(\sin(-\alpha)=-\sin\alpha\ \ \ \ \ \ \ \ \ \ \cos(-\alpha)=\cos\alpha\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \tan(-\alpha)=-\tan\alpha\)
\(\sin(\pi-\alpha)=\sin\alpha\ \ \ \ \ \ \ \ \ \cos(\pi-\alpha)=-\cos\alpha\ \ \ \ \ \ \ \ \ \tan(\pi-\alpha)=-\tan\alpha\)
\(\sin(\pi+\alpha)=-\sin\alpha\ \ \ \ \ \ \cos(\pi+\alpha)=-\cos\alpha\ \ \ \ \ \ \ \ \tan(\pi+\alpha)=\tan\alpha\)
\(\sin(\frac{\pi}{2}+\alpha)=\cos\alpha\ \ \ \ \ \ \ \ \cos(\frac{\pi}{2}+\alpha)=-\sin\alpha\ \ \ \ \ \ \ \ \tan(\frac{\pi}{2}+\alpha)=-\frac{1}{\tan\alpha}\)
\(\sin(\frac{\pi}{2}-\alpha)=\cos\alpha\ \ \ \ \ \ \ \ \cos(\frac{\pi}{2}-\alpha)=\sin\alpha\ \ \ \ \ \ \ \ \ \ \ \tan(\frac{\pi}{2}-\alpha)=\frac{1}{\tan\alpha}\)
4.和差倍半
\(\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta\)
\(\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta\)
\(\tan(\alpha+\beta)=\frac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta}\)
\(\sin(\alpha-\beta)=\sin\alpha\cos\beta-\cos\alpha\sin\beta\)
\(\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta\)
\(\tan(\alpha-\beta)=\frac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta}\)
\(\sin2\alpha=2\sin\alpha\cos\alpha\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \sin^2\frac{\alpha}{2}=\frac{1-\cos\alpha}{2}\)
\(\cos2\alpha=\cos^2\alpha-\sin^2\alpha\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \cos^2\frac{\alpha}{2}=\frac{1+\cos\alpha}{2}\)
\(\tan2\alpha=\frac{2\tan\alpha}{1-\tan^2\alpha}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \tan^2\frac{\alpha}{2}=\frac{1-\cos\alpha}{1+\cos\alpha}\)
5.辅助角公式
\(a\sin\alpha+b\cos\alpha=\sqrt{a^2+b^2}\sin(\alpha+\varphi)\)
\(\varphi=\arctan\frac{b}{a}\)
6.其他
\(1=\sin^2\alpha+\cos^2\alpha\)
\(2\cos^2\alpha=1+\cos2\alpha\)
\(2\sin^2\alpha=1-\cos2\alpha\)
二、练习
1.已知\(\angle\alpha\)终边上一点\(P(-3m,\ 4m)\),\(m\not=0\),求\(\alpha\)的三个三角比
2.设\(\alpha\in(2k\pi,\ 2k\pi+\frac{\pi}{2})(\pi\in Z)\),证明\(\sin\alpha<\alpha<\tan\alpha\)以及\(\sin\alpha+\cos\alpha>1\)
- 设:
\[f(x)=\begin{cases} \sin\pi x, \ x<0\\ f(x-1)+1, \ x\ge0 \end{cases}\ \ \ \ \ \ \ g(x)=\begin{cases} \cos\pi x, \ x<\frac{1}{2}\\ g(x-1)+1, \ x\ge\frac{1}{2} \end{cases} \]
求\(f(\frac{1}{3})+f(\frac{3}{4})+g(\frac{1}{4})+g(\frac{5}{6})\)
4.求\(\dfrac{\cos(2\pi-\alpha)\cdot\tan(-\alpha-\pi)\cdot\tan(3\pi-\alpha)}{\sin(\pi-\alpha)\cdot\tan(\pi-\alpha)}\ \ \ \ \ \ \ \ (\alpha\not=k\pi+\frac{\pi}{2})\)
5.设\(k\in Z\),求证\(\cos(k\pi+\alpha)=(-1)^k\cos\alpha\),\(\sin(k\pi+\alpha)=(-1)^k\sin\alpha\)。
6.求\(\alpha\):\((1)\sin\alpha=\frac{1}{2} \ \ \ \ \ \ \ (2)\tan\alpha=\frac{\sqrt{3}}{3}\)
7.已知\(\tan\alpha=2\)。求:
\((1)\dfrac{\sin\alpha+3\cos\alpha}{3\sin\alpha-4\cos\alpha}\ \ \ \ (2)\dfrac{\sin^2\alpha+8\sin\alpha\cos\alpha-6\cos^2\alpha}{3\sin^2\alpha-4\cos^2\alpha}\)
\((3)sin^2\alpha-3\sin\alpha\cos\alpha+4\cos^2\alpha-2\)
8.求\(\cos(\alpha+\frac{5}{12}\pi)\cos(\alpha+\frac{\pi}{6})+\cos(\frac{\pi}{12}-\alpha)\cos(\frac{\pi}{3}-\alpha)\)
9.已知\(\sin(\alpha+\frac{\pi}{6})=\frac{3}{5}\),\(\alpha\in(\frac{\pi}{3}, \frac{5}{6}\pi)\),求\(\tan(\alpha+\frac{5}{12})\)
10.若方程\(2\sin x+\sqrt5\cos x=\frac{1}{k}\)有解,求\(k\)范围。
11.求\(\sin10^\circ\cdot\sin50^\circ\cdot\sin70^\circ\)
12.\(\sin\alpha+\sin\beta=\)\(\frac{\sqrt2}{2}\),求\(\cos\alpha+\cos\beta\)范围。
三、拓展公式
\(\sin\alpha=\dfrac{2\tan\frac{\alpha}{2}}{1+\tan^2\frac{\alpha}{2}}\ \ \ \ \ \ \ \ \ \ \cos\alpha=\dfrac{1-\tan^2\frac{\alpha}{2}}{1+\tan^2\frac{\alpha}{2}}\ \ \ \ \ \ \ \ \ \ \tan\alpha=\dfrac{2\tan\frac{\alpha}{2}}{1-\tan^2\frac{\alpha}{2}}\)
和差化积与积化和差略。
\((\sin\alpha\pm\cos\alpha)^2=1\pm\sin2\alpha\)
\((1+\tan\alpha)(1+\tan\beta)=2\Longleftrightarrow\alpha+\beta=k\pi+\frac{\pi}{4},k\in Z\)
\(\sin(\alpha+\beta)\cdot\sin(\alpha-\beta)=\sin^2\alpha-\sin^2\beta=\cos^2\beta-\cos^2\alpha\)
\(\cos(\alpha+\beta)\cdot\cos(\alpha-\beta)=\cos^2\alpha-\sin^2\beta\)
四、综合与提升
1.
<指对幂与三角>
已知
\(\alpha\in(0, \frac{\pi}{4})\),
\(\beta\in(0, 1)\),试比较:
\(x=(\sin\alpha)^{\log_\beta\sin\alpha}\),
\(y=(\cos\alpha)^{\log_\beta\cos\alpha}\),
\(z=(\sin\alpha)^{\log_\beta\cos\alpha}\)
2. <提升> 设锐角 \(\theta\)使关于 \(x\)的方程 \(x^2+4x\cos\theta+\frac{1}{\tan\theta}=0\)有重根,求 \(\theta\)。
3. <提升> 求证 \(\dfrac{\cos\alpha}{1+\sin\alpha}-\dfrac{\sin\alpha}{1+\cos\alpha}=\dfrac{2(\cos\alpha-\sin\alpha)}{1+\cos\alpha+\sin\alpha}\)
4. <提升> 已知 \(\alpha\in(-\frac{\pi}{2},\frac{\pi}{2})\)且 \(\alpha\not=0\), \(\beta\in(0, \pi)\)且 \(\beta\not=\frac{\pi}{2}\), \(\sin\alpha=\sqrt2\cos\beta\), \(\tan\alpha\tan\beta=\sqrt3\),求 \(\alpha\), \(\beta\)
5. <提升> 已知 \(\dfrac{\sin^4\alpha}{\cos^2\beta}+\dfrac{\cos^4\alpha}{\sin^2\beta}=1\)且 \(\alpha,\beta\in(0,\dfrac{\pi}{2})\),求证 \(\alpha+\beta=\dfrac{\pi}{2}\)
6. <提升> 求 \(\cos\frac{2}{5}\pi+\cos\frac{4}{5}\pi\)
“单纯”的运算 参考答案
练习答案
- (1)当\(m>0\)时,\(\sin\alpha=\frac{4}{5}\),\(\cos\alpha=-\frac{3}{5}\),\(\sin\alpha=-\frac{4}{3}\)
(2)当\(m<0\)时,\(\sin\alpha=-\frac{4}{5}\),\(\cos\alpha=\frac{3}{5}\),\(\sin\alpha=-\frac{4}{3}\) - 如“三角函数线“图,\(\sin\alpha=|HY|,\alpha=\overset{\frown} {HL},\tan\alpha=|JL|\)
\(\therefore\sin\alpha<\alpha<\tan\alpha\)
\(\therefore\sin\alpha+\cos\alpha=|OY|+|HY|>|OH|=1\) - \(f(\frac{1}{3})=f(-\frac{2}{3})+1=-\frac{\sqrt3}{2}+1,\ \ f(\frac{3}{4})=f(-\frac{1}{4})+1=-\frac{\sqrt2}{2}+1\)
\(g(\frac{1}{4})=\frac{\sqrt2}{2},\ \ g(\frac{5}{6})=\frac{\sqrt3}{2}+1\)
\(\therefore\)所求\(=3\) - 原式\(=\dfrac{\cos\alpha\cdot(-\tan\alpha)\cdot(-\tan\alpha)}{\sin\alpha\cdot\tan\alpha}=1\)
- 蒋浩川说这题显而易见,略QwQ
- (1)\(\alpha=2k\pi+\frac{\pi}{6}\)或\(2k\pi+\frac{5}{6}\pi\ (k\in Z)\) (2)\(\alpha=k\pi+\frac{\pi}{6}\ (k\in Z)\)
- (1)原式\(=\frac{\tan\alpha+3}{3\tan\alpha-4}=\frac{5}{2}\)(2)原式\(=\frac{\tan^2\alpha+8\tan\alpha-6}{3\tan^2\alpha-4}=\frac{7}{4}\)
(3)原式\(=\frac{\tan^2\alpha-3\tan\alpha+2}{\tan^2\alpha+1}-2=-\frac{8}{5}\) - 原式\(=\cos(\alpha+\frac{\pi}{6})\sin(\frac{\pi}{12}-\alpha)+\cos(\frac{\pi}{12}-\alpha)\sin(\alpha+\frac{\pi}{6})=\sin\frac{\pi}{4}=\frac{\sqrt2}{2}\)
- \(\tan(\alpha+\frac{5}{12}\pi)=\dfrac{1+\tan(\alpha+\frac{\pi}{6})}{1-\tan(\alpha+\frac{\pi}{6})}\ \ \ \ \ \ \because\sin(\alpha+\frac{\pi}{6})=\frac{3}{5},\alpha+\frac{\pi}{6}\in(\frac{\pi}{2},\pi)\)
\(\therefore\tan(\alpha+\frac{\pi}{6})=-\frac{3}{4}\ \ \ \ \ \ \ \ \therefore\)所求\(=\frac{1}{7}\) - 左式\(=3\sin(\alpha+\theta),\theta=\arctan\frac{\sqrt5}{2}\ \ \ \ \ \ \ \\)\(\therefore\)左式\(\in[-3,3]\)
\(\therefore-3\leq\frac{1}{k}\leq3\ \ \ \ \ \ \ \ \ \ \ \ \therefore k\in[-\infty,-\frac{1}{3}]\cup[\frac{1}{3},\infty]\) - 所求\(=\cos80^\circ\cos40^\circ\cos20^\circ=\dfrac{\frac{1}{8}\sin160^\circ}{\sin20^\circ}=\dfrac{1}{8}\)
- \((\sin\alpha+\sin\beta)^2+(\cos\alpha+\cos\beta)^2=2+2\cos(x-y)\in[0,4]\)
\(\Rightarrow\cos\alpha+\cos\beta=\pm\sqrt{2+\cos(\alpha-y)-\frac{1}{2}}\in[-\frac{\sqrt{14}}{2},\frac{\sqrt{14}}{2}]\)
综合与提升答案
- \(\because f(x)=log_bx\)为减函数\(,b\in(0,1)\ \ \ \ \ \ \ \ 0\sin\alpha<\cos\alpha<1,\alpha\in(0,\frac{\pi}{4})\)
\(\Rightarrow\log_b\sin\alpha>\log_b\cos\alpha>0\)
\(\Rightarrow x<z,z<y \ \ \ \ \ \ \ \ \ \ \therefore x<z<y\) - 依题意\(\Delta=16\cos^2\theta-4\cot\theta=0\)且\(\cot\theta\not=0\)
\(\therefore\Delta=4\cot\theta(2\sin2\theta-1)=0\)
\(\Rightarrow\sin2\theta=\frac{1}{2}\Rightarrow\theta=\frac{\pi}{12}\)或\(\frac{5}{12}\pi\) - \(\dfrac{\cos\alpha}{1+\sin\alpha}=\dfrac{1-\sin\alpha}{\cos\alpha}=\dfrac{\cos\alpha+1-\sin\alpha}{1+\sin\alpha+\cos\alpha}\)
\(\dfrac{\sin\alpha}{1+\cos\alpha}=\dfrac{1-\cos\alpha}{\sin\alpha}=\dfrac{\sin\alpha+1-\cos\alpha}{1+\cos\alpha+\sin\alpha}\)
\(\Rightarrow\)所求证成立
- 两式平方并作商,\(\Rightarrow\cos^2\alpha=\frac{2}{3}\sin^2\beta\)
又\(\because\sin^2\alpha=2\cos^2\beta\)
两式相加\(\Rightarrow2\cos^2\beta+\frac{2}{3}\sin^2\beta=1\Rightarrow\sin^2\beta=\frac{3}{4}\)
\(\because\beta\in(0, \pi),\beta\not=\frac{\pi}{2}\ \ \ \ \ \ \ \ \therefore\sin\beta=\frac{\sqrt3}{2},\beta=\frac{\pi}{3}\)或\(\frac{2}{3}\pi\)
\[\therefore\begin{cases} \alpha=\frac{\pi}{4}\\ \beta=\frac{\pi}{3} \end{cases}\ \ \ 或 \begin{cases} \alpha=-\frac{\pi}{4}\\ \beta=\frac{2}{3}\pi \end{cases} \] - 令\(\dfrac{\sin^2\alpha}{\cos\beta}=\sin\theta\ \ \ \ \ \ \dfrac{\cos^2\alpha}{\sin\beta}=\cos\theta\ \ \ \ \ \ \theta\in(0, \dfrac{\pi}{2})\)
\(\therefore\sin\theta\cos\beta+\sin\beta\cos\theta=\sin^2\alpha+\cos^2\alpha=1\)
\(\Rightarrow\sin(\theta+\beta)=1\Rightarrow\sin\theta=\cos\beta\ \ \ \ \therefore\dfrac{\sin^2\alpha}{\cos\beta}=\sin\theta=\cos\beta\)
\(\therefore\sin\alpha=\cos\beta\ \ \ \ \ \ \ \ \ \ \ \ Q.E.D.\) - 令\(x=\cos\frac{2}{5}\pi+\cos\frac{4}{5}\pi,y=\cos\frac{2}{5}\pi-\cos\frac{4}{5}\pi\)
\(x\cdot y=\cos^2\frac{2}{5}\pi-\cos^2\frac{4}{5}\pi=\frac{1}{2}(1+\cos\frac{4}{5}\pi)-\frac{1}{2}(1+\cos\frac{5}{8}\pi)\)
\(=\frac{1}{2}(\cos\frac{4}{5}\pi-\cos\frac{8}{5}\pi)=-\frac{1}{2}y\)
\(\Rightarrow x=-\frac{1}{2}\)