无约束优化
\(\begin{equation}\begin{split}\min f(\mathtt{x})\end{split}\end{equation}\)
\(\mathtt{x}\in{R^d}\)
- 可以令\(f(x)\)对向量\(\mathtt{x}\)求偏导,使得\(\nabla f(\mathtt{x})=0\)的向量\(\mathtt{x'}\)即为极值点
红色点标记的就是极值点
极值点一定包含极小值,但极值点往往不唯一,所以需要代入验证
- 利用梯度下降等办法获取迭代解
一个点的梯度方向意味着函数增长最快的方向,反过来说梯度方向的反方向是函数下降最快的方向
随机从一个点开始,每次沿着梯度方向的反方向走一小步,直到梯度足够小或者迭代次数到达上限结束迭代获得迭代解
\(\mathtt{x}_1=\mathtt{x}_0-\alpha\nabla{f(\mathtt{x}_0)}\)
这里\(\alpha\)控制移动的幅度大小,称为学习速率
梯度下降也会遇到局部最优解,要解决这个问题可以通过随机生成起始点进行多次梯度下降算法,从中选取最优的一个
左边箭头所指的是全局最优解,右边箭头所指的是局部最优解,
等式约束(拉格朗日乘数法)
拉格朗日乘数法是一种寻找多元函数在其变量受到一个或多个条件的约束时的极值的方法。这种方法可以将一个有n个变量与k个约束条件的最优化问题转换为一个解有n + k个变量的方程组的解的问题。这种方法中引入了一个或一组拉格朗日乘子,它们是在转换后的方程,即约束方程中作为梯度的线性组合中各个向量的系数。
假设\(\mathtt{x}\)是一个d维向量,从几何上看就是从\(h_i(\mathtt{x})=0\)这个\(d-1\)维曲面上寻找目标函数的最小值
\(\begin{equation}\begin{split}\min \quad&f(\mathtt{x})\\s.t.\quad &h_i(\mathtt{x})=0,i=1,2,...,k\end{split}\end{equation}\)
- 极小值落在约束之上
\(h_i(\mathtt{x})=0,i=1,2,...,k\)
此时等同于无约束优化
- 极小值未落在约束之上(黑色是\(\nabla f(x)\)绿色是\(\nabla h(x)\))
约束曲面上任一点梯度\(\nabla h(\mathtt{x})\)正交于约束曲面,最优点\(\mathtt{x^*}\)在曲面的梯度必定正交于约束曲面\(\nabla f(\mathtt{x})\)
在单约束条件下,\(\nabla f(x)\)和\(\nabla h(x)\)的梯度方向在同一直线上;多约束下,\(\nabla f(x)\)和\(\sum_{i=0}^k\mu_i\nabla h(x)\)即\(\nabla h(x)\)的梯度的线性组合方向在同一直线上,否则沿着约束向某一方向移动可以使得\(f(\mathtt{x})\)更小,即
\(\nabla f(\mathtt{x}^{*})=\lambda\sum_{i=0}^k\mu_i \nabla h_i(\mathtt{x}^{*})=\sum_{i=0}^k\lambda_i \nabla h_i(\mathtt{x}^{*}),\lambda_i\ne0\)
\(h_i(\mathtt{x^*})=0,i=1,2,...,k\)
将两种情况合起来得到方程
\(L\)(\(\mathtt{x,\lambda}\))=\(f(\mathtt{x})+\sum_{i=1}^k\lambda_ih_i(\mathtt{x})\),\(\lambda\)称为拉格朗日乘子
最优解\(\mathtt{x^*}\)满足
\(h_i(\mathtt{x^*})=0,i=1,2,...,k\)
不难发现\(L\)(\(\mathtt{x,\lambda}\))对\(\mathtt{x}\)求偏导置零正好是情况2,如果\(h_i(\mathtt{x})=0,i=1,2,...,k\),\(L\)(\(\mathtt{x,\lambda}\))=\(f(x)\),正好是无约束优化,所以原问题转化为对拉格朗日函数\(L\)(\(\mathtt{x,\lambda}\))的无约束化问题
拉格朗日乘数法所得的极点会包含原问题的所有极值点,但并不保证每个极值点都是原问题的极值点。
不等式约束(KKT)
\(\begin{equation}\begin{split}\min \quad&f(\mathtt{x})\\s.t.\quad &g_i(\mathtt{x})\le0,i=1,2,...,l\end{split}\end{equation}\)
- 极小值位于不等式约束之中
此时以下成立
\(g_i(\mathtt{x})\le0,i=1,2,...,k\)
这等同于无约束优化,可以直接通过条件\(\nabla f(\mathtt{x})=0\)来得到最优点
- 极小值位于不等式约束边界上
边界上的点梯度\(\nabla f(\mathtt{x})\)必定指向绿色区域内,而梯度\(\nabla g(\mathtt{x})\)必定指向绿色区域外,即\(\nabla f(\mathtt{x})\)和\(\nabla g(\mathtt{x})\)必须方向相反,否则沿着约束向某一方向移动可以使得f(x)更小,即
\(\nabla f(\mathtt{x}^{*})+\sum_{i=0}^l\lambda_i \nabla g_i(\mathtt{x}^{*})=0,\lambda_i\ge0\)
将两种情况合起来得到方程
\(L\)(\(\mathtt{x,\lambda}\))=\(f(\mathtt{x})+\sum_{i=1}^l\lambda_ig_i(\mathtt{x})\),\(\lambda\ge0\)
最优解\(\mathtt{x^*}\)满足KKT条件:
\[ \begin{cases} \ g_i(\mathtt{x^*})\le0;\\ \ \lambda_i\ge0;\\ \ \lambda_ig_i(\mathtt{x^*})=0;\\ \end{cases} \]
等式不等式混合约束
\(\begin{equation}\begin{split}\min \quad&f(\mathtt{x})\\s.t.\quad &h_i(\mathtt{x})=0,i=1,2,...,m\\&g_i(\mathtt{x})\le0,i=1,2,...,n\end{split}\end{equation}\)
\(L\)(\(\mathtt{x,\lambda,\mu}\))=\(f(\mathtt{x})+\sum_{i=1}^m\lambda_ih_i(\mathtt{x})+\sum_{i=1}^n\mu_ig_i(\mathtt{x})\)
最优解\(\mathtt{x^*}\)满足KKT条件:
\[ \begin{cases} \ g_i(\mathtt{x^*})\le0,h_i(\mathtt{x^*})=0;\\ \ \mu_i\ge0;\\ \ \mu_ig_i(\mathtt{x^*})=0;\\ \end{cases} \]
对偶问题
原问题
\(\begin{equation}\begin{split}\max \quad&z=\mathtt{c^Tx}\\s.t.\quad &\mathtt{Ax\le b}\\&\mathtt{x_i}\ge0,i=1,2,...,n\end{split}\end{equation}\)
对偶问题
\(\begin{equation}\begin{split}\min \quad&w=\mathtt{y^Tb}\\s.t.\quad &\mathtt{A^Ty\ge c}\\&\mathtt{y_i}\ge0,i=1,2,...,n\end{split}\end{equation}\)
假如原问题是工厂最大化利润,那么对偶问题就可以使最小化原材料用量
对偶理论
对称性
对偶问题的对偶是原问题
弱对偶性
原问题(max)的任意一个目标值不超过对偶问题(min)的任意一个目标值,也就是说对偶问题给出原问题的下界
无界性
原问题(max)为无穷大,则对偶问题(min)无可行解.当原问题(max)不可行,则对偶问题可能无界,也可能不可行
原问题有最优解,则对偶问题也存在最优解且相等
原问题的某个解对应目标值与对偶问题的某个解对应目标值相等则说明这是最优解
互补松弛性
针对以下问题分析
\(\begin{equation}\begin{split}\min \quad&f(\mathtt{x})\\s.t.\quad &h_i(\mathtt{x})=0,i=1,2,...,m\\&g_i(\mathtt{x})\le0,i=1,2,...,n\end{split}\end{equation}\)
拉格朗日函数
\(L\)(\(\mathtt{x,\lambda,\mu}\))=\(f(\mathtt{x})+\sum_{i=1}^m\lambda_ih_i(\mathtt{x})+\sum_{i=1}^n\mu_ig_i(\mathtt{x})\)
最优解\(\mathtt{x^*}\)满足KKT条件:
\[ \begin{cases} \ g_i(\mathtt{x^*})\le0,h_i(\mathtt{x^*})=0;\\ \ \mu_i\ge0;\\ \ \mu_ig_i(\mathtt{x^*})=0;\\ \end{cases} \]
容易理解对于满足约束的\(\mathtt{x}\)来说(满足约束即\(h_i(\mathtt{x})=0,g_i(\mathtt{x})\le0\),首先\(\sum_{i=1}^m\lambda_ih_i(\mathtt{x})=0\),又因为\(\mu_i\ge0\),所以\(\sum_{i=1}^n\mu_ig_i(\mathtt{x})\le0\),最大化也就是等于0)
\(\max\limits_{\mu_i>0,\lambda}L(\mathtt{x,\lambda,\mu})=f(x)\)
不满足则会趋于无穷
\(\max\limits_{\mu_i>0,\lambda}L(\mathtt{x,\lambda,\mu})=+\infin\)
原始问题就等价于
\(\min\limits_{\mathtt{x}}\max\limits_{\mu_i>0,\lambda}L(\mathtt{x,\lambda,\mu})\)
其对偶问题
\(\max\limits_{\mu_i>0,\lambda}\min\limits_{\mathtt{x}}L(\mathtt{x,\lambda,\mu})\)
对偶问题给出了原问题的下界,即
\(\max\limits_{\mu_i>0,\lambda}\min\limits_{\mathtt{x}}L(\mathtt{x,\lambda,\mu})\le\min\limits_{\mathtt{x}}\max\limits_{\mu_i>0,\lambda}L(\mathtt{x,\lambda,\mu})\)
\(\min\limits_{\mathtt{x}}\max\limits_{\mu_i>0,\lambda}L(\mathtt{x,\lambda,\mu})\)的第一要务是满足约束,第二要务才是最小化函数,而\(\max\limits_{\mu_i>0,\lambda}\min\limits_{\mathtt{x}}L(\mathtt{x,\lambda,\mu})\)第一要务是最小化函数,第二要务才是满足约束
如果目标是找唱歌最差(目标)的计算机学院的学生(约束),\(\min\limits_{\mathtt{x}}\max\limits_{\mu_i>0,\lambda}L(\mathtt{x,\lambda,\mu})\)相当于先找出所有计算机学院的学生,然后从中选出唱歌最差的学生,\(\max\limits_{\mu_i>0,\lambda}\min\limits_{\mathtt{x}}L(\mathtt{x,\lambda,\mu})\)相当于先从全校选出唱歌差的学生,然后从中选出计算机学院的学生.由于后者学生范围大,自然唱歌要更差些,这就是下界
显而易见由以上例子可以看出对偶问题和原问题的解不一定相同,两者之间的差距称作对偶误差,大部分对偶问题满足弱对偶性,假如对偶误差为0(即原问题和对偶问题同解),则称这种性质称为强对偶性
往往对偶问题更容易解决
slater条件
存在\(\mathtt{x}\).使得不等式约束\(g_i(\mathtt{x}),i=1,...n\)严格成立
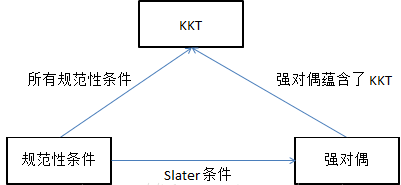
当强对偶条件满足就可以通过对偶问题解决原问题