题意:F(0)=1,F(1)=1,F(n)=3*F(n-1)+2*F(n-2) (n>=2) ,F(n) mod 998244353。给出Q跟N1,Ni=Ni-1^(F(Ni-1)*F(Ni-1)),求F(N1)^F(N2)^...^F(NQ)
这个比赛的E跟H数据都水得很,但题还是不错的。
比赛时是求了个循环节,又进行了矩阵的降幂,然后本地+测试在时限内跑出了几组1e7的数据,才敢交的,但没想到数据那么水,矩阵快速幂+map记忆化一下就能过。

1 #include<cstdio> 2 #include<tr1/unordered_map> 3 using namespace std; 4 typedef long long ll; 5 const int N=1e7+11,md=998244353; 6 tr1::unordered_map<ll,int> mmp; 7 ll aa[N],f[N]; 8 struct Matrix{ 9 int r,c; 10 ll a[5][5]; 11 Matrix(){} 12 Matrix(int r,int c):r(r),c(c){ 13 for(int i=0;i<r;i++) 14 for(int j=0;j<c;j++) a[i][j]=0; 15 } 16 }; 17 Matrix mmul(Matrix m1,Matrix m2,ll z){ 18 Matrix ans(m1.r,m2.c); 19 for(int i=0;i<m1.r;i++) 20 for(int j=0;j<m2.c;j++) 21 for(int k=0;k<m1.c;k++){ 22 ans.a[i][j]+=m1.a[i][k]*m2.a[k][j]%z; 23 if(ans.a[i][j]>=z) ans.a[i][j]-=z; 24 } 25 return ans; 26 } 27 Matrix mpow(Matrix m1,ll y,ll z){ 28 Matrix ans(m1.r,m1.c); 29 for(int i=0;i<ans.r;i++) ans.a[i][i]=1; 30 while(y){ 31 if(y&1) ans=mmul(ans,m1,z); 32 m1=mmul(m1,m1,z); 33 y>>=1; 34 } 35 return ans; 36 } 37 38 int main(){ 39 f[0]=0;f[1]=1; 40 for(int i=2;i<N;i++) f[i]=(f[i-1]*3ll%md+f[i-2]*2ll%md)%md; 41 int q,pos1,pos2,len,num,yu; 42 ll n,m,ans; 43 while(~scanf("%d%lld",&q,&n)){ 44 ans=aa[0]=0; 45 mmp.clear(); 46 pos1=pos2=-1; 47 for(int i=1;i<=q;i++){ 48 if(n<N) aa[i]=f[n]; 49 else{ 50 m=n-1; 51 if(m>=md-1) m%=md-1; 52 Matrix A(2,1),T(2,2); 53 A.a[0][0]=1; 54 T.a[0][0]=3;T.a[0][1]=2;T.a[1][0]=1; 55 T=mpow(T,m,md); 56 A=mmul(T,A,md); 57 aa[i]=A.a[0][0]; 58 } 59 if(n==0) break; 60 if(mmp[n]){ 61 pos1=mmp[n]; 62 pos2=i; 63 break; 64 } 65 else mmp[n]=i; 66 ans^=aa[i]; 67 n=n^(aa[i]*aa[i]); 68 aa[i]^=aa[i-1]; 69 } 70 if(pos1!=-1){ 71 len=pos2-pos1; 72 num=(q-pos2+1)/len; 73 yu=(q-pos2+1)%len; 74 if(num&1) ans^=aa[pos2-1]^aa[pos1-1]; 75 if(yu) ans^=aa[pos1+yu-1]^aa[pos1-1]; 76 } 77 printf("%lld\n",ans); 78 } 79 return 0; 80 }
但其实自己想一下,Q等于1e7,中间再套log的话,还有算矩阵快速幂时的一些常数,很明显就会T掉,水过去之余还是来学一些O(1)的处理方法。
首先这个数列显然是个线性递推数列,那么我们就可以求它的一个通项公式,具体求法360百科有好几个,我直接学习了第一个,方法:利用特征方程(线性代数解法)的解法。

特征方程的概述
一个数列:X(n+2)=C1X(n+1)+C2Xn
设r,s使X(n+2)-rX(n+1)=s[X(n+1)-rXn]
所以X(n+2)=(s+r)X(n+1)-srXn
C1=s+r
C2=-sr
消去s就导出特征方程式 r*r-C1*r-C2=0
我们把C1=3,C2=2代入就有可以解除r=(3+√17)/2,s=(3-√17)/2
然后F(n)=x1*rn+x2*sn,我们把F(0)=0,F(1)=1,代入就能解得x1=1/√17,x2=-1/√17
那么上诉数列的通项公式就是F(n)=1/√17*(((3+√17)/2)n-((3-√17)/2)n)
这个解法包含不少线性代数的知识,不明白的可以去学一下那个待定系数等比数列求法,或者看一下这个斐波那契数列通项公式是怎样推导出来的?,里面有矩阵的推导过程。
回到这题,我们有了通项公式,√17的话,前面的博客就有讲到二次剩余,那么通过x2≡17(mod 998244353)可以求出x来代替√17,然后里面的除法我们可以求逆元,这些都可以先求出了。
相关代码如下:

1 #include<cstdio> 2 #include<ctime> 3 #include<cstdlib> 4 #include<algorithm> 5 using namespace std; 6 const int md=998244353; 7 typedef long long ll; 8 struct Fp2{ 9 ll x,y; 10 }; 11 ll w; 12 Fp2 fmul(const Fp2 &f1,const Fp2 &f2){ 13 Fp2 ans; 14 ans.x=(f1.x*f2.x%md+f1.y*f2.y%md*w%md)%md; 15 ans.y=(f1.x*f2.y%md+f1.y*f2.x%md)%md; 16 return ans; 17 } 18 Fp2 fpow(Fp2 x,ll y){ 19 Fp2 ans; 20 ans.x=1;ans.y=0; 21 while(y){ 22 if(y&1) ans=fmul(ans,x); 23 x=fmul(x,x); 24 y>>=1; 25 } 26 return ans; 27 } 28 ll poww(ll x,ll y){ 29 ll ans=1; 30 while(y){ 31 if(y&1){ 32 ans*=x; 33 if(ans>=md) ans%=md; 34 } 35 x*=x; 36 if(x>=md) x%=md; 37 y>>=1; 38 } 39 return ans; 40 } 41 ll cipolla(ll x){ 42 if(x==0) return 0; 43 if(x==1) return 1; 44 if(poww(x,(md-1)>>1)+1==md) return -1; 45 ll a; 46 while(true){ 47 a=rand()%md; 48 w=((a*a%md-x)%md+md)%md; 49 if(poww(w,(md-1)>>1)+1==md) break; 50 } 51 Fp2 ans; 52 ans.x=a;ans.y=1; 53 ans=fpow(ans,(md+1)>>1); 54 return ans.x; 55 } 56 int main(){ 57 srand(time(NULL)); 58 ll py17=cipolla(17),nv2=poww(2,md-2); 59 printf("根号17的二次剩余:%lld\n",py17); 60 printf("2的逆元:%lld\n",nv2); 61 printf("根号17的二次剩余的逆元:%lld\n",poww(py17,md-2)); 62 printf("3+根号7除2:%lld\n",((3+py17)%md*nv2%md)%md); 63 printf("3-根号7除2:%lld\n",(((3-py17)%md+md)%md*nv2%md)%md); 64 return 0; 65 }
其中一组结果:
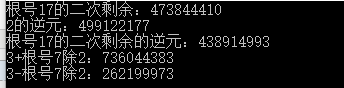
那么这时,我们设aa=736044383,bb=262199973,我们快速幂就可以log求出F(n)
但这还不够,我们需要的是O(1),所以我们可以先分块预处理。
怎么做呢,这时的aa,bb在 mod 998244353的意义下,已经是整数了,所以求aan或者bbn在n很大时,就可以进行我们前面指数循环节里的欧拉降幂了,也就是n=n%998244352+998244352(998244352是998244353是欧拉函数)
这时n最大是1996488703,√1996488703=44682.084810357719028060186400879,那么我们可以把5e4(大于等于44683)为一组分块,这样我们先预处理出aa跟bb的0次幂,1次幂,到5e4次幂,然后再预处理0*5e4次幂,1*5e4次幂到5e4*5e4次幂
那么当我们要求aa或者bb的n次幂时其实就是求(n/5e4)(整除)*5e4次幂 * n%5e4次幂,也就是设N=5e4,那么 n=q*N+r,q=n/N,r=n%N
这样我们就可以在O(1)求出相应的F(n),

1 #include<cstdio> 2 typedef long long ll; 3 const int N=5e4,md=998244353; 4 const ll nv17=438914993,aa=736044383,bb=262199973; 5 typedef long long ll; 6 ll a[N+11],af[N+11],b[N+11],bf[N+11]; 7 void init(){ 8 a[0]=b[0]=1; 9 for(int i=1;i<=N;i++){ 10 a[i]=a[i-1]*aa; 11 if(a[i]>=md) a[i]%=md; 12 b[i]=b[i-1]*bb; 13 if(b[i]>=md) b[i]%=md; 14 } 15 af[0]=bf[0]=1; 16 for(int i=1;i<=N;i++){ 17 af[i]=af[i-1]*a[N]; 18 if(af[i]>=md) af[i]%=md; 19 bf[i]=bf[i-1]*b[N]; 20 if(bf[i]>=md) bf[i]%=md; 21 } 22 } 23 int main(){ 24 init(); 25 int q; 26 ll n; 27 while(~scanf("%d%lld",&q,&n)){ 28 ll ans=0,fn,m; 29 while(q--){ 30 if(n==0) break; 31 m=n; 32 if(m>=md-1) m=m%(md-1)+(md-1); 33 fn=((af[m/N]*a[m%N])%md)-((bf[m/N]*b[m%N])%md); 34 fn=(fn%md+md)%md; 35 fn*=nv17; 36 if(fn>=md) fn%=md; 37 ans^=fn; 38 n=n^(fn*fn); 39 } 40 printf("%lld\n",ans); 41 } 42 return 0; 43 }
但由于数据的问题,预处理在计蒜客上实际运行时间还没直接套矩阵快速幂的快,自己出几个大数据就可看出哪个更快了,但我们不要被数据影响了,学到东西才是关键了。
总的来说,这题涉及到了线性递推数列的通项公式,二次剩余,逆元,还有分块思想,是个很不错的题。
