2322. 「清华集训 2017」Hello world!
题意
一棵树每个点有点权,每次可以选择两个点\(s, t\),选择步长为\(k\),从\(s\)跳到\(t\)(不足\(k\)步直接到\(t\)),并且有两种操作,一种是将经过所有点的点权都开根后下取整,一种是统计经过所有点的点权和。
点数\(\leq 50000\);
询问\(\leq 400000\);
点权\(\in [1, {10} ^ {13}]\)。
题解
考虑在一个序列上的做法。这个开根号本来就是一个经典操作。
可以考虑对步长\(k\)大小分块。设阈值为\(S\)。
如果\(k \geq S\),则考虑直接暴力跳,暴力修改,有效的修改最多\(\mathcal O(n \log \log V)\)次,如果一个数变成了1,就用并查集维护他所在的连续的1\(的最后位置(就是维护一段连续的1)。 如果\)k < S\(,则考虑建立\)k$个树状数组,查询修改都要依赖这个树状数组(包括上一种情况的修改,同时也要更新树状数组)。
如果把并查集复杂度当做常数,则复杂度是 \(\mathcal O(n \log \log V S \log n + Q \frac{n}{S} \log n + Q S \log n)\)。
考虑在树上做,就要支持查询某一个节点的\(k\)级祖先,我们把一个原图的极大子集叫做\(k\)级树当且仅当它是一棵树,且父子节点在原树上距离为\(k\)。
考虑从\(s\)到\(t\)的路径要分解成两段竖直路径(一端是另一端的祖先的路径),然后对于每一段路径上的点,都是\(k\)级树上的一条连续路径。
前一种情况还是可以用类似方法做,变化不大;
后一种情况,要在对应\(k\)级树上修改或查询某段路径的权值。这个可以直接无脑树剖,也可以用树上差分做。(实测树剖更快。。。)
若使用树上差分,复杂度为 \(\mathcal O(n \log \log V S \log n + Q \frac{n}{S} \log n + Q S \log n)\)。
实测\(S\)取20时最优。。(咋看都不像,都是常数惹的祸)
另外吐槽一句,树上差分什么的竟然没有想到,看来已经不会了。。
2323. 「清华集训 2017」小 Y 和地铁
2324. 「清华集训 2017」小 Y 和二叉树
2326. 「清华集训 2017」简单数据结构
题意
一个序列,支持四种操作:
1.在左端加入一个数;
2.在右端加入一个数;
3.删除最左端的数;
4.删除最右端的数;
求每个操作后最长上升倍数子序列的长度和不同的开头数。
保证每个操作前后序列非空,每种数只会出现在一个位置上。一个数出现次数不超过10。
数的大小是\({10} ^ 6\)级别的。
题解
一看就是套路题。先预处理一个数的倍数和约数。总和是\(\mathcal O(m \log m)\)级别的。
注意到一个数同时只会在一个位置出现,很显然可以以位置为某个数的标记。
考虑dp数组\(dp_i\)表示以\(i\)位置开头的最长上升倍数子序列的长度,\(f_{i, j}\)为以\(i\)位置开头,上一个位置的dp值为\(j\)的个数。注意到我们要求的子序列长度在\(\mathcal O(\log n)\)级别,所以可以这么做。
设\(\sigma(n)\)表示\(n\)的因子数,\(\tau(n)\)表示\(n\)的倍数数(\(m\)以内)。
对于操作1,直接维护当前加入的位置的信息即可,复杂度\(\mathcal O(\sigma(x) + \log m)\)。
对于操作2,考虑把所有有影响的数取出并按照位置为关键字排序,依次更新dp值和f数组(注意顺序一定要对),由于所有有影响的数一定是加入的数的倍数,所以复杂度为\(\mathcal O(\tau(x) (\log m + \log n) + \sum_{x | g} \tau(g) + \log m)\)。
对于操作3,和1类似,直接删除这个位置的信息即可,复杂度\(\mathcal O(\log M)\)。
对于操作4,和2类似,\(\mathcal O(\tau(x) (\log m + \log n) + \sum_{x | g} \tau(g) + \log m)\)。
由于有每个数最多出现10次的保证,所以总复杂度还是可以的。
2328. 「清华集训 2017」避难所
题意
在\(b\)进制下,找一个数,满足\(f(n) > n\)。
\(f(n)\)由递归定义
\[ f(n) = \begin{cases} f(\frac {n}{k}) * b + k, n \geq b & k = \max \{k_0: k_0 | n \cap k_0 < b \} \\ n, n < b \\ \end{cases} \]
如果最小的\(n\)在十进制下超过\({10} ^ {18}\),输出-1。
题解
结论题……(还是我菜了)
注意到当\(b\)足够大时,取
\(x\)使得\((x - 1) ^ 2 \leq b \cap x ^ 2 > b\),\(y\)使得\(y ^ 3 \leq b \cap (y + 1) ^ 3 > b\),
然后就找到了一个解\(n = \{x * y, x * y, x * y\}\)(对应的\(f(n) = \{y ^ 3, x, x, x\}\))。
注意到在\(b\)足够大时这是不错的,因为\(x * y \leq b\),而\(b \leq {10} ^ 5\),满足了\(n\)的各数位乘积不超过\({10} ^ {18}\)。
当\(b \leq 130\)时暴力找解即可(解的形式都是\(\{x, x, y\}\)或者\(\{x, y, y\}\),我也不知道为什么……)。
2330. 「清华集训 2017」榕树之心
题意
开始你在1号点(根),每次你可以选择一个未扩展节点\(v\),连上有关的边\((u, v)\)(满足\(u\)是已扩展节点),然后向\(v\)的方向移动一步。
问最后是否能停在某个节点上。
题解
2331. 「清华集训 2017」某位歌姬的故事
题意
给一些限制,表示一个区间\([l, r]\)内最大数为\(x\),所有数都在\([1, A]\)内,求合法序列的数量。
题解
如果没有\(x\)相同的情况,那就是个水题。
考虑一般解法。设\(c_i\)为位置\(i\)的最低限制。
按照\(c_i\)的大小,我们可以把原来的序列重新排序,如下图。
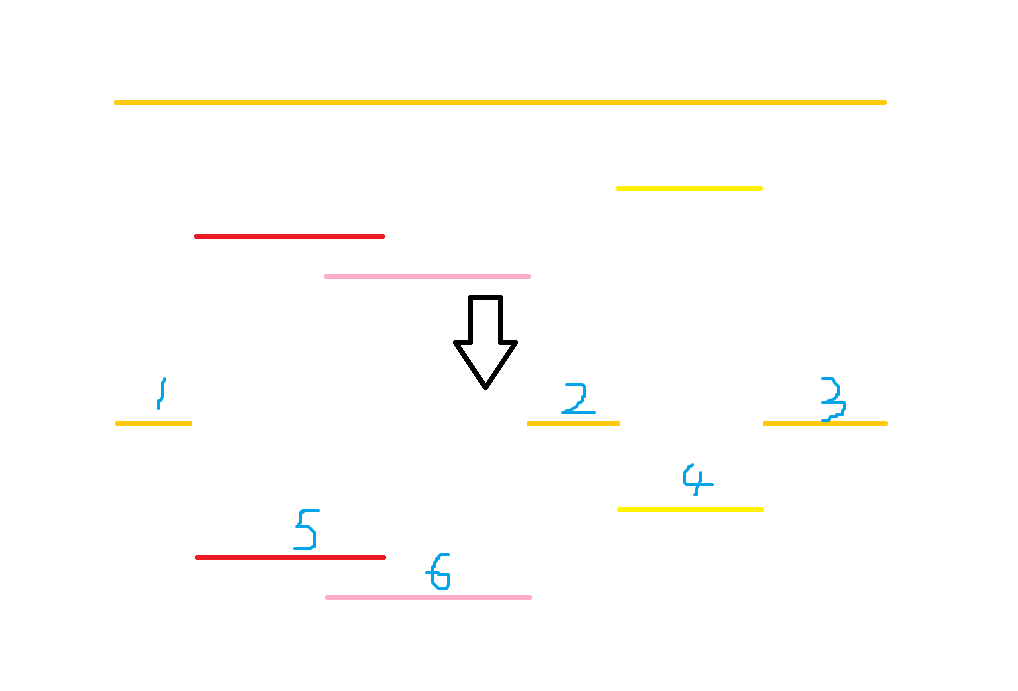
就像上图需要注意的是,重排后,1,2,3应该要归于同一限制的。反正这种东西写离散化也是烦的要死。
现在考虑一段相同高度的限制,如图。
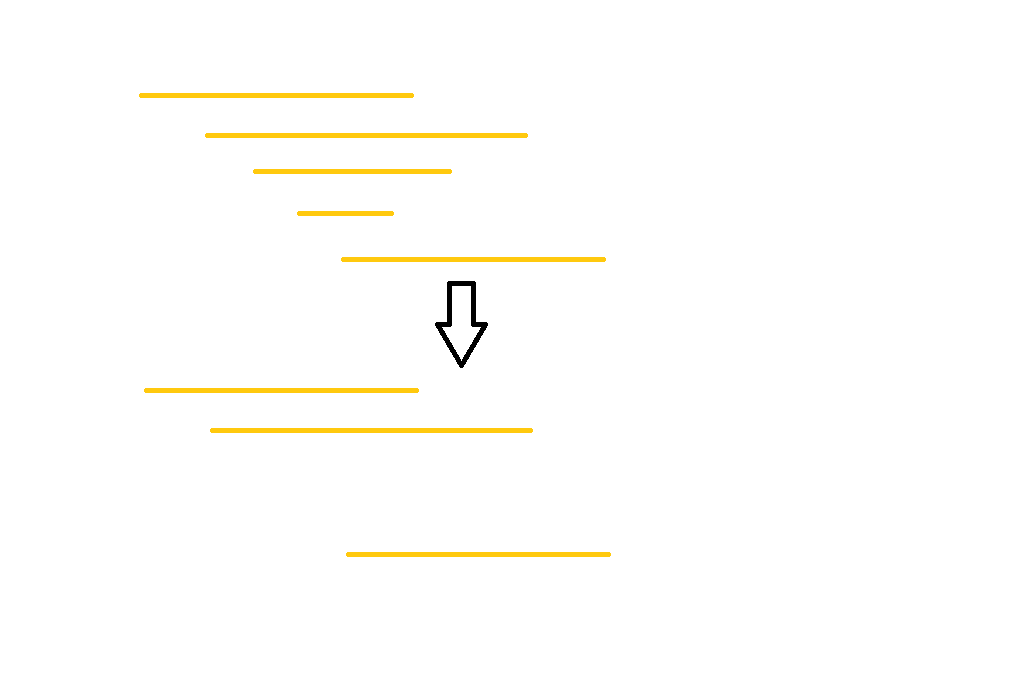
应该把无用区间删去,然后区间就是随左端点单调,右端点单调的了。
然后做个nmdp即可。。。(dp寥寥几行,预处理独领风骚)