关于机器学习的方法，大多算法都用到了最优化求最优解问题。梯度下降法（gradient descent)是求解无约束最优化问题的一种最常用的方法。它是一种最简单，历史悠长的算法，但是它应用非常广。下面作一下小总结：
一、梯度下降的初步认识
先理解下什么是梯度，用通俗的话来说就是在原变量的基础上每次迭代增加一定的量，比较各个变量下目标函数的大小。
例如有一个目标函数 y = 2χ2 ,那么求目标函数的最小值，我们先给x赋一个值-5，然后每次给x加一个值（有正负方向的值），这样y每次都会有一个值，当值减小幅度达到一定精确度时停止，这是的x就是我们求的最优解。
是不是有一点感觉了，上面的例子比较简单，通常在求解最优解的时候，目标函数就是我们要优化的，找出满足目标函数的最优解。有时候目标函数是比较复杂的，这时候梯度下降法就比较有用了。
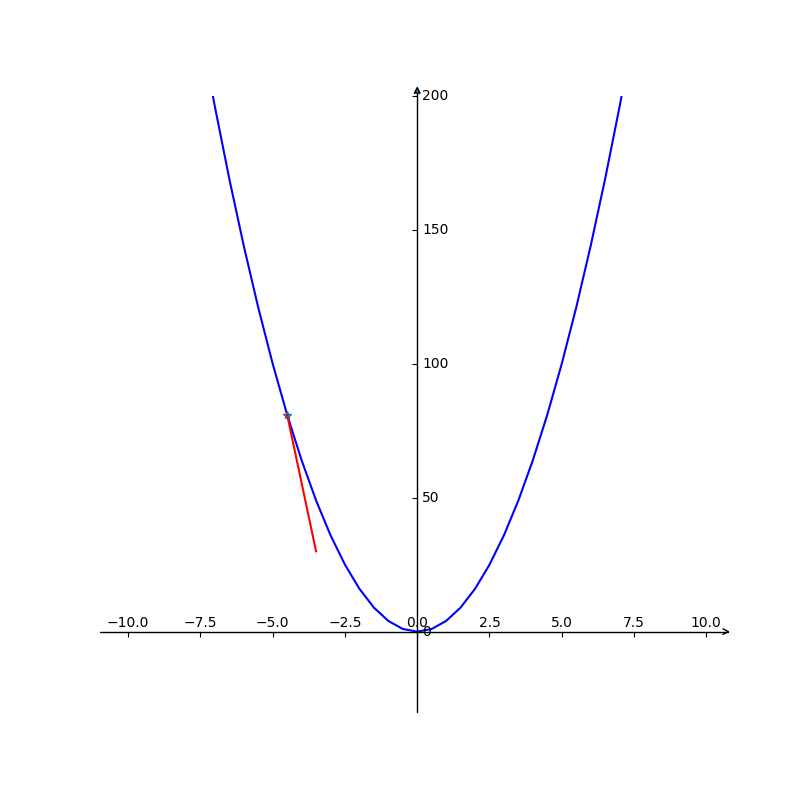
所谓梯度，如果目标函数可微，我们把目标函数的各个变量的偏导组成一个向量，既是梯度。主要是在优化过程中，我们怎么给变量增加还是减少的方向变量。如上例中我们怎么知道给x增加一定的量的，就是靠方向变量了。
二、梯度下降法的概念
梯度：即对变量的偏微分的组成的向量，（∂f/∂x1,∂f/∂x2 ...)。
步长：即每次迭代给变量增加的值，通常是一个值*梯度
梯度下降法就是沿着负方向迭代，直到找到最小值。
与之相反的是梯度上升法，沿着梯度正方向迭代。
梯度下降法的有缺点：
优点：实现比较简单，当目标函数是凸函数可以找到全局最优解。
缺点：容易陷入局部最优，靠近极小值时收敛速度会变慢，可能成之字下降，直线搜索可能会产生一些问题。
三、具体实现的算法例子
我们以逻辑回归的参数最大似然估计为例。
目标函数：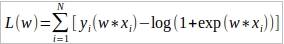
求目标函数的极大值。我们要对式中的w进行参数估计。
（1）我们这里初始化w1，w2 , ... wN 都为0
（2）计算梯度，即各个w的偏导∂L(w)/∂w
(3) gi+1= L(w)i+1-L(w)i ，i表示第i次迭代，gi+1代表第i+1次的目标函数和第i次的差
（4）对变量进行迭代 wij=wi+1j+∂L(w)i/∂wj ...
代入计算wij，再计算gi+1，若gi+1大于阈值，重复3、4，直至g小于阈值，既是我们要的最优解。
四、梯度下降算法的调优
1、步长。在设定步长的时候如果设置过大收敛较快但是可能错过最优解，步长太小收敛较慢。实际用法中可以根据样本进行决定。设置多组步长实验。
2、初始值。初始值不同不仅影响算法的收敛速度，还影响变量的是否陷入局部最优。需要多次用不同的初始值进行运算，选择目标最优的一组解。
3、特征归一化：由于不同的特征取值范围不一样，可能导致迭代很慢，可以参数归一化解决。
五、梯度下降算法的衍生
后面再补。。。