浅谈splay在区间问题中的应用

(笔者才疏学浅，如有疏漏还请各位不吝赐教)

1.从二叉搜索树谈起

首先，二叉搜索树是满足如下性质的二叉树

这棵二叉树的每一个结点都有一个权值$v$
对于二叉搜索树中的每个结点，如果它有左子树，那么它的左子树中的每一个结点的权值都小于这个结点本身的权值
对于二叉搜索树中的每个结点，如果它有右子树，那么它的右子树中的每一个结点的权值都大于这个结点本身的权值

下图就是一棵二叉搜索树(感谢EternalAlexander的OI Painter)

图中权值为5的结点的左子树权值分别为1,2,3,4，均小于5
右子树权值为6,7，均大于5
对于其他结点也满足这个优美的性质

为了加深大家对二叉搜索树的理解，我们来看一道题目:

维护一段没有重复元素的序列，支持以下两种操作:
1 $Insert(x)$ 插入元素 $x$
2 $Get(x) $ 输出第$x$小的数

对于操作1，我们需要找到$x$的正确插入位置，假设我们现在要将$x$插入到以$i$为根的子树(包括它本身)中，那么会有两种情况:

1.$x<tree[i].value$,说明$x$的位置在$i$的左子树中
2.$x>tree[i].value$,说明$x$的位置在$i$的右子树中

这样从根结点递归插入直到访问到空结点后插入即可

好了，现在我们解决了操作1，那么操作2该怎么办呢?

对于每个结点,我们维护一个$size$，表示以$i$为根的子树(包括$i$)的大小

那么假设我们现在要找以$i$为根的子树的第$k$小值，易知这棵子树中比$i$小的有$size[tree[i].leftson]$个，所以

如果$k<=size[tree[i].leftson]$，递归进入左子树查找
如果$k=size[tree[i].leftson]+1$，那么$i$结点就是我们要找的结点
如果都不是，那么递归进入右子树查找，此时$k$应该减去$size[tree[i].leftson]+1$

但是，一棵普通的二叉搜索树能解决的问题十分有限，当遇到删除操作时就已经变得很难受，还可能出现树退化成链的糟糕情况(可以想象一下插入一段递增的数)，单次操作的最坏复杂度可能会达到$O(n)$

而所谓平衡树，其实就是使原本形态可能不平衡的树尽量平衡，通过$rotate$等操作使树的深度达到优秀的$log n$，而$splay$就属于平衡树中的一种

还不会权值splay的同学请先看一下这位dalao的讲解~

2.区间Splay的基本性质

首先，我们类比之前二叉搜索树以及权值$splay$的性质，可以构造出如下的一棵树

对于树中的每个结点，如果它有左子树，那么它的左子树中的每一个结点在原序列中的位置都比这个结点靠前
对于树中的每个结点，如果它有右子树，那么它的右子树中的每一个结点在原序列中的位置都比这个结点靠后

举个例子，我们对${1,5,4,2,3}$建立区间$splay$

1.插入1

2.插入5，由于5的位置比2靠后，因此5插入到2的右儿子处

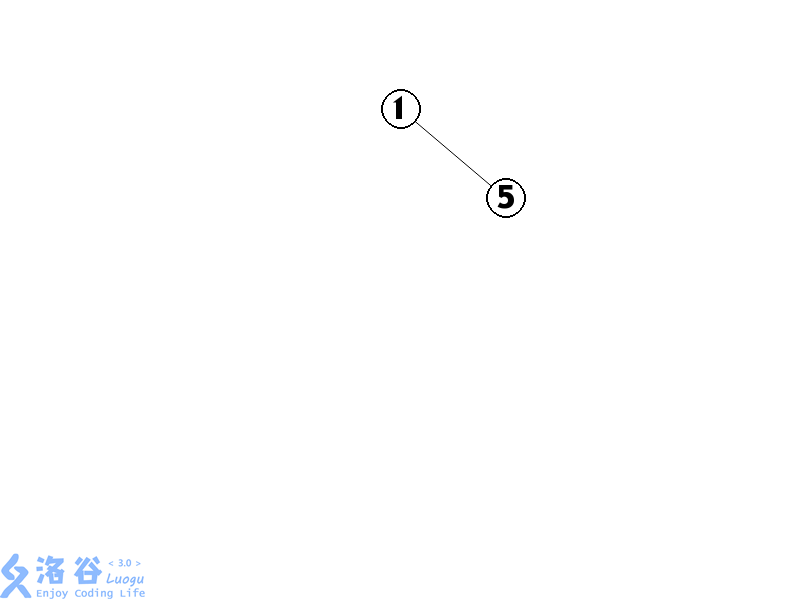
3.为了维护树的平衡，我们将5 $splay$到根结点

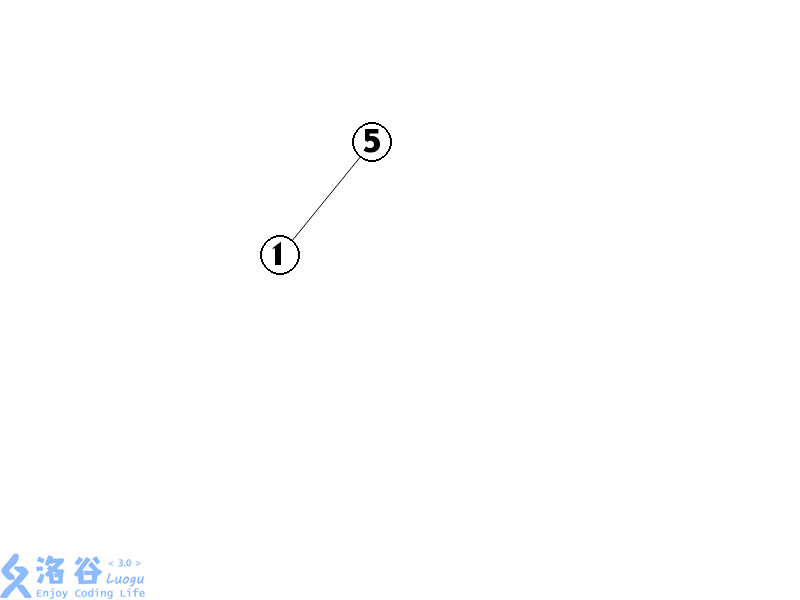
4.插入4,4的位置在5之后

5.同样，将4 $splay$到根

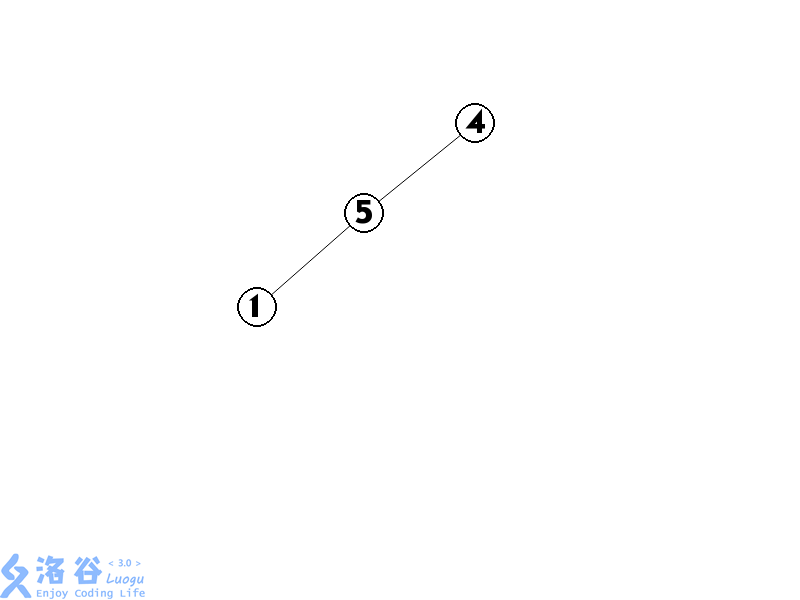
最后这棵树可能是这样的(为了好看我就先提前$splay$了)

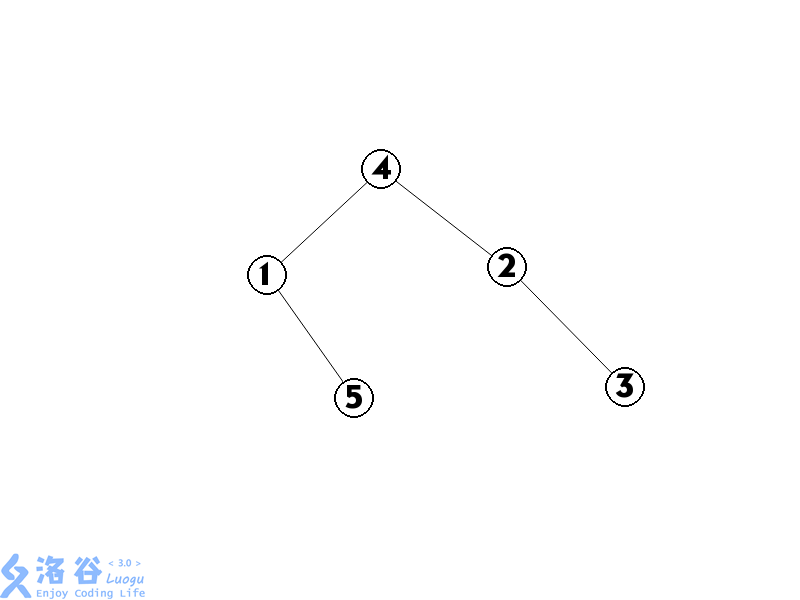
现在我们会发现一个重要的性质:对这棵splay进行中序遍历后得到的恰好是原序列

那么，如果我们把元素在原序列中的位置当做权值，区间splay其实就是一棵每个点的权值都可能动态变化的权值splay，至于为什么权值会变化，是因为这个数在序列中的位置可能发生了变化(比如翻转)

区间splay中，每个结点在储存它本身的信息外，还储存着它子树这段连续区间的信息，比如说上图中标号为1的结点可能除了存自己的value,size以外还存着1,5的value之和，4结点可能存着所有结点value的总和，通过这种信息合并可以像线段树一般大大缩短查询的复杂度

你可以这样认为:区间splay中每个结点代表的不只是它本身，还可以代表它的整颗子树

下面开始讲解一些具体操作:

Kth

区间splay中查找目前序列中第$k$位置上的数和二叉搜索树查找第$k$小是一摸一样的，代码如下:

int Kth(int x)
{
    int u=root;
    while(1)
    {
        if(t[u].tag)pushdown(u);//这东西之后解释
        if(x<=t[t[u].ch[0]].siz)u=t[u].ch[0];//ch[0],ch[1]分别是左儿子和右儿子，t[x].siz表示以x为根的子树的大小
        else if(t[t[u].ch[0]].siz+1==x)return u;
        else x-=(t[t[u].ch[0]].siz+1),u=t[u].ch[1];
    }
}

Pushup

将子树信息向上合并的函数，具体代码如下(以维护子树和 sum为例)

inline void pushup(int x)
{
    int l=t[x].ch[0],r=t[x].ch[1];
    t[x].sum=t[l].sum+t[r].sum+t[x].v;//一个结点子树之和sum=左子树sum+右子树sum+本身的value
    t[x].siz=t[l].siz+t[r].siz+1;
}

Split

就像LCT中的Access操作，区间splay的核心操作split就是提取一段区间$[l,r]$，具体操作就是先将$Kth(l-1)$旋转到根，再把$Kth(r+1)$旋转到根的右儿子，那么由于区间splay的中序遍历为原序列，现在$Kth(r+1)$的左子树就正好是$[l,r]$这段区间
代码如下:

int split(int l,int r)
{
    int x=Kth(l-1),y=Kth(r+1);
    splay(x,0),splay(y,x);
    return t[y].ch[0];
}//这样返回的就是代表一段区间[l,r]的结点编号

举个例子，假设还是刚才的${1,5,4,2,3}$这段序列，我们现在想要区间$[3,4]$的和
1 把Kth(3-1)即5旋转到根

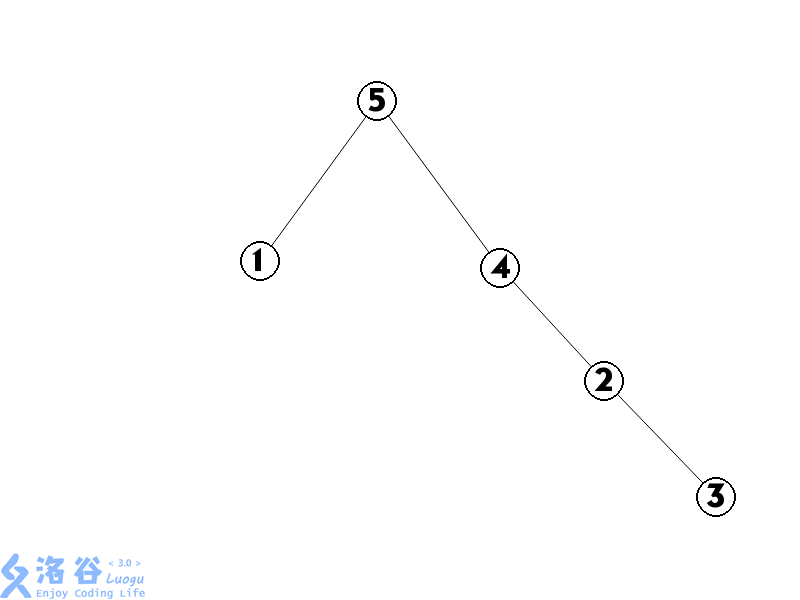
2 把Kth(4+1)即3旋转到根的右儿子

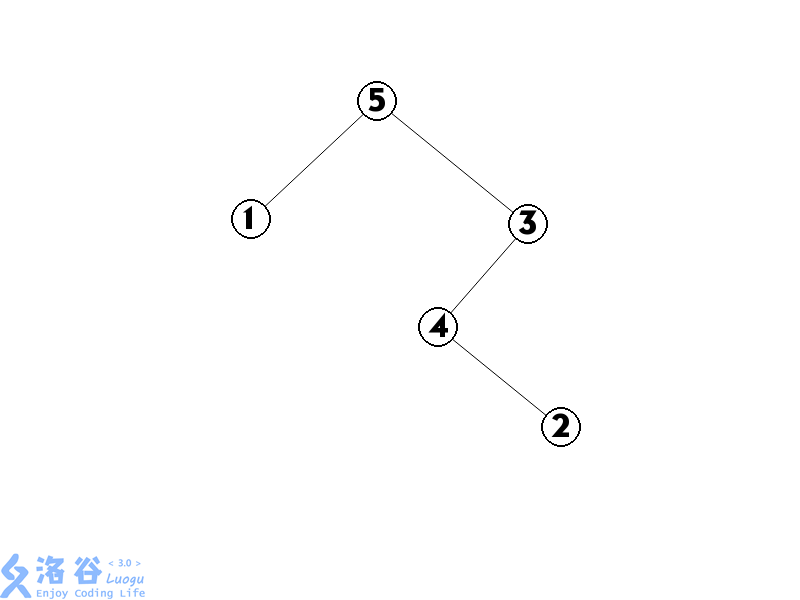
可以在上图中很明显的看出区间$[3,4]$即$4,2$这两个数就是现在3的左子树，既不少也不多，由于我们在每个结点存了子树和，所以3的左儿子的子树和$sum$就是我们要求的区间和

Insert

假设我们要将数k插入到第x个数后面，那么先$split(Kth(x),Kth(x+1))$后将x作为现在$Kth(x+1)$的左儿子就可以啦

Delete

和$Insert$操作一样，只不过是将$Kth(x+2)$的左儿子删去

Pushdown

现在考虑如何区间修改?
首先，如果我们要将区间$[l,r]$每个数加上$k$，那么肯定先要$split(l,r)$，将这段区间提取出来，之后怎么办?

打懒惰标记?那不是线段树吗?

答案是可以的，由于我们统计答案是自上而下的，所以可以在所有复合操作所共有的$Kth$操作中边访问下传标记，这样就能保证解的正确性

代码:(以区间统一赋值为k的标记为例)

inline void pushdown(int x)
{
    int l=t[x].ch[0],r=t[x].ch[1];
    if(t[x].tag)//是否有区间统一赋值的标记
    {
        t[x].tag=0;
        if(l)t[l].tag=1,t[l].v=t[x].v,t[l].sum=t[x].v*t[l].siz;//sum是维护的子树和
        if(r)t[r].tag=1,t[r].v=t[x].v,t[r].sum=t[x].v*t[r].siz;
    }
}

其实你会发现区间splay对于区间加，区间乘，区间赋值，区间Rmq问题的处理和线段树是一模一样的，大多数线段树都可以用区间splay代替，而区间splay能处理的问题会更多

区间splay的$rotate,splay$和权值splay并没有什么区别，这里不再赘述

下面看一道例题:

您需要写一种数据结构，来维护一个数列，其中需要提供以下操作：翻转一个区间，例如原序列是5 4 3 2 1，翻转区间是[2,4]的话，结果是5 2 3 4 1

首先构建区间splay，不难发现翻转一段区间$[l,r]$就是将代表这个区间的结点的子树中每一对左右子树都交换

区间操作肯定会想到打标记啦，只要用一个tag表示区间翻转的懒惰标记就可以了，下传标记就是左右子树的标记^=1,然后交换左右子树就好了

细节:这样如果修改区间$[1,n]$会出问题，所以加入两个哨兵结点$1,n+2$防止越界，那么我们的序列下标都+1就好了

这里是丑陋的代码~

const int maxn=100000+10;
struct node
{
    int ff,val;//父亲，权值
    int ch[2];//左右儿子
    int siz;//子树大小
    int tag;//翻转的懒惰标记
}t[maxn];
int tot,n,root,m;
inline void pushup(int x)//信息向上合并
{
    t[x].siz=t[t[x].ch[0]].siz+t[t[x].ch[1]].siz+1;
}
inline void pushdown(int x)//下传标记
{
    t[t[x].ch[0]].tag^=1,t[t[x].ch[1]].tag^=1;
    swap(t[x].ch[0],t[x].ch[1]);
    t[x].tag=0;
}
inline void rotate(int x)
{
    int y=t[x].ff,z=t[y].ff;
    int k=(t[y].ch[1]==x);
    t[z].ch[t[z].ch[1]==y]=x,t[x].ff=z;
    t[y].ch[k]=t[x].ch[k^1],t[t[x].ch[k^1]].ff=y;
    t[x].ch[k^1]=y,t[y].ff=x;
    pushup(y),pushup(x);
}
void splay(int x,int goal)
{
    while(t[x].ff!=goal)
    {
        int y=t[x].ff,z=t[y].ff;
        if(z!=goal)
            (t[y].ch[0]==x)^(t[z].ch[0]==y)?rotate(x):rotate(y);
        rotate(x);
    }
    if(goal==0)root=x;
}
void insert(int x)//插入第x个数
{
    int u=root,ff=0;
    while(u)ff=u,u=t[u].ch[x>t[u].val];
    u=++tot;
    if(ff)t[ff].ch[x>t[ff].val]=x;
    t[u].val=x,t[u].siz=1,t[u].ff=ff;
    t[u].tag=0,t[u].ch[0]=t[u].ch[1]=0;
    splay(u,0);
}
int Kth(int x)//查询序列中第x个数在splay中的位置
{
    int u=root;
    while(1)
    {
        if(t[u].tag)pushdown(u);
        if(x<=t[t[u].ch[0]].siz)u=t[u].ch[0];
        else if(t[t[u].ch[0]].siz+1==x)return u;
        else x-=(t[t[u].ch[0]].siz+1),u=t[u].ch[1];
    }
}
void solve(int l,int r)
{
    l=Kth(l),r=Kth(r+2);//相当于split(l,r)，由于有哨兵结点所以下标+1
    splay(l,0),splay(r,l);
    t[t[r].ch[0]].tag^=1;
}
void print(int x)
{
    if(!x)return;
    if(t[x].tag)pushdown(x);
    print(t[x].ch[0]);
    if(t[x].val>1&&t[x].val<n+2)printf("%d ",t[x].val-1);
    print(t[x].ch[1]);
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n+2;++i)insert(i);
    int l,r;
    for(int i=1;i<=m;++i)scanf("%d%d",&l,&r),solve(l,r);
    print(root);
}

3.一些习题

P3391 【模板】文艺平衡树（Splay）模板题QwQ
SPOJ4487 GSS6带插入区间最大子段和，同线段树一样 $pushup$ 区间信息即可
P2042 [NOI2005]维护数列操作比较多，且涉及到 $splay$ 的线性构造