FFT 本质上就是将系数表示法转化为点值表示法,再相乘后再转化为系数表示法。本来第一个转换要o2复杂度,第二个高斯消元要o3复杂度。但是由于虚数单位根的存在,可以降低复杂度至nlogn
相关文章链接:https://blog.csdn.net/GGN_2015/article/details/68922404
然而还是不懂怎么写fft,太复杂。
卢卡斯定理:https://blog.csdn.net/qq_40679299/article/details/80489761
结合费马小定理或拓展欧几里得定理可以对组合数取模。
快速幂公式:
快速幂算法依赖于以下明显的公式
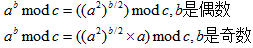
有了上述两个公式后,我们可以得出以下的结论:
1.如果b是偶数,我们可以记k = a^2 mod c,那么求(k)b/2 mod c就可以了。
2.如果b是奇数,我们也可以记k = a^2 mod c,那么求((k)b/2 mod c × a ) mod c =((k)b/2 mod c * a) mod c 就可以了。
nt ans = 1;
a = a % c;
if(b%2==1)
ans = (ans * a) mod c; //如果是奇数,要多求一步,可以提前算到ans中
k = (a*a) % c; //我们取a^2而不是a
for(int i = 1;i<=b/2;i++)
{
ans = (ans * k) % c;
}
ans = ans % c;
我们可以看到,我们把时间复杂度变成了O(b/2).当然,这样子治标不治本。但我们可以看到,当我们令k = (a * a) mod c时,状态已经发生了变化,我们所要求的最终结果即为(k)b/2 mod c而不是原来的ab mod c,所以我们发现这个过程是可以迭代下去的。当然,对于奇数的情形会多出一项a mod c,所以为了完成迭代,当b是奇数时,我们通过
ans = (ans * a) % c;来弥补多出来的这一项,此时剩余的部分就可以进行迭代了。
形如上式的迭代下去后,当b=0时,所有的因子都已经相乘,算法结束。于是便可以在O(log b)的时间内完成了。于是,有了最终的算法:快速幂算法。
以上摘自http://www.cnblogs.com/Howe-Young/p/4097277.html