一.FFT(Fast Fourier Transform)是什么
作者:肖畅
链接:https://www.zhihu.com/question/21314374/answer/542909849
来源:知乎
FFT是 Cooley & Tuket 两人1965年提出的快速计算DFT的算法。这背后还有个故事,美国和苏联1963年签了个核试验禁令,互相约定大家都不搞核试验了。但是美国不放心啊,怕毛子说一套做一套,肯尼迪就请了一堆科学家开会,说想搞一套不用去苏联检查就能探测到核试验的设备。美国在苏联周围放了一圈声波探测仪,但是遇到个问题——DFT算得太慢了。正巧 Tuket 和IBM的一个叫 Richard Garwin 的出席了那次会议。会上Garwin就想起来Tuket和Cooley好像合作过一个类似的算法,就让Tuket去找Cooley,但是隐藏了真实目的,告诉Cooley这个算法是为了探测氦3晶体的自旋周期……(也是醉了orz)。两人的算法最后于1965年发表,极大提升了DFT的计算速度,甚至被后世誉为“20世纪最伟大的工程算法”。
从DFT的公式可以看出其算法复杂度是 的,两人的FFT算法表明,在N为合数的情况下
,原长度为N的DFT可以分解为两个长度分别为
和
的DFT!
当然算法不停止于此,如果 和
还可以继续分解,就可以分解为更多小DFT来计算。
使用了算法中的分治(divide and conquer)策略。
而由于DFT的长度其实是可以任意选择的,因此通常在使用FFT时,都选择2的整数次幂作为FFT长度,这样可以一直分解到N/2个长度为2的DFT,复杂度直接降到 。
二.推导快速傅里叶变换基础知识
1.多项式

2.多项式的度数

3.多项式的线性空间

4.系数表达

5.向量的卷积

6.分治乘法


7.点值表达

8.插值

9.点值计算分析

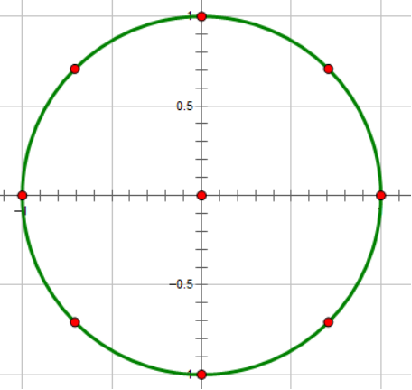
10. 单位复数根

11.单位复数根的性质
(1)消去引理
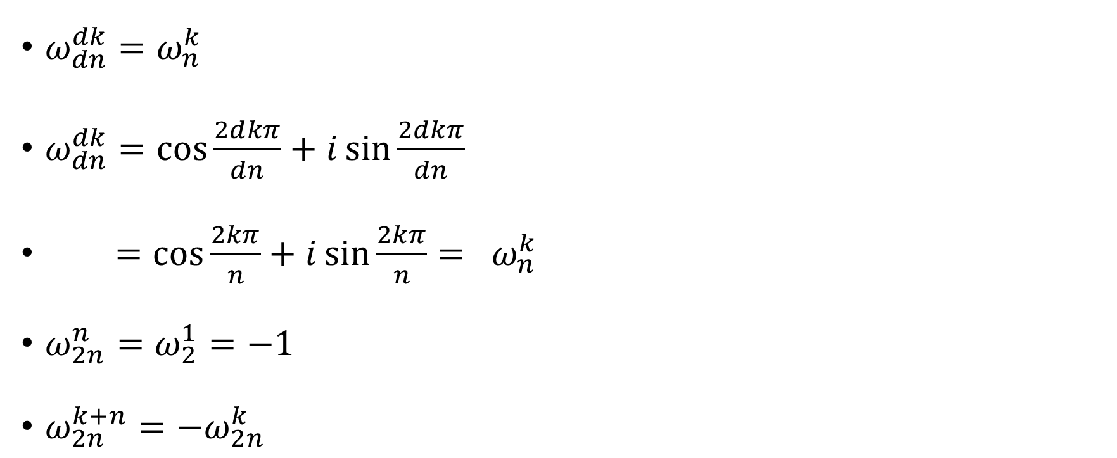
(2)折半引理

(3)求和引理
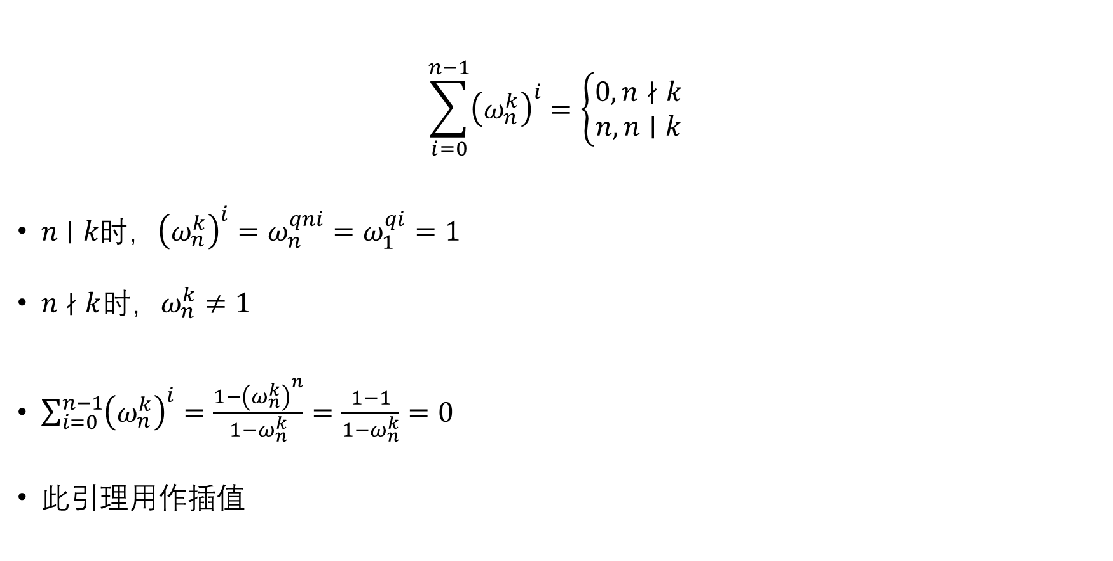
12.离散傅里叶变换(Discrete Fourier Transform 简称DFT)

13.多项式求值算法
给定多项式:
设为1的
次方根,即:
,对所有的
计算
的值。
算法一:蛮力算法
对每个做下述运算:依次计算每个项,
,
,对
求和。
对于每个的计算需要:
次乘法,所以进行n次
的计算需要进行
次乘法。
蛮力算法时间复杂度:。
算法二:改进的求值算法
利用前面的求值结果,依次对每个做下述计算:
每一次需要做一次乘法,一次加法,所以给定了一个,只需要进行
次乘法。
进行次
的计算需要进行
次乘法。
改进的求值算法时间复杂度:
算法三:偶系数与奇系数多项式
时:
一般公式(n为偶数):
也是1的
次根。
偶次数与奇次数多项式计算为规模的子问题,然后利用子问题的解
与
得到的
。
不需要重新计算,
也是1的
次根,也在单位圆上,隔一个取一个就可以找到。
注:本文整理网上资料,包括知乎、博客等,如有侵权立刻删除。