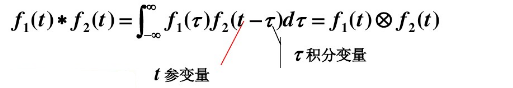一.卷积的定义

简单定义：

卷积是分析数学中一种重要的运算。

设: $f(x),g(x)$ 是 $R1$ 上的两个可积函数，作积分：

可以证明，关于几乎所有的实数 $x$ ，上述积分是存在的。这样，随着x的不同取值，这个积分就定义了一个新函数 $h(x)$ ，称为函数 $f$ 与 $g$ 的卷积，记为 $h(x)=(f*g)(x)$ 。

分析：

$\mathbf{h(x)=f(t)*g(t)=\int_{-\infty }^{\infty}f(\tau )*g(t-\tau)d\tau}$

（1）将 $f(t)$ 和 $g(t)$ 中的自变量由 $t$ 改为 $\tau$ ， $\tau$ 成为函数的自变量；

（2）把其中一个信号翻转、平移；

$\mathbf{g(\tau){\rightarrow}}h(-\tau)\rightarrow h(-(\tau-t))=h(t-\tau)$

（3）将 $f(\tau)$ 与 $g(t-\tau)$ ；对乘积后的图形积分。

二.信号与线性系统中的意义

首先，在提到卷积之前，必须提到卷积出现的背景。卷积是在信号与线性系统的基础上或背景中出现的，脱离这个背景单独谈卷积是没有任何意义的，除了那个所谓褶反公式上的数学意义和积分（或求和，离散情况下）。

信号与线性系统，讨论的就是信号经过一个线性系统以后发生的变化（就是输入输出和所经过的所谓系统，这三者之间的数学关系）。所谓线性系统的含义，就是，这个所谓的系统，带来的输出信号与输入信号的数学关系式之间是线性的运算关系。

对于线性系统来说，系统响应=零状态响应+零输入响应，并且零状态响应就是激励与系统函数的卷积，再加上零输入响应。

物理意义：

将信号分解成冲激信号之和，借助系统的冲激响应 $h(t)$ ，求出系统对任意激励信号的零状态响应，即：任意信号 $f(t)$ 可表示为冲激信号的加权和： $f(t)=\int_{-\infty }^{\infty}f(\tau )\delta (t-\tau)d\tau$ 。

若把它作用于冲激响应为 $h(t)$ 的LTI系统，则响应为：

$r(t)=H[f(t)]=H[\int_{-\infty }^{\infty}f(\tau )\delta (t-\tau)d\tau]$

$=\int_{-\infty }^{\infty}f(\tau )H[\delta (t-\tau)]d\tau$

$=\int_{-\infty }^{\infty}f(\tau )h (t-\tau)d\tau$

这就是系统的零状态响应。 $r_{zs}(t)=f(t)*h(t)$

$t$ :观察响应的时刻。

$\tau$ :激励作用时刻。

某时刻的响应，是到这一时刻之前所有激励产生响应效果的加权叠加。

三.卷积的性质

1.卷积的代数运算

交换律： $\large x_{1}(t)*x_{2}(t)=x_{2}(t)*x_{1}(t)$
结合律： $\large x_{1}(t)*[x_{2}(t)*x_{3}(t)]=[x_{1}(t)*x_{2}(t)]*x_{3}(t)$

对于级联系统：

$y(t)=x(t)*h_{1}(t)*h_{2}(t)=x(t)*h(t)$

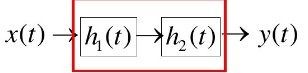
结论：（1）级联系统的单位冲激响应等于各子系统单位冲激响应的卷积；

（2）级联系统的单位冲激响应与各子系统的连接顺序无关。

分配率： $x_{1}(t)*[x_{2}(t)+x_{3}(t)]=x_{1}(t)*x_{2}(t)+x_{1}(t)*x_{3}(t)$

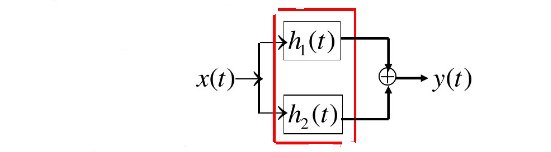
对于并联系统：

$\mathbf{y(t)=x(t)*h_1(t)+x(t)*h_{2}(t)=x(t)*[h_1(t)+h_{2}(t)]=x(t)*h(t)}$

结论：并联系统的单位冲击响应等于各子系统的和。

2.卷积的微积分性质

对于任意函数 $x(t)$ ，用 $x^{(1) }(t)$ 表示其一阶导数，用 $x^{(n) }(t)$ 表示其 $n$ 阶导数，用 $x^{(-1) }(t)$ 表示其一次积分，用 $x^{(-m) }(t)$ 表示其 $m$ 次积分。

微分性质：

若 $x(t)=x_1(t)*x_2(t)$ ， $x^{(1) }(t)=x_1^{(1) }(t)*x_2(t)=x_1(t)*x_2^{(1) }(t)$

推广到一般： $x^{(n) }(t)=x_1^{(n) }(t)*x_2(t)=x_1(t)*x_2^{(n) }(t)$

积分性质：

若 $x(t)=x_1(t)*x_2(t)$ ， $x^{(-1) }(t)=x_1^{(-1) }(t)*x_2(t)=x_1(t)*x_2^{(-1) }(t)$

推广到一般： $x^{(-n) }(t)=x_1^{(-n) }(t)*x_2(t)=x_1(t)*x_2^{(-n) }(t)$

3.与冲激函数或阶跃函数的卷积

$f(t)*\delta (t)=\delta(t)*f(t)=f(t)$

$f(t)*\delta (t-t_{0})=f(t-t_{0})$

$f(t)*{\delta }' (t)={ f }'(t)*{\delta } (t)=f'(t)$

$f(t)*{\delta }^{(n)}(t)={ f }^{(n)}(t)*{\delta } (t)={ f }^{(n)}(t)$

$f(t)*{\delta }' (t)={ f }'(t)*{\delta } (t)=f'(t)$

$f(t)*\varepsilon (t)=\int^ {t}_{-\infty}f(\tau )d\tau$

$\varepsilon (t)*\varepsilon (t)=t\varepsilon (t)$

4.卷积的时移特性

若 $f(t)=f_1(t)*f_2(t)$ ， $f_1(t-t_1)*f_2(t-t_2)=f_1(t-t_1-t_2)*f_2(t)$

$=f_1(t)*f_2(t-t_1-t_2)$

$=f(t-t_1-t_2)$

$\varepsilon (t)*\varepsilon (t-2)=(t-2)\varepsilon (t-2)$

5.时限信号的卷积

若信号 $f_1(t):t\in (t_1,t_2)$ ， $f_2(t):t\in (t_1^{'},t_2^{'})$ ，则： $y(t)=f_1(t)*f_2(t):t\in (t_1+t_1^{'},t_2+t_2^{'})$ 。

四.计算卷积的方法

1.用图解法计算卷积

两个有限长函数卷积的定义域， $(l_{1},m_{1})$ ， $(l_{2},m_{2})$ 。 $-\infty ,(l_{1}+l_{2}),(l_{1}+m_{2}),(l_{2}+m_{1}),(m_{1}+m_{2}),\infty$

应用：

第一步：将两函数的时限值两两相加，得出定义域。

第二步：确定积分限。

2.利用性质计算卷积

3.用函数式计算卷积（分段时限、卷积积分限）

4.数值解法

五.离散卷积

1.离散卷积的引入

任意序列 $x(n)$ 可表示为 $\delta (n)$ 的加权位移之线性组合：

$x(n)=...x(-1)\delta (n+1)+x(0)\delta (n)+x(1)\delta (n-1)+...+x(m)\delta (n-m)+...$

$=\sum_{-\infty }^{\infty}x(m)\delta (n-m)$

类似于： $f(t)*\delta (t)=\delta(t)*f(t)=f(t)$

对于零状态的离散线性时不变系统，若：

就必有：

时不变： $\delta (n-m)\rightarrow h (n-m)$
均匀性： $x(m)\delta (n-m)\rightarrow x(m)h (n-m)$
可加性： $x(n)=\sum_{m=-\infty }^{\infty}x(m)\delta (n-m)$
则输出： $y(n)=\sum_{m=-\infty }^{\infty}x(m)h (n-m)$

系统对 $x(n)$ 的响应 $y(n)$ =每一样值产生的响应之和，在各处由 $x(m)$ 加权。

2.离散卷积的计算

$x(n)*h(n)=\sum_{m}^{\infty }x(m)*h(n-m)$ ，m的范围由 $x(n),h(n)$ 范围共同决定。

y(n)的序列元素个数：

若 $x(n)$ 的序列长度为 $n_{1}$ ，若 $h(n)$ 的序列长度为 $n_{2}$ ，则 $y(n)$ 的序列长度为 $n_{1}+n_{2}-1$ 。

几种常用求卷积的方法

（1）解析式法

（2）图解法

（3）对位相乘求和法

（4）利用性质

六.卷积运算的两个效应

展宽：卷积的宽度等于被卷积函数的宽度之和。
平滑化：被卷积函数经过卷积运算，其细微结构在一定程度上被消除，函数本身的起伏振荡变得平缓圆滑。

注：本文整理网上资料，包括知乎、博客等，如有侵权立刻删除。

【十】卷积——2