原机器学习与数据挖掘第九讲：线性模型2

非线性变换

定义

通过转换函数 $\Phi$ 把在空间 $\mathcal{X}$ 下无法进行线性分割的数据转换为可以进行线性分割的 $\mathcal{Z}$ 空间的过程（理论上任何非线性可分数据均可转换为更高阶的线性可分的空间）。
$\mathbf{x}=\left(x_{0}, \ldots, x_{d}\right) \rightarrow \Phi \rightarrow \mathbf{z}=\left(z_{0}, \ldots \dots, z_{\tilde{d}}\right)$
其中 $d<\tilde{d}$ , $d_{v c}=d+1$ , $\tilde{d}_{v c} \leq \tilde{d}+1$ . 由于 $\mathrm{z}_i=\Phi_i (\mathrm{x})$ ， $\mathcal{Z}$ 空间是通过空间 $\mathcal{X}$ 变换而来的，在此受限情况下，可能出现小于号。
非线性变换增加了参数数量，需要更多的数据进行训练；虽然从理论上可以处理高维数据，但其泛化能力受限。

非线性变换的代价

目标：找到能够反映样本外部数据的模型，即模型泛化能力很重要，要尽量减小已有数据的影响。
Data Snooping：如果模型选择受到已有数据影响，则会削弱其泛化能力。

对于线性基本可分的数据，倘若进行非线性变化，可能产生过拟合，削弱模型泛化作用。倘若采用简单的线性可分模型，则须接受由此带来的 $E_{i n}>0$ 误差。
对在当前空间中无法线性可分或者难以进行线性分割的条件下可进行非线性转换。

Logistic Regression

在线性分类中，模型为 $h(\mathrm{x})=sign(\boldsymbol{w^T}\mathrm{x})$ ,则 $h(\mathrm{x})$ 取值为 $±1$ .
Logistic分类回归中，模型为 $h(\mathrm{x})=\theta(\mathrm{s})=\frac{e^s}{e^s+1}=\frac{1}{e^{-s}+1}$
其中 $\mathrm{s=\boldsymbol{w^T}\mathrm{x}}$ ， $\theta(\mathrm{-s})=1-\theta(\mathrm{s})$ ,且 $0<\theta(\mathrm{s})<1$ .

$\theta(\mathrm{s})=\frac{1}{e^{-s}+1}$ 被称为sigmoid函数。如下图，Logistic Regression算法将线性函数的结果映射到sigmoid函数中。

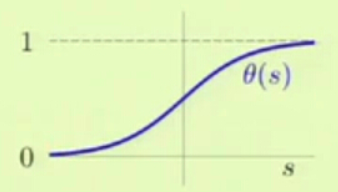
模型特点

1.logistic回归只能解决线性问题，但引入soft threshold，相对于linear regression,将结果归一化至(0,1). 可将模型值解释为概率值， $h(\mathrm{x})\rightarrow {0}$ 时，表示预测结果接近-1类，， $h(\mathrm{x})\rightarrow {1}$ 时，表示预测结果接近+1类。
2. 模型提供发生的可能性，相对于二分类确切结果，提供信息更多。

构造代价函数

构造概率模型
$P(y|\mathrm{x} )=\left\{\begin{array}{cc}{f(\mathrm{x})} & {\text { if } y=+1} \\ {1-f(\mathrm{x})} & {\text { if } y=-1}\end{array}\right.$
$f(\mathrm{x})$ 为目标函数， $P(y |\mathrm{x} )$ 为在 $\mathrm{X}$ 条件下 $y$ 发生的概率
采用 $h(\mathrm{x})$ 来近似 $f(\mathrm{x})$ ，
$P(y|\mathrm{x} )=\left\{\begin{array}{cc}{h(\mathrm{x})} & {\text { if } y=+1} \\ {1-h(\mathrm{x})} & {\text { if } y=-1}\end{array}\right.$
由 $h(\mathrm{x})=\theta(\mathrm{s})$ 及 $\theta(\mathrm{-s})=1-\theta(\mathrm{s})$ 可将上式简化：
$P(y|\mathrm{x} )=\theta(y\boldsymbol{w^T}\mathrm{x})$
极大似然估计
$\prod_{n=1}^{N} P\left(y_{(n)} | \mathrm{x}_{(n)}\right)=\prod_{n=1}^{N} \theta\left(y_{(n)} \boldsymbol{w^T}\mathrm{x}_{n}\right)$
（1）取对数似然可得

Maximize
$\mathrm{ln}(\prod_{n=1}^{N} \theta\left(y_{(n)} \boldsymbol{w^T}\mathrm{x}_{n}\right))$
即Minimize
$-\mathrm{ln}(\prod_{n=1}^{N} \theta\left(y_{(n)} \boldsymbol{w^T}\mathrm{x}_{n}\right)\\=\sum_{n=1}^{N}\mathrm{ln}(\frac {1} {\theta\left(y_{(n)} \boldsymbol{w^T}\mathrm{x}_{n}\right)})$

Cross-Entropy error(交叉熵误差度量）

将 $\theta(\mathrm{s})=\frac{1}{e^{-s}+1}$ 代入可得
$E_{in}( \boldsymbol{w})=\frac{1}{N}\sum_{n=1}^{N}\mathrm{ln}(1+e^{-y_{(n)} \boldsymbol{w^T}\mathrm{x}_{n}})$

梯度下降求 $E_{in}( \boldsymbol{w})$ 最小值

推导过程：

其中 $w(0)$ 为初始值， $\eta$ 为移动步长， $\hat{v}$ 为移动方向。

算法描述：

终止算法方法：

1、直到找到最好的 W，效果最好，但是无法确定什么时候会终止（有可能无限…）

2、设定一个阀值，当 $E_{in}$ 小于该阀值的时候终止。

3、限定迭代次数，当 t 大于某个值的时候终止。

利用该方法每次只能找到局部最优值而非全局最优值，不过我们可以通过做多次试验，每次指定不同的初始值，然后取所有结果最小的作为输出。

Reference

机器学习与数据挖掘_线性模型 II
机器学习–Logistic回归计算过程的推导