题目描述:
在与联盟的战斗中屡战屡败后,帝国撤退到了最后一个据点。依靠其强大的防御系统,帝国击退了联盟的六波猛烈进攻。
经过几天的苦思冥想,联盟将军亚瑟终于注意到帝国防御系统唯一的弱点就是能源供应。该系统由N个核电站供应能源,其中任何一个被摧毁都会使防御系统失效。将军派出了N个特工进入据点之中,打算对能源站展开一次突袭。不幸的是,由于受到了帝国空军的袭击,他们未能降落在预期位置。作为一名经验丰富的将军,亚瑟很快意识到他需要重新安排突袭计划。他现在最想知道的事情就是哪个特工距离其中任意一个发电站的距离最短。你能帮他算出来这最短的距离是多少吗?
输入格式
输入中包含多组测试用例。第一行输入整数T,代表测试用例的数量。对于每个测试用例,第一行输入整数N。接下来N行,每行输入两个整数X和Y,代表每个核电站的位置的X,Y坐标。在接下来N行,每行输入两个整数X和Y,代表每名特工的位置的X,Y坐标。
输出格式
每个测试用例,输出一个最短距离值,结果保留三位小数。每个输出结果占一行。
数据范围
1≤N≤100000,0≤X,Y≤1000000000
输入样例:
2
4
0 0
0 1
1 0
1 1
2 2
2 3
3 2
3 3
4
0 0
0 0
0 0
0 0
0 0
0 0
0 0
0 0
输出样例:
1.414
0.000
分析:
本题属于最近点对问题的变形,最近点对问题属于分治算法的经典应用。
最近点对问题,通俗的话来描述就是给我们n个点的坐标,求出其中相距最近的两个点的距离。显然,暴力做法是依次枚举两点,找出最小距离,复杂度为平方级别。像本题十万的数据级别,平方一下就是10位数,大概需要100s,是我们所不能接受的。于是采用分治法来优化时间复杂度到O(nlogn)。

随便盗张图,然后讲下思路。分治首先要将原问题一分为二,将n个点分成两组大致相等的点,于是一般根据这些点的横坐标进行排序,从而从中间将这些点分成了左右两部分。根据分治的一般思路,递归的求解两个子问题然后合并子问题的解。递归的求解左右两个部分的点是没有问题的,但是在合并子问题的解时,设δ = min(左边点的最小距离,右边点的最小距离),我们所求的最近距离并不是就等于δ的。可能存在一个点在左边,另一个点在右边,它们的距离是小于δ的。而且可能影响到解的点只可能在距离分界线不超过δ的区域(如上图所示)。对于该区域上的任意一点,以它为圆心做半径为δ的半圆的区域内的点才可能影响到解,考虑到极端情况,即分割线上的一点,向右做半径为δ的半圆,如下面左图所示,超过了半圆区域的右边区域的点都不可能影响到最小距离,为了方便,将半圆扩张成一个长为2δ,宽为δ的矩形。要知道在此之前,δ以及是左边和右边点的最短距离了,所以在该矩形区域中至多能存在6个点,也就是下面左边的图所标注的六个点。下面简单证明下最多只有六个点,如下面右图所示,将该矩形分成六个大小相等的区域,长为2/3δ,宽为1/2δ,对角线长为5/6δ,显然在任意一个小矩形中不可能存在两个点,若存在则其距离会小于δ。知道了在距离分割线δ的区域内的任意一点,在其右边至多有六个点可能影响解,最坏情况下也就是6n的复杂度,意味着我们在合并子问题时只需要对距离分割线δ内的带状区域中每个点遍历一个矩形区域即可。
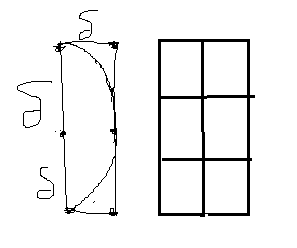
如何处理本题?只需将点的类别做个区分,当两个点的类型相同时将他们之间的距离置为无穷大即可。此外,在合并子问题解的时候需要注意,如果找到带状区域内的所有点后对它们再次排序,以方便找到矩形区域内的点,那么整体的时间复杂度将是nlognlogn级别的,倘若在合并的同时对合并的点按y进行排序,那么将在线性的时间内完成排序,整体复杂度是nlogn。
至于为什么要对带状区域的点排序,试想一下,如果不排序,假设所有的点都在该区域内,暴力的求解分割线两边点的距离,最后的复杂度还是平方级别。而上面所分析的,对于每个点只需要考察矩形内的点,显然每个矩形内的点纵坐标是单调的,所以排序后就不用遍历所有的点而只需遍历相邻的几个点即可。
#include <iostream>
#include <cmath>
#include <algorithm>
using namespace std;
const int maxn = 200010;
const double INF = 10e9;
double res = INF;
struct Point{
double x,y;
bool type;
bool operator< (const Point &W) const{
return x < W.x;
}
}points[maxn],temp[maxn];
double dist(Point a,Point b){
if(a.type == b.type) return INF;
double dx = a.x - b.x,dy = a.y - b.y;
return sqrt(dx * dx + dy * dy);
}
double dfs(int l,int r){
if(l >= r) return INF;
int mid = l + r >> 1;
double mid_x = points[mid].x;
double ans = min(dfs(l,mid),dfs(mid + 1,r));
res = min(res,ans);
{
int k = 0,i = l,j = mid + 1;
while(i <= mid && j <= r){
if(points[i].y <= points[j].y) temp[k++] = points[i++];
else temp[k++] = points[j++];
}
while(i <= mid) temp[k++] = points[i++];
while(j <= r) temp[k++] = points[j++];
for(int i = 0,j = l;i < k;i++,j++) points[j] = temp[i];
}
int k = 0;
for(int i = l;i <= r;i++){
if(points[i].x >= mid_x - res && points[i].x <= mid_x + res) temp[k++] = points[i];
}
for(int i = 0;i < k;i++)
for(int j = i - 1;j >= 0 && temp[i].y - temp[j].y <= res;j--)
res = min(res,dist(temp[i],temp[j]));
return res;
}
int main(){
int T,n;
cin>>T;
while(T--){
cin>>n;
for(int i = 0;i < n;i++){
cin>>points[i].x>>points[i].y;
points[i].type = 0;
}
for(int i = n;i < 2 * n;i++){
cin>>points[i].x>>points[i].y;
points[i].type = 1;
}
sort(points,points + 2 * n);
printf("%.3f\n",dfs(0,2 * n - 1));
}
return 0;
}