Methods for Non-Linear Least Squares Problems 非线性最小二乘问题的方法
2nd Edition, April 2004
K. Madsen, H.B. Nielsen, O. Tingleff
1 Introduction and Definitions
第一章 介绍和定义
这本小册子主要关注 Least Squares Problem

最小二乘问题是全局最优化问题的一个特例,全局最优化问题:

这个问题很难,一般情况下我们寻找 F 的一个局部极小解
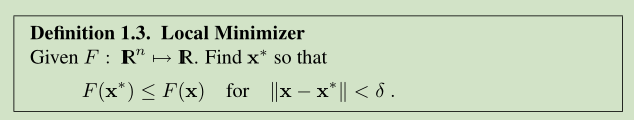
这里我们假定 cost function F 是 differentiable 以及足够平滑,其泰勒展开如下:

如果 x* 是一个局部极小值,||h|| 足够的小,那么我们就不能找到一个点 x*+h 使其对应的 F 值更小,我们根据这个 observation 并结合 (1.4a) 得到如下结论:

所以一个局部极小解的点 同时也是一个 stationary point,但是局部极大值点也是一个 stationary point。如果一个 stationary point 既不是局部极大值也不是局部极小值点,它就称之为 saddle point,为了确定一个给定的 stationary point 是不是一个局部极小值点,我们需要在泰勒展开中包含二阶项。

注意: 根据 stationary point 的定义, 上面的一阶项为 0,所以泰勒展开就没有了一阶项。
根据 Hessian 的定义,我们知道任意的 H 是一个 对称矩阵,如果我们要求 Hs 是 正定 positive definite,那么其对应的所有特征值大于一个数 δ >0
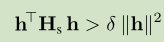
所以如果 ||h|| 足够小,(1.7)式右边的第三项受二阶主导,而二阶项始终为 正,所以我们的得到

假定 xs 是一个 stationary point, F”(xs)是正定,那么 xs 是一个极小值点。如果 Hs 是负定,那么 xs 是一个局部极大值点。 如果 Hs 是 indefinite(同时具有正负特征值),xs 是一个 saddle point
111