数据挖掘（简单分析）

处理“单连续变量”

缺失值：df.isnull()　　#df就是加载进来的数据，DataFrame类型的
异常值:　箱型图模型

画图：

核密度估计：sns.kdeplot()
直方图图： sns.distplot()

判断方法：df.info()

分类：连续型（continuous）和标称型或分类变量（categorical）

 f= r'movies_metadata.csv'
 df =pd.read_csv(f)  #加载数据  df是DataFrame类型
 print(df.info())    #输出数据信息（数目、类型）

输出结果:

在这里插入图片描述

分析统计数据：df.describe()

f= r'movies_metadata.csv'
df =pd.read_csv(f)  #加载数据  df是DataFrame类型
print(df.describe())    #输出统计信息

输出结果：

在这里插入图片描述

d = df['P10'] #可以通过这个来取出某列得数据

进阶版：

https://www.kesci.com/home/project/59f687e1c5f3f511952baca0

#In 1
import numpy as np
import pandas as pd
from scipy import stats, integrate
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline

#In 2
import seaborn as sns
sns.set(color_codes=True)

In 3
np.random.seed(sum(map(ord, "distributions")))

Hist

一般对于单变量,我们最喜欢的就是直接绘制出大致的直方图.而最简单的方法就是采用hist方法(注意该方法是在matplotlib.pyplot中,下面我们介绍的可视化工具主要都会基于seaborn库),该方法可以直观地让我们了解到散落在各个区间的数据的情况(数据分布),hist默认为10个bins.

x = np.random.normal(size=100)
plt.hist(x)

在这里插入图片描述

Kdeplot

对于连续的变量,光看直方图肯定是不够的,数据的分布的观察也是必不可少的,这时我们需要借用KDE(Kernel Density Estimate)函数.

sns.kdeplot(x,shade=True)

在这里插入图片描述
Distplot

上面的两个函数非常实用,但是还有一个非常好的函数,distplot函数,该函数包含了绝大多数单变量可视化的能力,可以直接使用distplot实现上面两个函数的功能,此外它还可以绘制出其他的近似分布.
默认的distplot能直接绘制出我们需要的直方图以及对应的核密度估计(KDE).

扫描二维码关注公众号，回复： 5968532 查看本文章

sns.distplot(x);

在这里插入图片描述
当然如果不想看到kde曲线,我们可以直接将kde去掉,如果只想看kde曲线,我们也可以把直方图去掉.

sns.distplot(x, kde=False, rug=True);

在这里插入图片描述
当然也可以将直方图省去.仅看kde曲线.

此外还有一个神奇的操作–设置bin的个数,它会生成对应的bin来告诉你数据的一个分布的情况,大致分布在每个bin中的数据有多少,经常可以看到有些人喜欢通过观察bin来对数据进行切分并做one-hot编码形成新的特征[4] .

sns.distplot(x, bins=20, kde=False, rug=True);

连续(continious)的二元变量特征的数据可视化

上面的数据可视化是基于单变量的,常常用于对连续形式的label(回归问题中较为常见)进行观察处理,实际问题中我们不会仅仅只对数据进行观察,还需要进行预测等,自然而然的,数据之间关系的分析就显得非常重要.此处我们开始对数据之间的关系进行分析,主要是两个连续变量之间的相关性分析.关于涉及categorical变量的部分我们会在第后续分进行介绍.

标准高斯函数

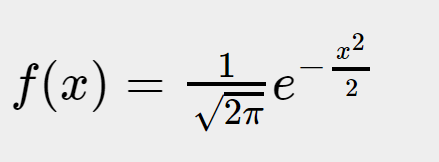
在这里插入图片描述
高斯函数标准型：

在这里插入图片描述
这个函数描述了变量 x 的一种分布特性，变量x的分布有如下特点：
Ⅰ，均值 = 0
Ⅱ，方差为1
Ⅲ，概率密度和为1

一元高斯函数一般形式

在这里插入图片描述
一元高斯函数一般形式：

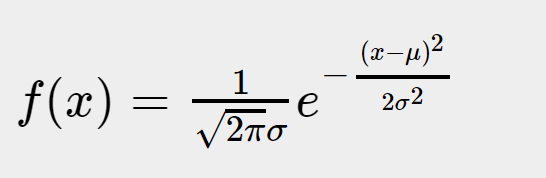
我们可以令：

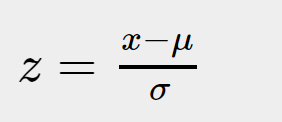
称这个过程为标准化，不难理解，z∼N(0,1)，从z -> x的过程如下：
Ⅰ，将 x 向右移动 μ 个单位
Ⅱ，将密度函数伸展 σ 倍
而标准化(x -> z)所做的事情就是上述步骤的逆向
唯一不太好理解的是前面 12π√σ 中的σ，为什么这里多了一个 σ，不是 2σ 或其他？
当然，这里可以拿着概率密度函数的性质，使用微积分进行积分，为了保证最终的积分等于1，这里必须是 σ
这里我想说一下自己的直观感受：
在这里插入图片描述
实线代表的函数是标准高斯函数：

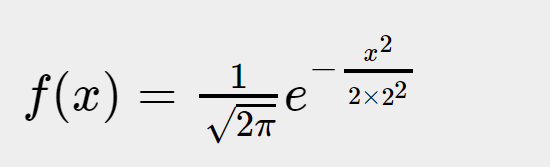
虚线代表的是标准高斯函数在 x 轴方向2倍延展，效果如下：
A(x = 1) -> D(x = 2)
E(x = 1.5) -> F(x = 3)
G(x = 2) -> H(x = 4)
横向拓宽了，纵向还是保持不变，可以想象，最后的函数积分肯定不等于1
采用极限的思想，将 x 轴切分成无穷个细小的片段，每个片段可以与函数围城一个区域，因为我的切分足够小，这个区域的面积可以近似采用公式：面积 = 底 × 高求得：
从 AQRS -> DTUV，底乘以2倍，高维持不变，所以，要保持变化前后面积不变，函数的高度应该变为原来的 1/2
所以高斯函数在 x 轴方向做2倍延展的同时，纵向应该压缩为原来的一半，才能重新形成新的高斯分布函数
扩展到一般情形，x 轴方向做 σ 倍延拓的同时， y 轴应该压缩 σ 倍（乘以 1/σ）
更多请看：
https://www.cnblogs.com/bingjianing/p/9117330.html
用多元高斯分布函数生成两个变量x,y.

mean, cov = [0, 1], [(1, .5), (.5, 1)]
data = np.random.multivariate_normal(mean, cov, 200)
df = pd.DataFrame(data, columns=["x", "y"])

df.head()

Scatterplot

这个函数是通用的,尤其是两个变量都是连续型变量的时候,我们希望看看在二维平面上二者之间的关系时必然会先想到散点图函数,当然当数据比较多的时候,建议采样观察,不然真的很耗时.通过Scatterplot我们可以很容易的发现一些数据的分布规律,是否有簇的存在等等,在涉及类似于经纬度的问题时,我们经常会通过scatterplot看数据,然后考虑聚类等操作.

plt.scatter(df['x'].values,df['y'].values)

在这里插入图片描述
Jointplot

Scatterplot函数是非常实用的,但是用过seaborn的伙伴肯定都还会知道joinplot这个函数,不仅能方便的绘制散点图,同时还融入了很多其他功能,还可以帮我们直接进行一些简单的模型的拟合(linear regression,etc).

sns.jointplot(x="x", y="y", data=df);

在这里插入图片描述