1、关联式容器
前面刚开始整理 STL 容器 时，简单的说了一下容器可以分为两类 序列式容器 和 关联式容器。前面又对主要的 序列式容器 进行了整理，今天终于轮到 关联式容器了。
所谓关联式容器，观念上类似关联式数据库：每笔数据都有一个键值（key）和一个实值（value）。当元素插入到关联式容器中时，容器内部结构便依照其键值大小，以某种特定规则将这个元素放置于适当位置。关联式容器没有所谓头尾（只有最大元素和最小元素），所以不会有所谓 push_back()、push_front()、pop_back()、pop_front()、begin()、end()等操作。
标准的 STL 关联式容器分为 set（集合） 和 map （映射）两大类，以及这两大类的衍生体 multiset（多重集合）和 multimap（多重映射表）。这些容器的底层机制均以 RB-tree （红黑树）完成。RB-tree 也是一个独立容器，但并不开放给外界使用。
此外，还有一些 STL 库提供了一个不再标准规格之列的关联式容器，如hash table，以及以此衍生出的 hash_set、hash_map、hash_multiset、hash_multimap等。
2、树的导览
一般而言，关联式容器的内部结构是一个 balanced binary tree（平衡二叉树），以便获得良好的搜寻效率。balanced binary tree 有许多种类型，包括 AVL-tree、RB-tree、AA-tree，其中最被广泛运用于STL的是 RB-tree（红黑树）。为了探讨 STL 的关联式容器，我们必须先探讨RB-tree。而要探讨 RB-tree，我们需要先来探讨树。
树（tree），在计算机科学里，是一种十分基础的数据结构。几乎所有操作系统都将文件存放在树状结构中，几乎所有的编译器都需要实现衣蛾表达式树；文件压缩所用的哈夫曼算法需要用到树状结构；数据库所使用的 B-tree 则是一种相当复杂的树状结构。
对于树的术语，我在 数据结构第六篇 中有整理。大家感兴趣可以回看一下。
2.1、二叉搜索树（binary search tree）
所谓二叉树搜索树，可提供对数时间的元素插入和访问。二叉搜索树的节点放置规则是：任何节点的键值一定大于其左子树中的每一个节点的键值，并小于其右子树中的每一个节点的键值。因此，从根节点一直往左走，直至无左路可走，即得最小元素；从根节点一直往右走，直至无路可走，即得最大元素。
要在一棵二叉搜索树中找出最大元素或最小元素，是一件极简单的事。比较麻烦的是元素的插入和移除。
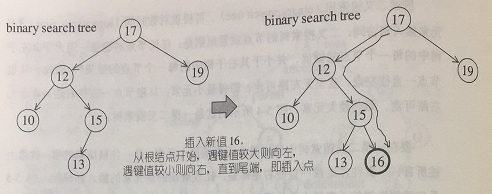
插入操作：从根节点开始，遇键值较大者就向左，遇键值较小者就向右，一直到尾端，即为插入点。如下图所示：
移除操作分为两种情况：
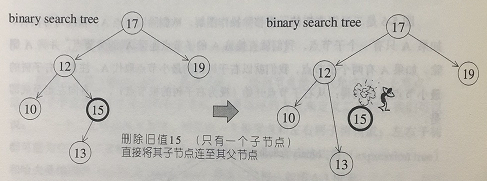
1、如果 A 只有一个子节点，我们就直接将 A 的子节点连至 A 的父节点，并将 A 删除。如下图：
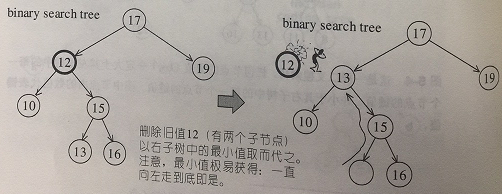
2、如果 A 有两个子节点，我们就以右子树内的最小节点取代 A。注意，右子树的最小节点极易获得，从右子节点开始，一直向左走至底即是。如下图所示：
2.2、平衡二叉搜索树（balanced binary search tree）
有时因为输入值不够随机，有时因为经过某些插入或删除操作，二叉搜索树可能会失去平衡，造成搜索效率低落的情况，如下图所示：
所谓树形平衡与否，并没有一个绝对的测量标准。“平衡”的大致意义是：没有任何一个节点过深。不同的平衡条件，早就出不同的效率表现，以及不同的实现复杂度。有数种特殊结构如 AVL-tree、RB-tree、AA-tree，均可实现出平很二叉搜索树，它们都比一般的二叉搜索树复杂，因此，插入节点和删除节点的平均时间也比较长，但是它们可以避免极难应付的最坏情况，而且由于它们总是保持某种程度的平衡，所以元素的访问时间平均而言也就比较少。一般而言其搜寻时间可节省25%左右。
2.3、AVL tree（adelson-velskii-landis tree）
AVL tree 是一个 “加上了额外平衡条件” 的二叉搜索树。其平衡条件的建立是为了确保整棵树的深度为 O(logN)。直观上的最佳平衡条件是每个节点的左右子树有着相同的高度，但我们很难插入新元素而又保持 这样的平衡条件。AVL tree 于是退而求其次，要求任何节点的左右子树高度相差最多 1。
下图所示的是一个AVL tree，插入了节点 11 之后，灰色节点违反 AVL tree 的平衡条件。由于只有 “插入点至根节点” 路径上的各节点可能改变平衡状态，因此，只要调整其中最深的那个节点，便可使整棵树重新获得平衡。
前面说过，只要调整 “插入点至根节点” 路径上，平衡状态被破坏之各节点中最深的那一个，便可使整棵树重新获得平衡。假设该最深节点为 X，由于节点最多拥有两个子节点，而所谓 “平衡被破坏” 意味着 X 的左右两颗子树的高度相差 2，因此我们可以轻易将情况分为四种：
1、插入点位于 X 的左子节点的左子树----左左
2、插入点位于 X 的左子节点的右子树----左右
3、插入点位于 X 的右子节点的左子树----右左
4、插入点位于 X 的右子节点的右子树----右右
情况1、4彼此对称，称为外侧插入，可以采用单旋转操作调整解决。情况2、3彼此对称，称为内侧插入，可以采用双旋转操作调整解决。
2.3.1、单旋转（Single Rotation）
在外侧插入状态中，k2 “插入前平衡，插入后不平衡” 的唯一情况如图左侧所示。A 子树成长了一层，致使它比 C 子树的深度多 2。B 子树不可能和 A 子树位于同一层，否则 k2 在插入前就处于不平衡状态了。 B子树也不可能和 C 子树位于同一层，否则第一个违反平衡条件的将是k1 而不是 k2。
为了调整平衡状态，我们希望将 A 子树提高一层，并将 C 子树下降一层，调整之后如上图右侧的图形。我们可以这么想象，把k1 向上提起，使 k2 自然下滑，并将 B 子树挂到 k2 的左侧。这么做是因为，二叉搜索树的规则使我们知道， k2 > k1，所以 k2 必须成为新树形中的 k1 的右子节点。二叉搜索树的规则也告诉我们， B子树的所有节点的键值都在 k1 和 k2 之间，所以新树形中的 B 子树必须落在 k2 的左侧。
以上所有的调整操作只需要将指针稍作修改就可迅速达成。
2.3.2、双旋转（Double Rotation）
对于内侧插入造成的不平衡状态，单旋转无法解决这种情况，如下图所示：
这种情况下，可以通过两次单旋转来满足 AVL-tree的平衡条件，所以叫双旋转。具体的操作是在 k1 和 k2 之间做一次单旋转，然后在 k2 和 k3 之间在做一次单旋转，如下图所示：
因为RB-tree 也用到了 单旋转 和 双旋转，代码会在 RB-tree 中进行整理，感兴趣的可以前往查看。
感谢大家，我是假装很努力的YoungYangD（小羊）。
参考资料：
《STL源码剖析》