6.1 对偶表示（PRML读书笔记）

本节小结

  许多回归的线性模型和分类的线性模型的公式都可以使⽤对偶表⽰，从而引出了核函数。本小节将正则化的平方误差函数（公式6.2）转换成对偶表示（公式6.9）。


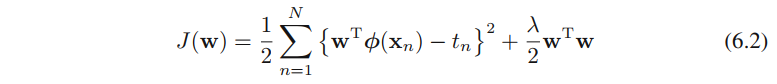
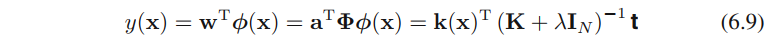
其中，
   $\textbf{k}(\textbf{x})^T=(k(\textbf{x}_1, \textbf{x}),...,k(\textbf{x}_N,\textbf{x}))$（N为样本数目）
  K是⼀个N × N的对称矩阵，元素为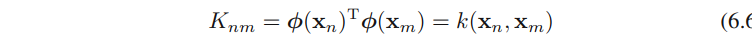
其中

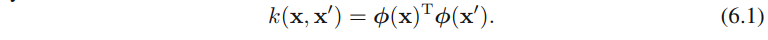
  由公式6.9可得，因此我们看到对偶公式使得最⼩平⽅问题的解完全通过核函数 $k(\textbf{x},\textbf{x}^{'})$表⽰。我们可以直接针对核函数进⾏计算，避免了显式地引⼊特征向量 $\phi(\textbf{x})$，这使得我们可以隐式地使⽤⾼维特征空间，甚⾄⽆限维特征空间。

  关于对偶表示及核函数的实际意义，有待继续阅读后续章节。

待解决问题

• “对偶表示推导”的再理解，如何证明公式6.2和公式6.9的最小值一样，为什么采用这样的对偶表示方式
• 公式6.9中的 $\textbf{K}+\lambda\textbf{I}_N$为什么一定可逆
• 根据公式6.9， $\textbf{a}$的解可以被表⽰为 $\phi(\textbf{x})$的线性组合，从⽽我们可以使⽤参数向量w恢复出原始的公式（这一句需要再理解）。
• 基于Gram矩阵的对偶表⽰的存在是许多线性模型的性质，包括感知器。在6.4节，我们会研究回归的概率线性模型和⾼斯过程⽅法的对偶性。当我们在第7章讨论⽀持向量机的时候，对偶性也起着重要的作⽤（看完后续章节之后回看）。