The Lovasz Hinge: A Novel Convex Surrogate for Submodular Losses

看完本文感觉比 上篇论文清晰一些了，但是也只是懂了一点，还需要多看几遍吧。

1.介绍

统计学习在很大程度将问题定位在损失函数在个体样本上的分解。然而，在许多情况下，非模块化损失必须被最小化。这种情况下，当预测系统的多个输出被当做决策过程的基础，从而产生一个单一的现实结果。因此，预测效果的这些依赖性(而不是预测本身之间的统计依赖性)通过非模块的损失函数融入到学习系统。本文中，我们的目的是提供一种新的学习算法的理论基础和算法基础来使子模块损失的学习算法可行，一个重要的子模块的非模块损失在现有算法中不可行。本文对我们的会议论文进行了统一和扩展的介绍。
凸代理损失函数是经验风险最小化的实际应用的核心。二元分类和回归的凸代理的设计中，已经开发出了简单的规则，在结构化输出的设置中，边界和松弛缩放是定义更一般输出空间的凸代理的两个原则，尽管边界和松弛调整在约束任意损失函数具有明显的灵活性，在实践中应用这些方法存在着根本的限制：

• 它们为某些损失函数提供宽松的上界
• 计算梯度或切割平面对于子模块损失函数来说是NP难题
• 一致性结果通常是缺乏的

在实践中，尽管非模块损失(Jaccard loss)已经被应用到结构化预测的设置中，但模块化损失(如Hamming loss)通常被应用来保持可牵引性。在本文中表明，Jaccard loss事实是一个子模损失，我们提出的凸代理提供了一个多项式时间的紧的上界。
在多分类问题背景下已经考虑过非模块的损失。使用模块化的Hamming loss和0-1子集损失以及超模块的秩损失；当使用一个基于F-score的非子模的损失，引入子模pairwise potentials，而不是子模损失函数。使用加权模块化的Hamming loss，但也提出了一个新的基于树的训练算法；使用子模块损失，Hamming loss和非模块化的F1 loss。如果测试时的相关损失是非模块化的，那么必须优化训练时的正确损失。然而，非超模损失函数在文献中更为罕见。
这项工作中，我们基于集合函数Lovasz扩展，介绍了一种子模块损失的替代原则来构建凸代理损失函数。子模块函数的Lovasz扩展是它的凸闭包，并已经应用到其他的机器学习上下文中。通过寻找代理函数是集函数扩展的充分必要条件，我们分析了边界和松弛重缩放是紧凸代理的设置。虽然边界和松弛重定会产生一些子模集合函数的扩展，但他们的优化是NP难题。因此，我们提出了一种新的基于Lovasz扩展的子模函数凸代理，称之为Lovasz hinge。相比于边缘和松弛重定，Lovasz hinge为所有子模损失函数提供了一个紧的凸代理，并且梯度的计算或平面切割可以在O(plogp)时间完成，同时具有一个与损失函数的线性数字的连接数。我们验证了应用Lovasz hinge切平面优化策略的经验快速收敛性，表明优化子模损失可以降低测试集的平均损耗。在第2节中，我们介绍了经验风险最小化背景下的子模损失函数的概念。结构化输出SVM是内部依赖的输出的经验风险最小化的常用对象，我们在第3节证明了它在非模块化损失函数的特性。第4节，我们介绍了Lovasz hinge以及凸性、计算复杂性。我们依靠经验证明它在合成问题上的性能，在第6节，是在Pascal VOC数据集和Microsoft Coco数据集上的图像分类和标记任务上。

2.子模块损失函数

在经验风险最小化中，我们用有限样本损失和来估计预测函数f的风险

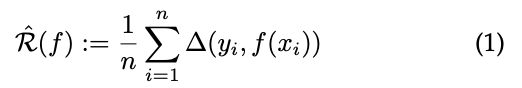
对于经验风险最小化原则的实际应用，必须用凸代理近似或限定离散损失函数∆的上界。我们将为特定损失函数确定一个凸代理，方式是将一个函数从离散域映射到连续域。特别地，我们将研究离散域是一组p二进制集合预测的情况。表示为以下公式：

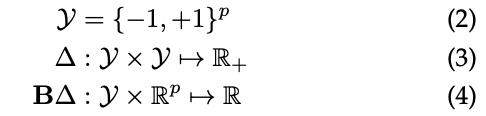
B是一个从∆构建代理损失函数的操作，我们假设

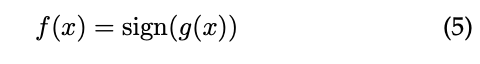
$g:X->R^p$一个参数化预测函数，通过经验风险最小化进行优化。
关键特性是b∆和∆之间的关系。特别是，我们感兴趣的是，当给定的替代策略b∆产生∆的扩展时（参见定义3）。我们通过用给定的p维单位超立方体Rp标识{−1，+1} p使这个概念正式化。我们说B∆（y,）是∆（y,）的扩展，只要函数在这个单位超立方体的顶点上相等。我们关注于函数扩展，因为它们确保了离散损失和凸代理之间的紧密关系。

2.1 集合函数和子模块

对于许多优化问题，定义在给定基础集合的集合函数通常被考虑应用到最大值最小值求解中。子模块的函数在这些集合函数扮演重要的角色，就像替换函数在变量空间的作用。
子模块功能可以通过多种相同的性质定义，我们使用下列定义

如果一个函数的负模是子模块，则它为超模块；一个函数即使子模又是超模则是模块。模函数可以写成二元向量{0,1}p的点乘，构建了一个V的子集和一个 $R^p$中的协同向量
定义2 对于所有的子集A属于V，下式是增的。
公式(9)给出了错误预测时的损失函数

关于文中词语的理解

3.存在的凸代理

这一节，我们分析两种存在的凸代理：边界重定和松弛重定。我们确定了边界和松弛重定的必要和充分条件，以得到一个底层集损失函数的扩展，并解决了它们在子梯度计算复杂度方面的缺点。
一般的问题是学习从输入x∈X 到离散输出（标签）y∈Y的映射f。结构化输出SVM（SoSVM）是规范化风险最小化常用的一种框架。SOSVM追求的方法是在输入/输出对上学习一个函数h:X×Y →R，通过最大化下式可以获得预测(其实就是最大化类别为1的概率值)。

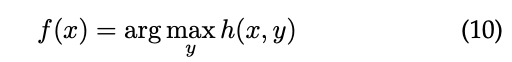
然后将h替代为再生核希尔伯特空间输入x和输出y的特征融合。

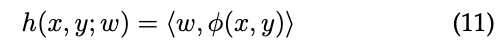
有界的损失函数 ∆：YxY→R 定义了预测值和真实值的损失，并被用来重塑边界，参数通过下式来优化。

一个分割平面的和一个松弛重定的算法如下图

接下来，我们考虑 $x_i∈X$是一个p个元素的有序集合， $y_i∈Y$是一个二元向量{-1,1}p。我们考虑的特征图如下：(终于找到你了…)

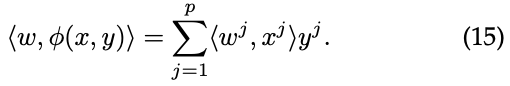
然后可以定义g并重新表示h(x,y)

本节是基于线性参数函数发展的，本文的结果代理提供了更一般的函数的有效子梯度，关于更一般函数分类的优化问题留给了后续的工作。

3.1扩展

为了分析是否操作B为 ∆产生扩展，我们通过如下定义构建了一个到p维向量空间的映射。

3.2和3.3

3.2和3.3是关于公式(21)和(22)的证明，太长，这里先不看，继续以读懂全文为目的。

3.4 子梯度的计算复杂性

边界和松弛重定的子梯度的计算如下式：

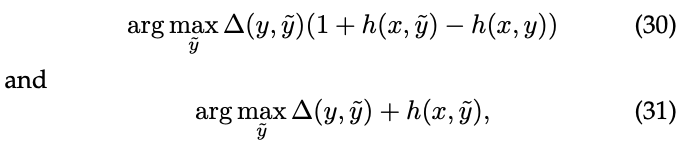
这个计算是NP难题，这样的损失函数目前的方法是不可行的，因此，我们介绍Lovasz hinge来作为替代的操作，为子模块损失构建一个可行的凸代理。

4.Lovasz Hinge

接下来基于Lovasz扩展为子模块损失函数发展凸代理，对p个元素进行了c重新排列π，使其满足 $S^{π_i}$是递减的，并定义了集合函数l

4.1 Lovasz 扩展

这部分我们介绍一个奇特的子模损失的凸代理。这个代理是基于子模集合函数相关的基础结果和分段的线性凸函数，我们称为Lovasz 扩展。他可以允许从超立方体{0,1}p的顶点到超立方体{0,1}p的全体的扩展。Lovasz扩展的定义如下。其核心是，对于任意的一个向量 $s∈[0,1]^p$，我们对它的组成以降序排序，然后定义l(s)。

与子模函数相关的有两个多面体：子模多面体和基础多面体。

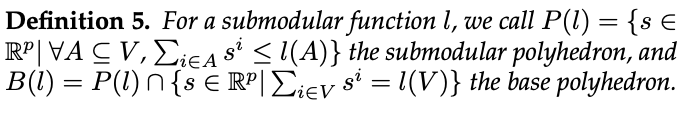
Lovasz扩展连接子模集函数和凸函数。此外，我们可以用Lovasz扩展的凸优化代替子模集函数的离散优化。算法如下：

计算 $s^Tu$的最大值与计算Lovasz扩展的子梯度步骤相同。对s的p个组成元素排序，算法复杂度O(plogp)，然后计算 $s^Tu$的值复杂度为O§。
贪心算法等同于下式：

函数l是子模函数当且仅当它的Lovasz扩展是凸的。我们可以利用这一点构建一个子模损失函数的凸代理。

4.2 Lovasz hinge

对于子模块l，我们定义Lovasz hinge L为下式

Lovasz hinge是Lovasz扩展从[0,1]p到Rp的一个扩展，当l是子模增长的，我们给s的每一个消极组成设定一个阈值(通过max(,0))，则当l增长，公式的后半部分就不会是消极的。当其他情况，我们则通过整个取max(,0)。
通过后面两个命题，我们可以得出上述定义返回的代理是凸的并且是损失函数的扩展。(证明省略)。
对于一个子模增长的损失函数l，定义6情况1中的Lovasz hinge，与SVM在Hamming损失一致。
hinge损失可以被描述为下式。

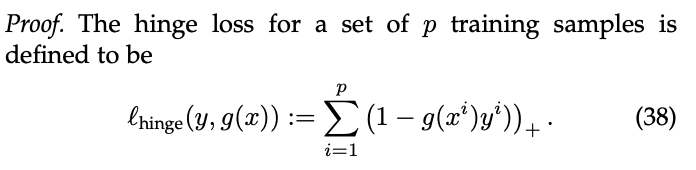
我们将定义6情况1的Lovasz hinge简化为下式

通过一个引理帮助证明Lovasz hinge在单元立方[0,1]p与边界和松弛重定相比相同或更高的价值。
边缘和松弛重定可能具有额外的反射点在Lovasz hinge没有展现，但可以证明，所有的三个分段线性扩展，在单元立方顶点上有相同的值

我们在Lovasz hinge采用不同的阈值策略，是因为，如果非单调的损失中我们对每一个s的消极组成都限定0为边界，将不能保证Lovasz hinge是总是凸的。关于这点在命题10证明，此处省略。
下图表现了一个l为非单调情况下的损失表面，我们可以看到在一个顶点的一侧下降的元素导致了一个消极的子梯度，而在另一侧子梯度为0(我们设定的阈值策略)，因而导致了非凸的表面。

4.3子梯度计算的复杂性

为了解决最大边问题，我们探索性的提出了平面切割的算法。第5行我们利用Lovasz hinge计算了经验损失的上界，第6行我们通过计算相关的排列π(而不是所有可能的输出)计算了损失梯度。

由于切平面或损失梯度的计算与计算Lovasz扩展值的步骤恰恰相同，具有相同的复杂性O(plogp)排序p个系数，然后损失函数连接的O§复杂性。这恰恰是一个贪心算法优化子模多面体上的线性规划。在我们的实现中，我们采用了一个松弛切割平面优化，我们观察到原始双间隙的经验收敛性，其速度与结构化输出SVM的速度相当。

4.4凸代理的可视化

我们考虑一个简单的二分类在两个样本的损失函数。如下图：

在上图的图3中，x代表 $s^1$,y代表 $s^2$，z则是代理损失函数，并且以实点画出了l在单位立方顶点的值。
我们发现子模增长函数的Lovasz hinge表面都是凸的。并且阈值策略一左一右添加了两个保存凸性的超平面。然后我们观察到，所有与离散损失函数值相对应的固体点接触到表面，这从经验上验证了代理是离散损失的扩展。这里我们将l设置为对称函数，而扩展也可以验证非对称递增集函数。此外，当S上的阈值策略仍在应用时，我们用非单调函数绘制了Lovasz hinge与图3（c）和图3（d）相比，由于S的负分量上的阈值策略，凸性丢失。

5.Jaccard Loss

Jaccard index score被广泛应用到评估两个样本集的相似性、不同的预测问题如图像切割等。这个部分我们介绍了基于Jaccard index score的Jaccard loss，并且证明了Jaccard loss是一个关于预测失误元素集的子模函数。

研究证明 $∆_J$是子模loss。

6.实验结果

关于实验结果这里省略了。