数字的算法--大数加法

很多算法教程里都讨论过大数乘法，对于长数字的加法却很少做分析。因为正常的数字在计算机上一条指令就完成了加法操作。但是对于超过了计算机表示位数的大数字，加法需要按位操作计算。尽管也很简单，但是有一些细节容易忽略。
对于两个n位数的加法，我们首先对齐它们的右端，然后从右至左的按位执行加法操作。在操作过程中维持一个进位，因此每个计算都可以看作三个一位数的加法操作。下面给出一个例子：

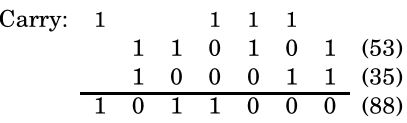
对于两个n位数相加，最终结果最多是n+1位的，这看起来不言自明，但是我在这里更加严谨的证明一下：

1. 首先每位计算都会产生一个结果，数字有n位，所以结果位数不少于n
2. 下面还有两个结论：
   （1）三个一位数的相加的进位最大为也是一位数
   （2）三个一位数相加的结果最多是两位数
   我们来证明这两条结论，假设我们进行的b进制加法，两个最大的一位数相加的结果： x = b-1+b-1+b-1
   如果b=2,x=11,进位1,结果两位数，满足（1）（2）
   如果b>=3,x=2*b+b-3,b-3保留在本位，2为进位，结果是两位数。因为进位最大是2，所以最后相加的和一定小于x（每位加法最大是b-1+b-2+2），不会超过两位。
   比如十进制表示下的三个一位数相加的最大值：9+9+9=2*10+10-3 = 27 ，进位为2，结果是两位数
   经过上面的证明我们可以得出结论是，n位数的加法结果最多是n+1位，每位的加法操作耗时 $c_1$,最后可能的n+1位耗时为 $c_0$,那么时间复杂度是 $c_0+c_1*n$,即 $O(n)$的时间复杂度。

对于这个结果，有时还是不能令人满意，因为我们通常知道输入的数字x,y的具体表示，不知道具体位数。我们需要知道b进制数字x的位数是多少？

n位b进制数据表示的最大值是 $b^n-1$,例如5位二进制的表示最大值为 $11111_2$= $2^5-1$。
n+1位b进制数据表示的最大值是 $b^{n+1}-1$
当 $b^n=<x<b^{n+1}$,位数是n+1,即 $\lfloor log_bx \rfloor$+1,使用大O表示时间复杂度大致为 $O(log_bx)$。通常用对数表示时间复杂度时，写法是 $O(logx)$,表示以2为底的对数。这是因为根据换底公式可以得到 $log_bx=log_2b*log_2x$,省略常数后，可以得到一致的表达。

对于两个加数位数不同的情况，时间复杂度以较大的那个数的位数来算，结果是一样的。下面是多位二进制加法的代码：

public String BinaryPlus(String s1, String s2) {
		int len1 = s1.length();
		int len2 = s2.length();
		int step = 0;
		List<Character> ls = new ArrayList<>();
		while(len1>0||len2>0) {
			int x = len1>0?s1.charAt(len1-1)-'0':0;
			int y = len2>0?s2.charAt(len2-1)-'0':0;
			ls.add((char) ((x+y+step)%2+'0'));
			step = (x + y + step)/2;
			len1--;
			len2--;
		}
		if(step==1)
			ls.add('1');
		Collections.reverse(ls);
		return ls.toString().replaceAll("[\\[\\], ]", "").replaceAll("^0*","");
	}