用一个浮点数相加的例子来演示计算机在计算时所产生的误差。
在Python中,用0.2+0.4 会得到0.6000000000000001。
浮点数简介
浮点数的表示方法:目前流行的浮点数标准是IEEE754。用64个bit来表示双精度。
首位为符号位s,0代表正,1代表负。
接下来的11位代表指数,将其理解为一个无符号的数字e,例如,00000000011就代表3。定义指数(阶码)M和偏置Bias,其中偏置,定义,容易看出E的范围为-1022到+1023。对于单精度,。
最后的52位是编码尾数M,第一位的权重是1/2,第二位的权重是1/4… 第52位的权重是。这里有一个隐藏位,在首位之前,代表1.因此M的范围实际上是. 当52位全为0时,M为1 当全为1时,M非常接近2,但还差了一个
浮点数. M在1到2之间,E在到,这两者配合无论是精度还是范围都足够大了。
浮点数加法(以0.2+0.4为例)
浮点数加法的计算步骤:浮点数有自己的一套计算方法,以下借助例子详细阐述,总之核心思想就是保持阶码一致,当需要移位的时候,就抛弃掉尾数的最后一位,因为这一位的权重最小,但就是抛弃尾数的最后几位导致了误差。
对阶&移位-->有效数求和-->规格化-->舍入处理-->溢出判断.
以0.2+0.4为例逐步分析。
首先,利用http://www.binaryconvert.com 将0.2和0.4转换为二进制表示,之后从二进制到十进制的逆转换同样是由这个网站完成的。
0.2:0 01111111100 1001100110011001100110011001100110011001100110011010
0.4:0 01111111101 1001100110011001100110011001100110011001100110011010
为了下面阐述方便,直接将隐藏位也一起写出来。
0.2:0 01111111100 11001100110011001100110011001100110011001100110011010
0.4:0 01111111101 11001100110011001100110011001100110011001100110011010
简单check一下,可以看出0.2的阶码E=-3,也就是1/8,乘上M后可以得到0.2;同理0.4的阶码E=-2.
1. 对阶&移位
对阶:先求阶差,明显0.2的阶码比0.4的阶码小1.
移位:小码向大码看齐,即将0.2的阶码变成-2,同时将尾数右移一位。这个操作其实就是让阶码+1,导致原数V扩大两倍,同时尾数右移一位,导致原数V缩小两倍。二者相互抵消。要注意在移动尾数时要连隐藏位一起移动,同时抛弃末位。这样一来0.2变为:
0.2:0 01111111101 01100110011001100110011001100110011001100110011001101
2. 有效数求和
将0.2和0.4的尾数求和,包含隐藏位
0.2:01100110011001100110011001100110011001100110011001101
0.4:11001100110011001100110011001100110011001100110011010
同样利用一个小网站http://www.99cankao.com 来实现这一计算,计算结果已经过手动check,为:
100110011001100110011001100110011001100110011001100111
有5位。
3. 规格化
双精度数字只允许尾数为52位,所以上述求和的数字要进行规格化,即将原来的大阶码(-2)加一,变成-1,即01111111110
同时将尾数和右移,与前面移位中类似,阶码+1让V乘以2,尾数右移让V除以2。但要注意此时右移是不包括隐藏位的,简单分析一下原因:
如果不进行规格化,相当于:
100110011001100110011001100110011001100110011001100111
中,10的权重为1,也即换位十进制为1*2+0+1=2,再加上后面的小数,我们这里假设为0.4(数字随便取的,只为了说明方便)。那么此时尾数M=2.4. 为了使其回到原本的浮点数表示,我们将阶码加一,那么相应的尾数就要除以2,变成1.2。在浮点数表示中,隐藏位始中给出一个1,就需要尾数给出0.2,这样才能得到1.2。那么自然地,100110011001100110011001100110011001100110011001100111中,黑色部分给出0.4,将其右移一位,抛弃末位,就可以得到0.2。
综上所述,规格化时尾数的移位不包括隐藏位,但是第一步移位的时候要带上隐藏位,原因是相似的,这里就不展开了。
4. 舍入处理
在对0.2规格化时,100110011001100110011001100110011001100110011001100111,末位是1,IEEE754的策略是0舍1入,因此去掉隐藏位,初位前加0,抛弃末位,并加一后变为:
0011001100110011001100110011001100110011001100110100
5. 溢出处理
整合得到最后的结果为
0 01111111110 0011001100110011001100110011001100110011001100110100
这就是我们最后得到的0.2+0.4得二进制表示,将其转换为十进制看一下结果:
0011111111100011001100110011001100110011001100110011001100110100
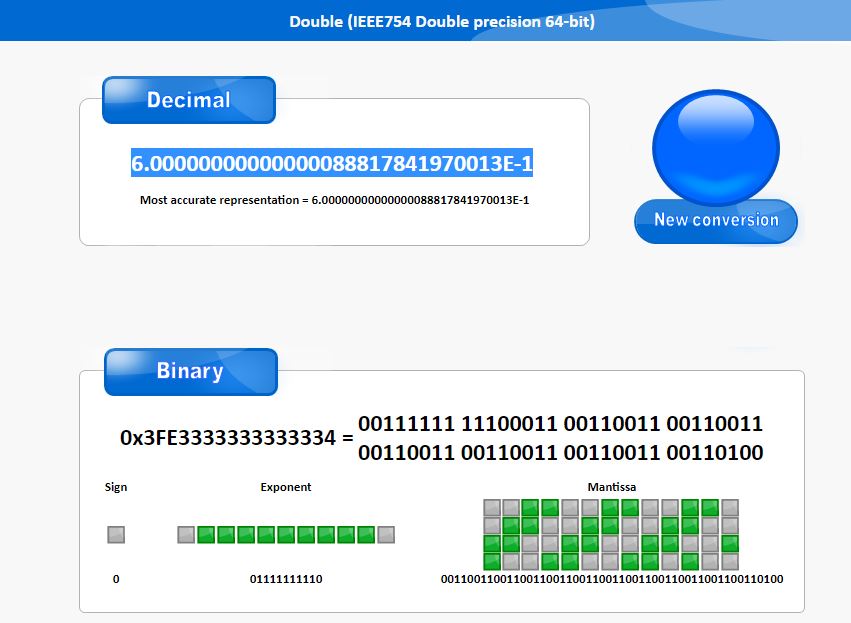
可以看出最后的结果6.00000000000000088817841970013E-1,略大于0.6,在Python中将其处理为0.6000000000000001也就很自然了。
总结
通过这个例子我们可以看出,计算机表示数字具有天然的误差,不管你采用多高的精度,多少个bit,最后至少都会产生一个的误差。