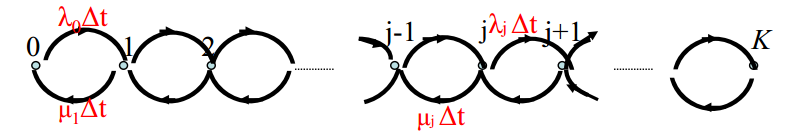版权声明:本文为博主原创文章,未经博主允许不得转载。 https://blog.csdn.net/xd15010130025/article/details/88750936
1.定义
假设系统有一状态集
E=0,1,2...K,令
N(t)表示系统在
t时刻所处的状态,则有以下结论:
pi,i+1(Δt)=P(N(t+Δt)=i+1∣N(t)=i)=λiΔt+o(Δt)
pi,i−1(Δt)=P(N(t+Δt)=i−1∣N(t)=i)=μiΔt+o(Δt)
pi,j(Δt)=P(N(t+Δt)=j∣N(t)=i)=o(Δt)∣i−j∣>2
其中,
λi>0,i=0,1,2.....K−1,μi>0,i=1,2,3....K,均为常数,则称随机过程
N(t),t>0为有限状态
E=0,1,2...K上的生灭过程。生灭过程是一个特殊的马尔科夫过程。
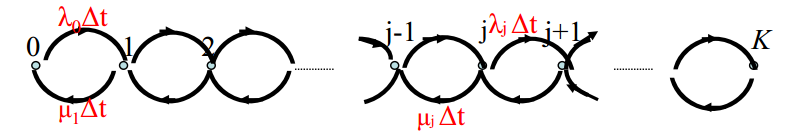
2.平稳分布
令
pj(t)=P(N(t)=j),j∈E,那么由全概率公式,有:
pj(t)=pj(t)[1−λiΔt−μiΔt−o(Δt)]+pj−1(t)[λiΔt+o(Δt)]+pj+1(t)[μiΔt+o(Δt)]+∑i−j≥2pi(t)o(Δt)
=pj(t)[1−λiΔt−μiΔt]+pj−1(t)[λiΔt]+pj+1(t)[μiΔt]
令
pj(t)=limt→+∞pj(t), {
pj,j=0,1,....K}存在,与初始条件无关,且
pj>0,∑j=0j=Kpj=1,即{
pj,j=0,1,....K}为平稳分布。
3.性质
-
pjPj,j+1=pj+1Pj+1,j
- 求各个状态的概率
结合
∑j=0j=Kpj=1可知,
pj=μ1μ2...μKλ0λ1...λK−1p0,其中
p0=1+∑i=0i=Kμ1μ2...μiλ0λ1...λi−11
4.例子
- 2-state birth-death process
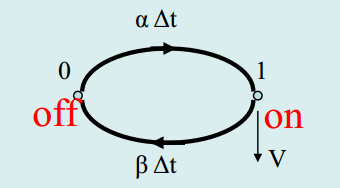
{p0+p1=1p0α=p1β⇒p0=α+ββ,p1=α+βα
- 例二
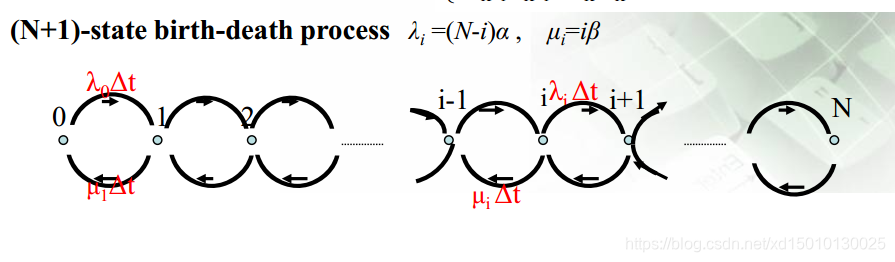
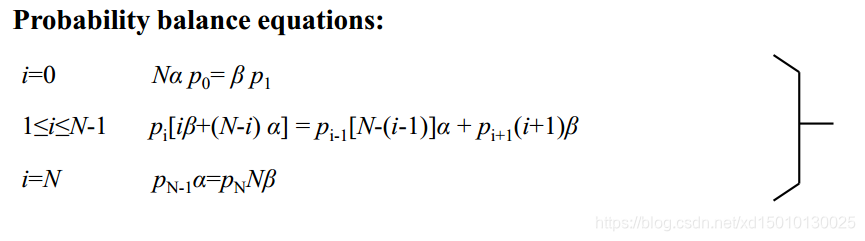

M是生成矩阵,将对应的向量相乘,我们可以得到
p0∗−Nα+p1β=0,p0∗Nα−p1[β+(N−1)α]+p32β=0…
每个矩阵都是对应状态的平衡方程。

平衡方程。