Complex Embeddings for Simple Link Prediction
来源
ICML 2016
Theo Trouillon ´ 1;2 [email protected]
Johannes Welbl3 [email protected]
Sebastian Riedel3 [email protected]
Eric Gaussier ´ 2 [email protected]
Guillaume Bouchard3 [email protected]
1 Xerox Research Centre Europe, 6 chemin de Maupertuis, 38240 Meylan, FRANCE
2 Universite Grenoble Alpes, 621 avenue Centrale, 38400 Saint Martin d’H ´ eres, FRANCE `
3 University College London, Gower St, London WC1E 6BT, UNITED KINGDOM
背景
知识图谱通过结构化的方式来表示世界知识,例如FreeBase、NELL以及谷歌知识库等,知识图谱可以用来支撑推荐系统、问答等。由于知识图谱的不完整性限制了知识图谱对上层应用的支持程度,许多科研工作者致力于知识图谱补全,其中链接预测是统计关系学习中主要的问题。链接预测自动化发现一些潜在的规则,例如通过
容易得到
,但是许多关系是不确定的,例如
不总是成立的,因此需要以概率的方式来处理包含这些实体或者关系的事实。
知识图谱二元关系中包含多类型关系,层次和组成类关系、部分/整体、严格/不严格顺序、等价关系等。对于一个关系模型需要有能力学习到上述所有的属性,例如自反性/非自反性、对称性/反对称、传递性,另外为了适应大型知识图谱,需要空间和时间代价线性的。
embedding 的点积形式可以处理对称关系和反身性,使用恰当的损失函数可以处理传递性,但是对于反对称性需要爆炸性的参数,使得模型容易过拟合。本文讨论使用复值embedding方法,可以捕捉反对称关系,并且保持点积的效率不变,时间空间线性。
使用低秩正规矩阵的实部作为关系
建模关系:
两个实体之间的关系可以使用二元值来表示
,
表示头实体,
是尾实体,概率可以用逻辑反向链接函数:
是打分的潜在矩阵,
是部分观察到的符号矩阵
目标是找到
一般结构来近似现实世界中的关系,标准的矩阵分解
来近似
。
和
是两个独立的矩阵
,
是矩阵的秩。按照这种方式分解假设实体出现在头实体和尾实体是不同的,也就是说相同的实体具有不同的embedding,依赖于出现在头实体还是尾实体。
为了在头实体和尾实体中使用相同的embedding,研究者将点积形式一般化尾打分函数,或者叫做组成函数。

对于左右因子使用相同的embedding归结为特征值分解,通常用来近似实对称矩阵
\begin{equation}
\label{eq:1}
\end{equation}
所有的特征值和特征向量属于实空间,
是正交的。
然而,本文所考虑的问题是矩阵是反对称的,也就是说矩阵所代表的关系是反对称的,在实数空间中的特征值分解是不能做到的,因此考虑在复空间中分解。定义复空间中的内积运算:
即使复特征向量
,在特征值分解中
的逆计算会占据很大的计算开销。数学上定义了一类矩阵避免我们去计算特征向量矩阵的逆,这类矩阵叫做正规矩阵,对于一个复数矩阵
,如果满足
。正规矩阵的谱定理表明了这一点:
其中的矩阵
是特征值按照模大小顺序组成的对角矩阵。
是特征向量组成的酉矩阵。酉矩阵满足
。
实数正规阵包含所有的对称和反对称的符号矩阵,正交矩阵和许多其他可以代表二元关系的矩阵,但是有很多
形式的矩阵并不是纯实数的,而公式中
必须是纯实数,因此这里简单的处理为保留分解的实数部分:
低秩分解
在链接预测任务中关系矩阵是未知的,目标是从有噪声的观察到内容中重建它,为了使模型是可以学习的,也即一般化为观察到的链接,一些常规的假设是必须的。因为我们处理二元关系,因此假设它们有低符号秩。符号矩阵
的符号秩定义为和
有相同符号模式的实矩阵秩的最小值:
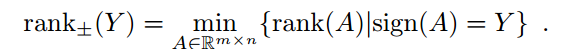
如果可观察矩阵
是低符号秩的,我们的模型可以使用秩最多为它二倍的矩阵分解它,也就是说杜宇任意的
,总存在一个矩阵
,并且有
,
的秩最多为
的符号秩的2倍。
当
的秩为
时,矩阵
的对角线元素前K个非零的,可以直接得到
,
。单独实体s和o之间的单个关系的打分
可以使用下面的方式来打分:
二元多关系数据上的应用
上面的章节主要是对关系的一个类型建模,接下来将扩展模型到关系的多个类型。
我们的目标是对于所有的关系
,重建打分矩阵
。对于给定的两个实体
和
,事实
为真的概率为:
是基于观察到关系分解的打分函数,
表示模型的参数。当
作为一个整体是未知的时候,我们假设可以观察到的真实和错误的事实
, 对应部分可以观察到不同关系的邻接矩阵,
是可以观察到的三元组,目标是对于未观察到的三元组判断是否成立。
依赖于不同的打分函数
来预测张量
中的项,可以得到不同的模型,本文的打分模型:
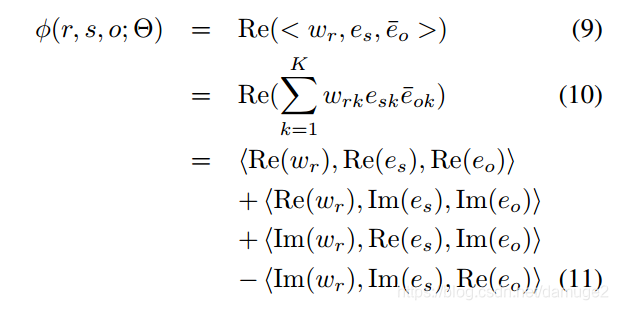
通过分离一个关系embedding的实虚部,我们可以获得一个关系矩阵分解的实部和虚部
,
.
是对称的,但是
是反对称的,因此这使我们能够准确地描述实体对之间的对称和反对称关系,同时仍然使用实体的联合表示,无论它们是关系的主体还是对象。
损失函数
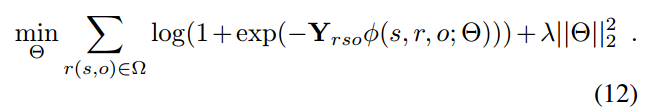
对应embedding
实验部分
数据集:
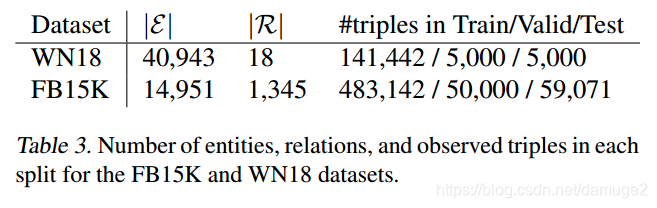
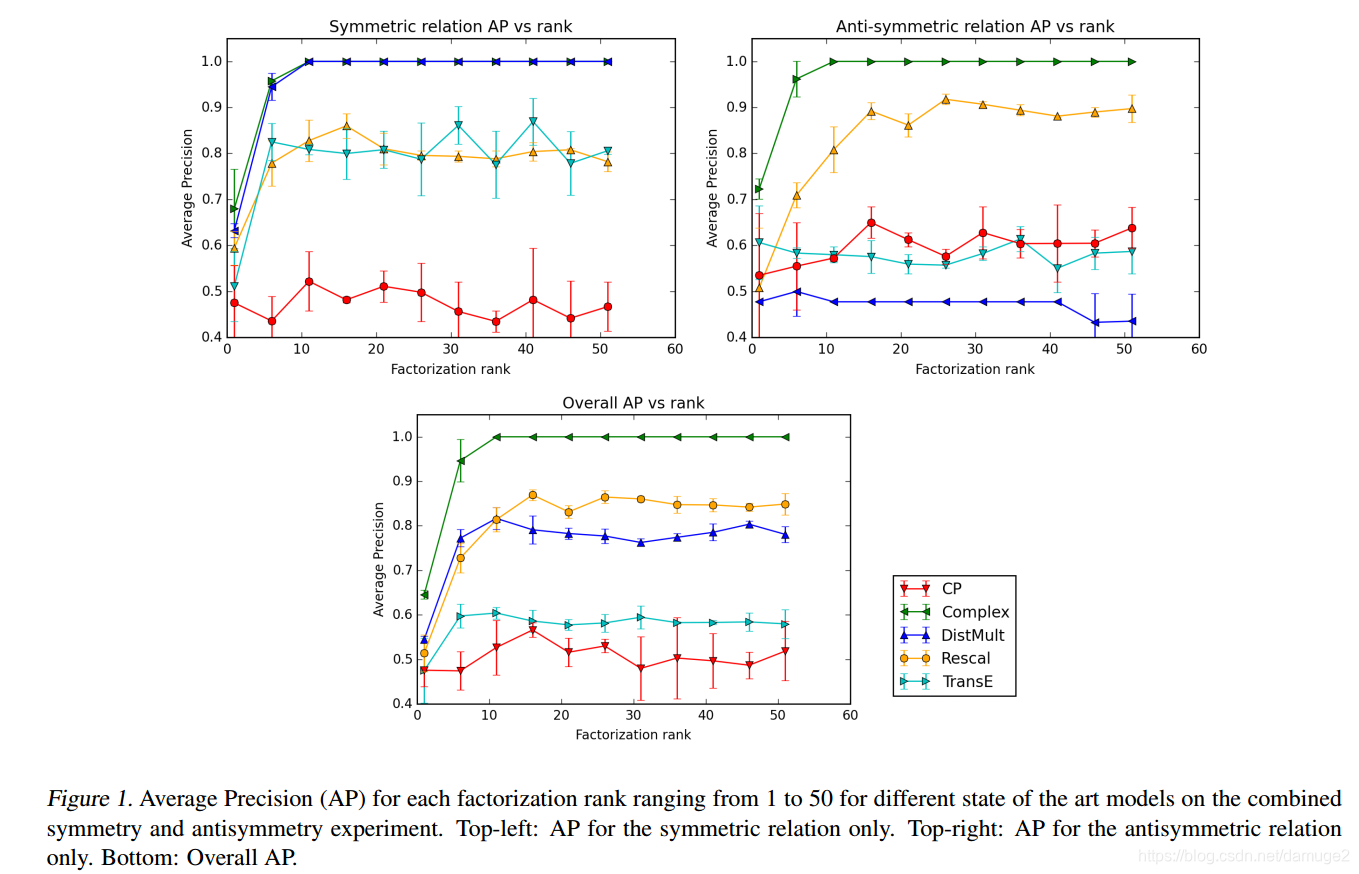
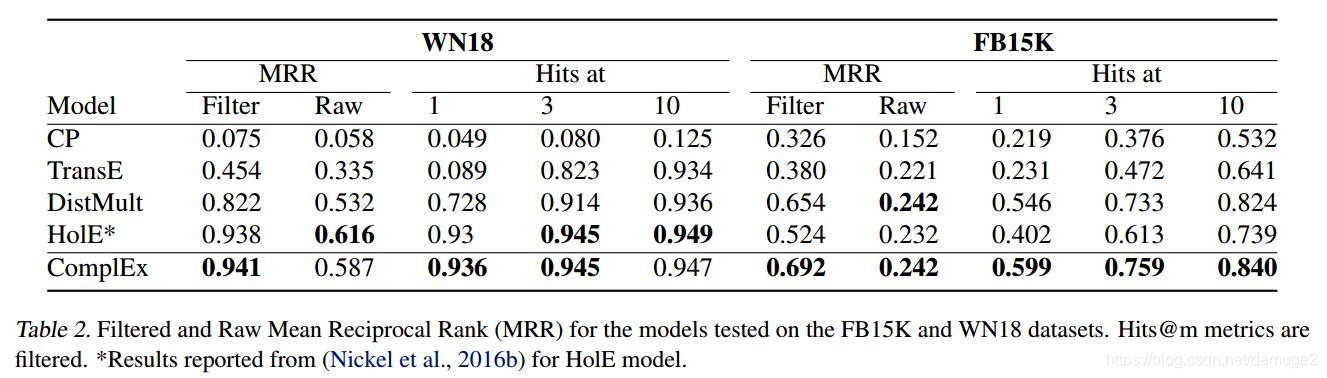
filter: 在从排名中删除出现在训练,验证或测试集中的所有其他正观察到的三元组之后计算,而原始指标不会删除这些。
负采样的影响:
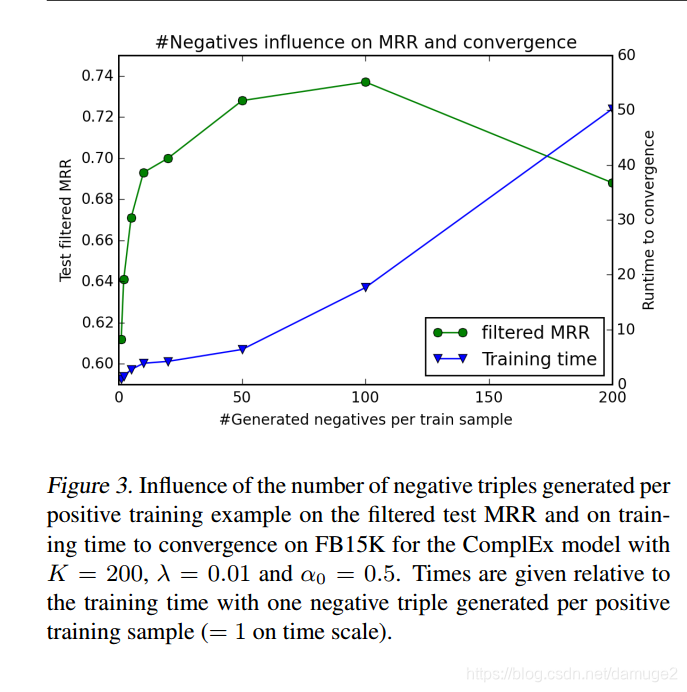
代码
附录
低秩分解: