A. Sushi for Two
题意
在一个 01 序列中找出长为偶数的连续的一段使得它前一半和后一半内部分别相同,而前一半和后一半不同。
\(2\le n\le 100\ 000\)
题解
令共有 \(k\) 段连续的区间,第 \(i\) 段区间的长度设为 \(a_i\),则答案是在求 \(\max_{i=1}^{k-1}\min(a_i,a_{i+1})\)。我因为没好好判 \(\min\) 而轻松地丢掉了 WA on pretest 4 的50分。
代码
标签
- 枚举
B. Circus
题意
有 \(n\) 个人,需要把它们分成两组,每组恰好 \(\frac n2\) 个人。每个人可能会技能 \(1\) 或技能 \(2\),一个人可能会其中一种、两种都会或什么都不会。
要求第一组中会技能 \(1\) 的人数恰好等于第二组中会技能 \(2\) 的人数,输出方案。
\(2\le n\le 5\ 000\)
题解
\(O(n^2)\) 的做法其实有些冗余,所以找到一种好理解的 \(O(n)\) 算法。
我们用两个 0/1 来表示一个人会的技能。比如一个人会技能 \(1\) 而不会技能 \(2\) 则表示为 0 1。
由于 1 1 的限制比较大,而他在第一组或第二组都必须做出贡献,因此我们枚举 1 1 在第一组有 \(i\) 个,假定总共有 \(d\) 个 1 1,则钦定第二组有 \(k-i\) 个 1 1。
此时我们首先要把贡献较小的一边给补成 \(\max(i,d-i)\) 个,然后会分别剩下 \(a\) 个 0 0,\(b\) 个 0 1,\(c\) 个 1 0。
如果 \(b>c\),可以考虑把 \(b\) 多出来的 \(b-c\) 个塞给第一组,则不做出任何贡献。
同理如果 \(c>b\),可以考虑把 \(c\) 多出来的 \(c-b\) 个塞给第二组,则不做出任何贡献。
但是会有一种情况,导致 \(\max(i,d-i)+|b-c|>\frac n2\),此时就会有一些不得不做贡献的人,理解为溢出。此时就会产生一些不得不做的贡献,是无论如何都补不回来的。
因此,当 \(\max(i,d-i)+|b-c|\le \frac n2\) 时,就有解。我们首先把 \(i\) 个 1 1 输出,如果 \(i<d-i\),需要先用 1 0 把它补到 \(d-i\),这也是要输出的。然后剩下的优先选 0 1 输出,最后拿 0 0 补齐。
代码
标签
- 枚举
- 构造
C. Skyscrapers
题意
在 \(n\times m\) 的网格上,每个格子都有一个权值。现在对于每个格子 \((i,j)\),问给第 \(i\) 行和第 \(j\) 列重新赋值为正整数,使得它们的原相对大小不变,问最大的正整数最小是多少。
\(1\le n,m\le 1\ 000\)
题解
我们发现第 \(i\) 行和第 \(j\) 列仅在 \((i,j)\) 处产生联系,其余都是独立的。
因此对于所有元素,可以在 \(O(nm\log n)\) 的时间里知道它在那一行/那一列的排名,行和列、大的和小的都要照顾到。假设它在那一行里排名为 \(p\),那一列里排名为 \(q\),则答案为 \(\max(p,q)+\max(m-p,n-q)\)。
代码
标签
- 排序
- 贪心
D. Camp Schedule
题意
给定串 \(s\),代表学生的计划,其中 0 表示这一天没写作业,1 表示这一天写作业了。
给定串 \(t\),代表最佳计划,其中 0 表示这一天不用写作业,1 表示这一天要写作业。
你可以改变串 \(s\) 的顺序,最大化 \(t\) 在 \(s\) 中出现的次数。
\(1\le |s|,|t|\le 500\ 000\)
题解
可以看出给出 \(s\) 相当于给出了 \(0\) 和 \(1\) 的个数,因此我们需要考虑 \(t\) 的构造。我们发现 \(t\) 在 \(s\) 中的出现是可以重合的,因此我们求出 KMP 中的 \(nxt\) 数组,我们只取前 \(n-nxt[n]\) 个。假设前 \(n-nxt[n]\) 个字符构成的字符串为 \(u\),令 \(u\) 中 \(0\) 的个数为 \(p\),\(1\) 的个数为 \(q\);令 \(s\) 中 \(0\) 的个数为 \(a\),\(1\) 的个数为 \(b\),则至少能构成 \(\min\left(\left\lfloor\frac ap\right\rfloor,\left\lfloor\frac bq\right\rfloor\right)-1\) 个 \(t\) 。
把这些构造完后,我们还会剩下一些 \(0,1\),而且还有一个 \(t\) 是不完整的,我们尽量与 \(t\) 匹配地接在它后面。这样输出就可以了。
求 \(nxt\) 数组和构造时间复杂度为 \(O(\mathtt{strlen}(s))\)。
代码
标签
- KMP
- 构造
E. Museums Tour
题意
一周有 \(d\) 天。一个人在一周的第 \(1\) 天从 \(1\) 号点出发,城市的地图是一个 \(n\) 个点 \(m\) 条边的有向图。这个人每天晚上要么结束旅行,要么往某个方向行走一步。每个城市有一个博物馆,只在每周的特定时间开放。问他最多能参观多少个城市的博物馆。
\(1\le d\le 50\)
\(1\le n\le 100\ 000\)
\(1\le m\le 100\ 000\)
题解
好题。
我们考虑把每一天拆成 \(d\) 个点,令第 \(i\) 号点在第 \(j\) 天的点为 \([i,j]\)。存在 \(\left<i,v\right>\),则让 \([i,j]\) 向 \([v,j\bmod d+1]\) 连边。
注意:博物馆不开放仅代表不做出贡献,不代表那天不能去那个城市。因此连边不能省。
然后我们可以在这个有向无环图上跑 tarjan 缩点。
可以证明,在新的 DAG 上的任意一条链中,原图的每个点只会出现在一个强连通分量里。
- 在连边后的图上,如果原图中的点 \([i,j]\) 向 \([i,k]\) 有连边,那么 \([i,k]\) 一定向 \([i,j]\) 有连边。因此在路径上可能出现的原图同一个点的新点都会被缩到同一个强连通分量里。
因此我们可以计算每个 SCC 的贡献。当给出的矩阵中 \([i,j]\) 为 \(1\) 时则做出 \(1\) 的贡献,\(i\) 相同的不重复统计。
然后计算从 \([1,1]\) 开始的权值最长路。拓扑排序可以完成。
但是由于一共有 \(5\times 10^6\) 个点,递归可能会爆栈,因此我写的非递归(码量有点大但是不是很难写)。
可以参考 Pinkrabbit 的递归超小空间解法。
代码
标签
- tarjan
- 拓扑排序
F. Cooperative Game
题意
交互题
现在有 \(10\) 个棋子。有一个图,是由一条长为 \(t\) 个节点的链指向一个大小为 \(c\) 的有向环的。其中除了 home vertex的入度为 \(0\),finish vertex 的入度为 \(2\),其余各点的入度均为 \(1\);同时,所有点的出度都为 \(1\)。
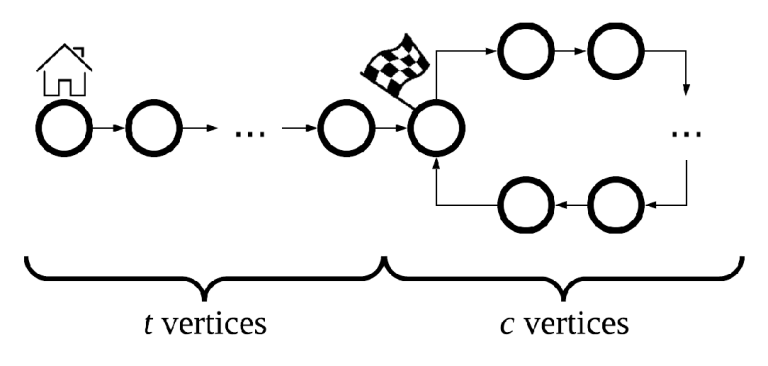
现在,每一步你可以选取一些点让它走一步到它出边指向的点。走完每一步以后,交互器都会告诉你哪些棋子在同一个点上。现在要你在 \(3(t+c)\) 步以内,把所有的棋子都移动到 finish vertex。
\(1\le t,c,(t+c)\le 1\ 000\)
题解
由于之前做过的交互题都是和倍增/二进制有关,本题给出了 \(10\) 个点,而且 \(\log_2 1000\) 也恰好是 \(10\),于是就这样陷进去了…
实际上我们只需要 \(3\) 个点就能解决本题的问题,我们可以把这 \(10\) 个点分为 \(0,1,23456789\) 三个部分。
首先让 \(0\) 每走 \(2\) 步,\(1\) 走一步。当 \(0,1\) 相遇时环长即为 \(0\) 走过的距离减去 \(1\) 走过的距离。每次 \(0\) 总比 \(1\) 快一步。除了一种情况以外,环长也等于 \(1\) 走过的步数。这叫做Floyd判环。
一种情况:
如果下一步是 \(0,1\) 一起走的话,那么 \(0\) 走的步数就不恰好是 \(1\) 走的步数的两倍了,因此需要判一下。
此时我们知道 \(0,1\) 在环上的某个点相遇了。我们现在知道了环长 \(c\) 和链长 \(t\),但是我们不知道 finish vertex 在哪里。
我们为了让 \(01\) 与 \(23456789\) 在 finish vertex 相遇,我们可以构造出环上的一个点。设 \(1\) 号棋子已经走了 \(m\) 步,因此令 \(01\) 在环上“倒退 \(m\) 步”,也就是前进 \(-m\pmod c\) 步,此时就和 \(23456789\) 同步了。我们发现,环长一般情况下也恰好是 \(m\)(特殊情况是 \(m+1\),让 \(01\) 先走一步就可以了),然后让 \(0123456789\) 同时移动。
最终所有点相遇的地方就是 finish vertex 了。输出 done 即可。
一般情况下步数为 \(2(t+c)-1\),上面提到的情况步数为 \(2(t+c)\)。
代码
标签
- Floyd判环
- 交互
