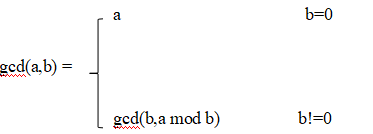一.题目分析求最大公约数。
程序还需要实现每个算法下的不同规模数据的平均运行时间。
算法介绍如下:
1. 辗转相除法(欧几里德法)
程序还需要实现每个算法下的不同规模数据的平均运行时间。
2.穷举法穷举法(也叫枚举法)
穷举法求两个正整数的最大公约数的解题步骤:从两个数中较小数开始由大到小列举,直到找到公约数立即中断列举,得到的公约数便是最大公约数 。对两个正整数a,b如果能在区间[a,0]或[b,0]内能找到一个整数temp能同时被a和b所整除,则temp即为最大公约数。
3.更相减损法(等值算法)
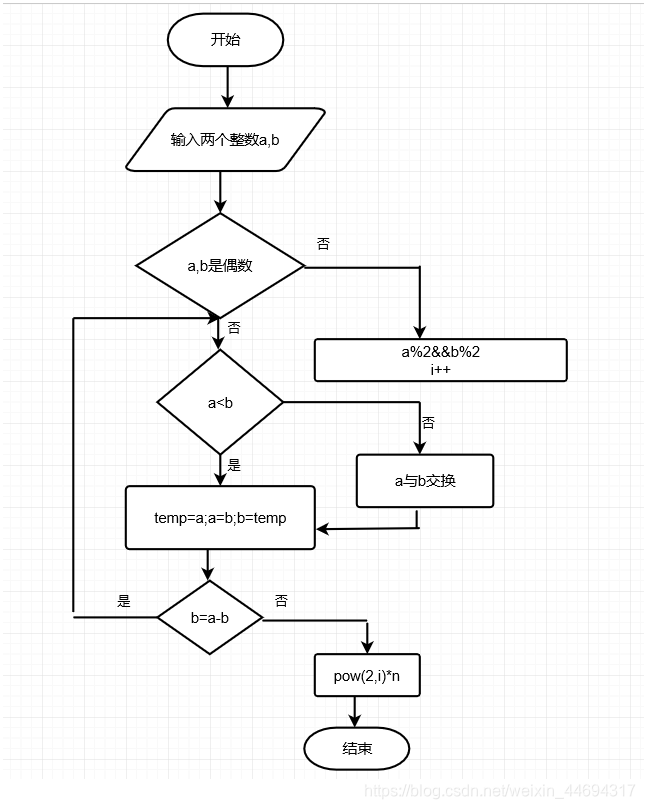
第一步:任意给定两个正整数;判断它们是否都是偶数。若是,则用2约简;若不是则执行第二步。
第二步:以较大的数减较小的数,接着把所得的差与较小的数比较,并以大数减小数。继续这个操作,直到所得的减数和差相等为止。则第一步中约掉的若干个2与第二步中等数的乘积就是所求的最大公约数。
其中所说的“等数”,就是最大公约数。求“等数”的办法是“更相减损”法。所以更相减损法也叫等值算法。
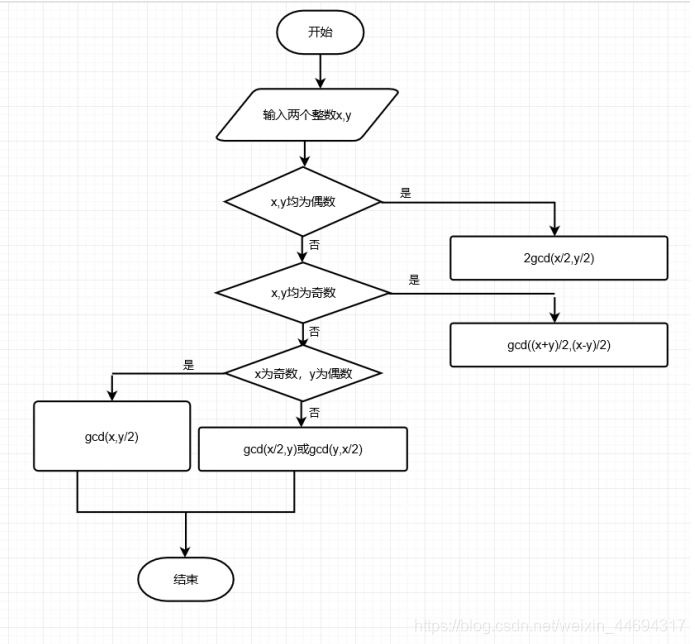
4.Stein算法
Stein算法由J. Stein 1961年提出,这个方法也是计算两个数的最大公约数。来研究一下最大公约数的性质,发现有 gcd( kx,ky ) = k*gcd( x,y ) 这么一个非常好的性质。试取 k=2,则有 gcd( 2x,2y ) = 2 * gcd( x,y )
整理一下,对两个正整数 x>y :
1.均为偶数 gcd( x,y ) =2gcd( x/2,y/2 );
2.均为奇数 gcd( x,y ) = gcd( (x+y)/2,(x-y)/2 );
2.x奇y偶 gcd( x,y ) = gcd( x,y/2 );
3.x偶y奇 gcd( x,y ) = gcd( x/2,y ) 或 gcd( x,y )=gcd( y,x/2 );
现在已经有了递归式,还需要再找出一个退化情况。注意到 gcd( x,x ) = x ,就用这个。
二.算法构造
各个算法的流程图:
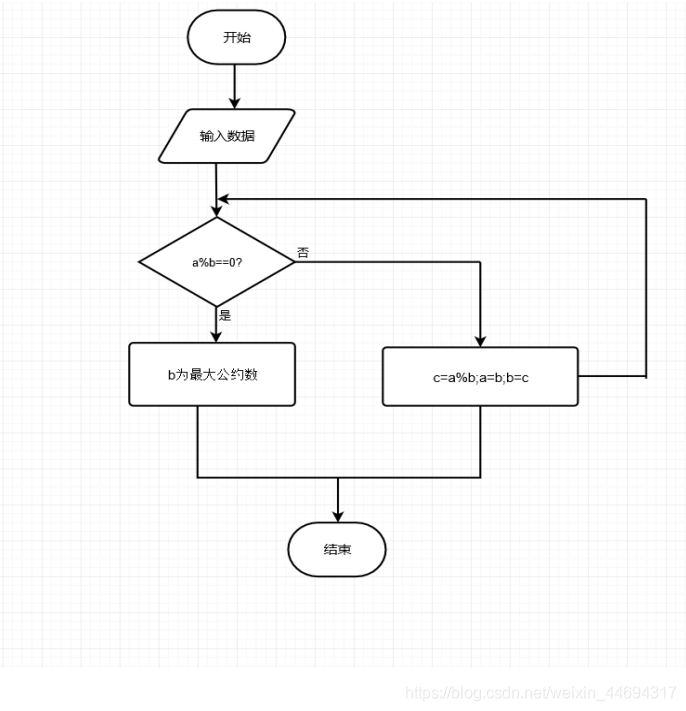
1.辗转相除法(欧几里德法)
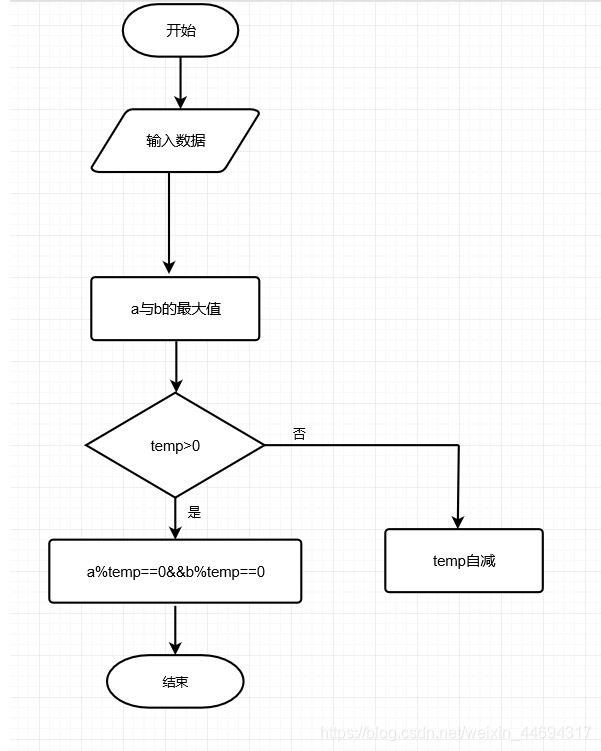
2.穷举法
3.更相减损法(等值算法)
4.Stein算法
三.算法实现
//求最大公约数
//算法:1.辗转相除法(欧几里德法) 2.穷举法 3.更相减损法(等值算法) 4.Stein算法
//Dream 张
//2019-3-8
#include<iostream>
#include<stdlib.h>
#include<string>
#include<math.h>
#include <ctime>
using namespace std;
int maxgysarray1(int a[],int); //求数组的最大公约数
int maxgysarray2(int a[],int);
int maxgysarray3(int a[],int);
int maxgysarray4(int a[],int);
//1.辗转相除法求两数的最大公约数
int gcd1(int a,int b) //函数嵌套调用
{
int temp; //定义整型变量
if(a<b) //通过比较求出两个数中的最大值和最小值
{
temp=a;a=b;b=temp;
} //设置中间变量进行两数交换
while(b!=0) //通过循环求两数的余数,直到余数为0
{
temp=a%b;
a=b; //变量数值交换
b=temp;
}
return (a); //返回最大公约数到调用函数处
}
//2.穷举法(枚举)
int enumer (int a,int b) //自定义函数求两数的最大公约数
{
int temp; //定义义整型变量
temp=(a>b)?b:a; //采种条件运算表达式求出两个数中的最小值
while(temp>0)
{
if (a%temp==0&&b%temp==0) //只要找到一个数能同时被a,b所整除,则中止循环
break;
temp--; //如不满足if条件则变量自减,直到能被a,b所整除
}
return (temp); //返回满足条件的数到主调函数处
}
//3.更相减损法(等值算法)
int gcd(int m,int n)
{
int i=0,temp,x;
while(m%2==0 && n%2==0) //判断m和n能被多少个2整除
{
m/=2;
n/=2;
i+=1;
}
if(m<n) //m保存大的值
{
temp=m;
m=n;
n=temp;
}
while(x)
{
x=m-n;
m=(n>x)?n:x;
n=(n<x)?n:x;
if(n==(m-n))
break;
}
if(i==0)
return n;
else
return (int )pow(2,i)*n;
}
//4.Stein算法
int Stein1(unsigned int x,unsigned int y) //函数非递归调用
{ //返回最大公约数x和y
int factor=0;
int temp;
if(x<y)
{
temp=x;
x=y;
y=temp;
}
if(0==y)
{
return 0;
}
while(x!=y)
{ //当x时偶数时
if(x&0x1)
{
if(y&0x1)
{ //当x和y都是偶数时
y=(x-y)>>1;
x-=y;
}
else
{ //当x是偶数,y是奇数
y>>=1;
}
}
else
{ //当x是奇数
if(y&0x1)
{
x>>=1;
if(x<y)
{
temp=x;
x=y;
y=temp;
}
}
else
{ //当x和y都是奇数
x>>=1;
y>>=1;
++factor;
}
}
}
return (x<<factor);
}
int maxgysarray1(int a[],int num) //求辗转相除法数组的最大公约数
{
int max1;
max1=gcd1(a[0],a[1]);
for(int i=1;i<=num-1;i++)
max1=gcd1(max1,a[i]);
return max1
}
int maxgysarray2(int a[],int num) //求穷举法数组的最大公约数
{
int max2;
max2=enumer(a[0],a[1]);
for(int i=1;i<=num-1;i++)
max2=enumer(max2,a[i]);
return max2
}
int maxgysarray3(int a[],int num) //求更相减损法数组的最大公约数
{
int max3;
max3=gcd(a[0],a[1]);
for(int i=1;i<=num-1;i++)
max3=gcd(max3,a[i]);
return max3
}
int maxgysarray4(int a[],int num) //求Stein算法数组的最大公约数
{
int max4;
max4=Stein1(a[0],a[1]);
for(int i=1;i<=num-1;i++)
max4=Stein1(max4,a[i]);
return max4;
}
int main()
{
int x,y,m,n,i;
int abc[10]={6,12,18,24,30,36,42,48,54,60}; //定义数组
//int abc[25]={2,4,6,8,10,12,14,16,18,20,22,24,26,28,30,32,4,36,38,40,42,44,46,48,50};
clock_t start,finish; //clock_t是用来保存时间的数据类型,是一个长整形数
double duration;
cout<<"****** 1.辗转相除法(欧几里德法) ******"<<endl;
cout<<"****** 2.穷举法 ******"<<endl;
cout<<"****** 3.更相减损法(等值算法) ******"<<endl;
cout<<"****** 4.Stein算法 ******"<<endl;
cin>>i;
if(i>4)
cout<<"输入正确的数:"<<endl;
start = clock(); //计时函数:clock()
for(m=0;m<10;m++)
//for(m=0;m<25;m++ )
switch(i)
{
case 1:cout<<"最大公约数为:"<<maxgysarray1(abc,10)<<endl;break;
case 2:cout<<"最大公约数为:"<<maxgysarray2(abc,10)<<endl;break;
case 3:cout<<"最大公约数为:"<<maxgysarray3(abc,10)<<endl;break;
case 4:cout<<"最大公约数为:"<<maxgysarray4(abc,10)<<endl;break;
default:cout<<"error"<<endl;
}
finish = clock();
duration = (double)(finish-start)/CLOCKS_PER_SEC; /*常量CLOCKS_PER_SEC,用来表示一秒钟会有多少个时钟计时单元。*/
cout<<"运行程序所用的时间为:"<<duration<<"seconds."<<endl;
return 0;
}
*四.测试及运行结果
在这里我只列出部分运行结果。
-
辗转相除法(欧几里德法)
十组数据所用的时间:0.005s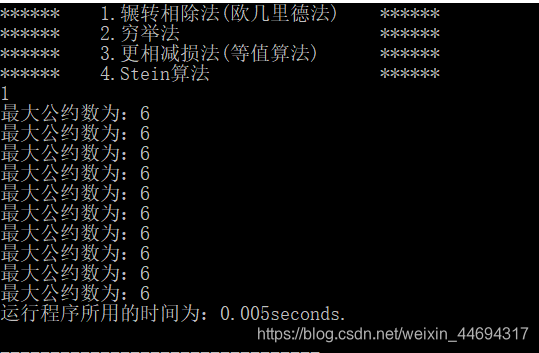
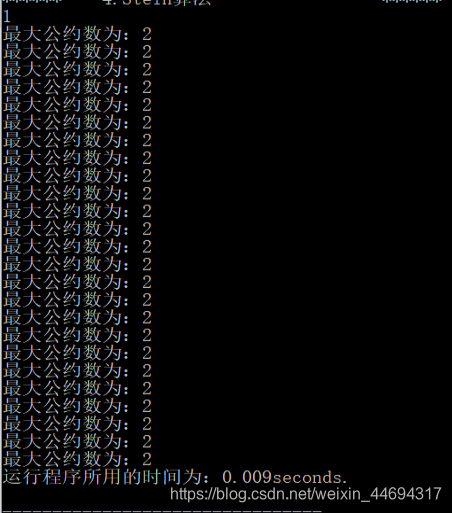
二十五组数据所用的时间:0.009s
-
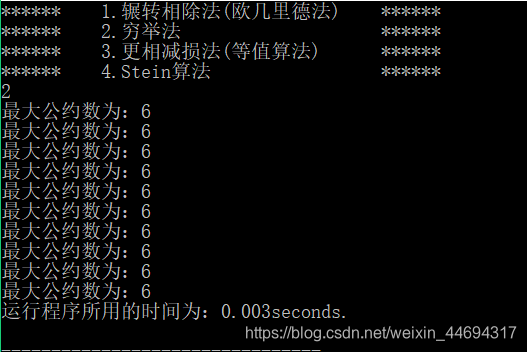
穷举法
十组数据所用的时间:0.003s
二十五组数据所用的时间:0.01s

五.经验归纳
第一,我想说一下就是时间函数的运用,我在网上参考了好多资料,有好几种时间函数的用法:clock()函数,它的应用方法是:
void time1()
{
double dur;
clock_t start,end;
start = clock();
调用你所要求时间的函数 ;
end = clock();
dur = (double)(end - start);
printf("Use Time:%f\n",(dur/CLOCKS_PER_SEC));
}
timeGetTime()函数:
void time2()
{
DWORD t1,t2;
t1 = timeGetTime();
调用你所要求时间的函数 ;
t2 = timeGetTime();
printf("Use Time:%f\n",(t2-t1)*1.0/1000);
}
还有其它一些方法我就不说了。
第二,就是求数组的最大公约数。我从网上找到了用辗转相减法求数组的最大公约数,于是我就参考着把其他几种方法的也求出来了。
例如运用辗转相除法:
int maxgysarray(int a[],int num)
{
int max;
max=gcd(a[0],a[1]);
for(int i=1;i<=num-1;i++)
max=gcd(max,a[i]);
return max;
}
第三,我想说代码的测试,一开始我是不会测试代码的,但我在博客上就搜索怎么样去测试,然后自己尝试着去测试。尽管在这个过程中有许许多多的问题,但我最终解决了,并且也学会了去测试代码。
第四,我想说一说这次的收获。通过这次的学习,我知道了利用时间函数直接求程序运行时间,这样可以节省好多时间。虽然这个程序里还有好多我没有掌握的,但我会尽自己最大的努力去理解它,争取能够自己写下来。中间虽然出现了许许多多的问题,但我通过查阅资料,与同学讨论,最终解决了。但是结果却不是很满意,希望自己以后多多努力!