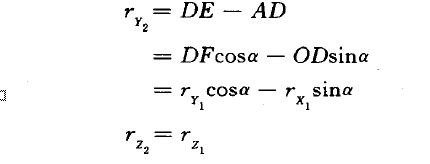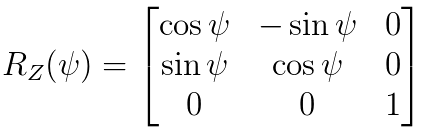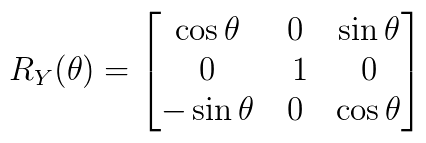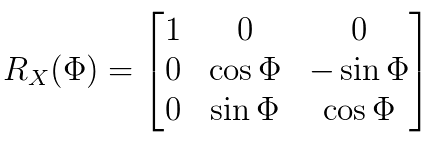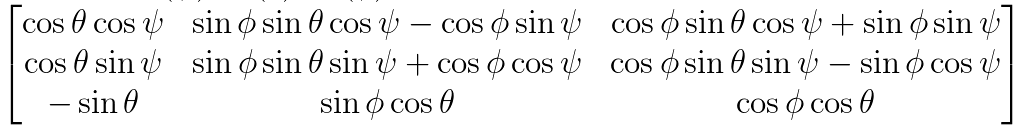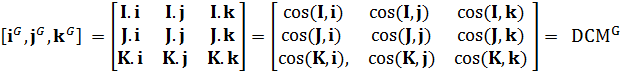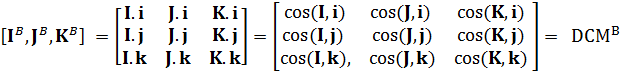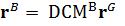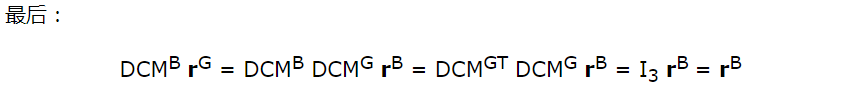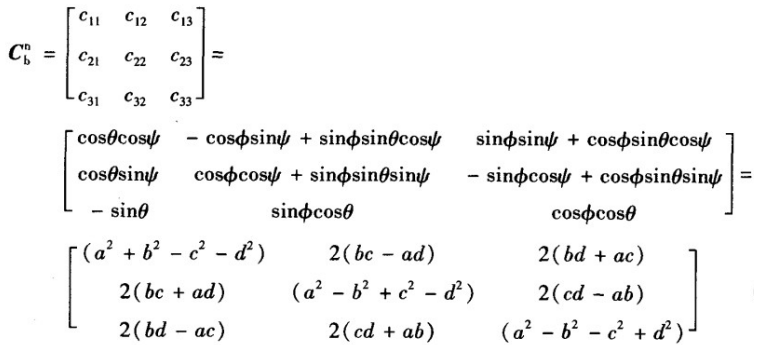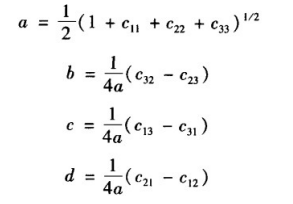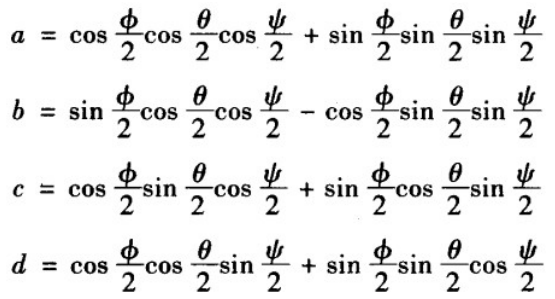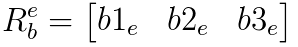SLAM中三维空间的刚体运动描述方式
1. 旋转矩阵
1.点和向量,坐标系
- 点:在几何学上点是 没有大小而只有位置,即点存在于三维空间中的某一个位置。
- 向量: 可以形象化地表示为 带箭头的线段。箭头所指:代表向量的方向;线段长度:代表向量的大小。 (请勿将向量 与它的 坐标 两个概念混淆,只有确定向量所在的坐标系,才能讨论它在该坐标系下的坐标)
- 定义坐标系后,也就是一个线性空间的基 (e1,e2,e3),向量a在该坐标系下的坐标为:

- 左手坐标系 和 右手坐标系(更为常见)

- 向量的运算
1. 加减法
2. 内积(inner product): 可以描述向量间的投影关系
对于 a,b∈R3,内积可以表示为:
![]()
3.外积,亦称叉乘(cross product)
1) 对于 a,b∈R3,外积可以表示为:

式中 ∧ 为反对称符号(可以读作“上尖”),a∧表示向量 a 的 反对称矩阵。
2)外积可以表示向量的旋转:向量 a 到 b 的旋转向量 w 的方向就是 a×b的方向

2、坐标系间的欧氏变换
对于同一个向量 p,它在世界坐标系下的坐标 pw和在相机坐标系下的坐标 pc是不同的,它们的变换关系由两坐标系间的变换矩阵 T 来描述。(如下图所示,下图来自视觉SLAM十四讲 图3-2)

- 欧氏变换 = 旋转 + 平移
- 旋转
设某个单位正交基 (e1,e2,e3) 经过一次旋转变成 (e1′,e2′,e3′)。对于同一个向量 a(该向量不会因坐标系的旋转而发生运动),它在两个坐标系下的坐标分别为 [a1,a2,a3]T 和 [a1′,a2′,a3′]T,两坐标点满足:

式 (3.4) 左右两边同时左乘 ![]() ,得
,得

式 (3.5) 中的旋转矩阵 R 的特殊性质:
旋转矩阵是行列式为 1 的正交矩阵
旋转矩阵的逆为自身转置,逆矩阵 RT 表示一个相反的旋转
旋转矩阵的集合定义为:
![]()
SO(n)是特殊正交群(Special Orthogonal Group),SO(3) 就是由三维空间的旋转矩阵组成。
- 平移
向量 a经过一次旋转 R 和一次平移 t 后,得到 a′ :
a′=Ra+t
所以,两个坐标系的刚体运动可以由 R 和 t完全描述。
3.变换矩阵与齐次坐标
欧氏变换多次之后的变换矩阵表示过于复杂,引入齐次坐标和变换矩阵重写式 (3.7):
![]()
式 (3.8) 中的 T 称为变换矩阵,这种矩阵又称为特殊欧式群(Special Euclidean Group):

与 SO(3) 一样,该矩阵的逆表示一个反向的变换:

什么是姿态解算:
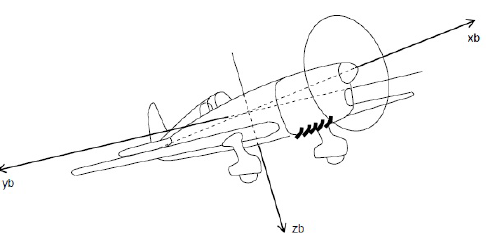
飞行器的姿态解算过程涉及到两个坐标系,一个是运载体的机体坐标系,该坐标系与运载体固连,当运载体转动的时候,这个坐标系也跟着转动,我们假设运载体的坐标系为b系。另外一个是地理坐标系,即东北天坐标系,X轴指向东,Y轴指向北,Z轴指向天,这个坐标系也称为导航坐标系,我们假设这个坐标系为n系。
所谓的姿态解算,就是求出飞行器当前的姿态,也就是求出飞行器上固连的机体坐标系b相对于地理坐标系n的变化。由于n系和b 系均为直角坐标系,各轴之间始终保持直角,所以可将坐标系理解成刚体,当只研究两个坐标系间的角位置关系时,可对一个坐标系作平移,使其原点与另一个坐标系的原点重合。因此,两坐标系间的空间角位置关系可理解成刚体的定点转动。而刚体定点转动这个变化可以通过一个变换矩阵来表示,这个矩阵包含了刚体的所有姿态信息。对于飞行器来说,可以根据这个变换矩阵求出偏航角、俯仰角、翻滚角。可以这么理解这个变换矩阵:对于机体坐标系中的一个向量,当它左乘这个变换矩阵之后,就能得出这个向量在地理坐标系中的大小。
由b系到n系的坐标变换短阵也称为运载体的姿态矩阵,而我们姿态解算的目标就是根据惯性器件的输出实时计算出这个姿态矩阵,从而实时获取飞行器当前的偏航、俯仰角、翻滚角。陀螺和加速度计分别用来测量运载体的角运动信息和线运动信息,根据陀螺仪和加速度计的输出,我们就能实时跟新这个姿态矩阵。在姿态解算中,
用来表示姿态矩阵的方式有三种,分别是欧拉角、方向余弦、四元数。下面我们一一介绍。
欧拉角表示姿态矩阵:
以下来自秦永元的《惯性导航》。
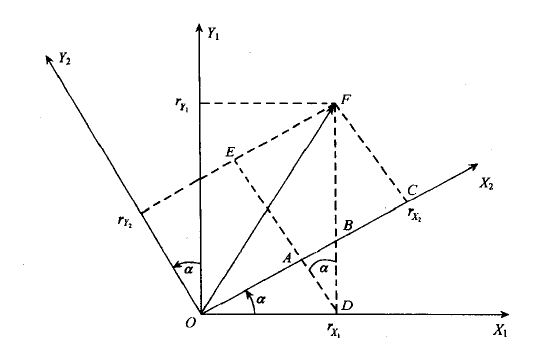
1、坐标系旋转:
该式描述了同一矢量在不同坐标系内投影间的变换关系,C称为从坐标系1至坐标系2的变换短阵。上述变换关系分析中,坐标系2是经坐标系1仅绕Z1轴旋转α角后获得的,为便于叙述,称仅绕一根轴的旋转为基本旋转。两坐标系间任何复杂的角位置关系都可以看作有限次基本旋转的复合,变换矩阵等于基本旋转确定的变换短阵的连乘,连乘顺序依基本旋转的先后次序由右向左排列。例如运载体的空间姿态可看作依次绕偏航轴、俯仰轴、翻滚轴作基本旋转后的复合结果。
2、用欧拉角表示旋转矩阵:
对于飞行器而言,由地理坐标系O-XeYeZe向机体坐标系O-ZbYbZb到的变换过程可以分为三步(假设初始时机体坐标系和地理坐标系重合):
1)第一步是绕机体坐标系的Z轴逆时针旋转,得到偏航角Yaw,大小为Ψ,旋转矩阵(这里是从机体坐标系变为地理坐标系的反向旋转矩阵,注意与上面的坐标变换区分)为:
假设旋转前向量为X0, 旋转后坐标向量为X1,则X0 = Rz(Ψ) * X1 。
2)第二步是绕机体坐标系的Y轴逆时针旋转,得到俯仰角Pitch,大小为θ,旋转矩阵为(这里是从机体坐标系变为地理坐标系的反向旋转矩阵):
假设旋转前向量为X1, 旋转后坐标向量为X2,则X1 = Ry(θ) * X2。
3)第三步是绕机体坐标系的X轴逆时针旋转,得到翻滚角Roll,大小为Φ,旋转矩阵为(这里是从机体坐标系变为地理坐标系的反向旋转矩阵):
假设旋转前向量为X2, 旋转后坐标向量为X3,则X2 = Rx(Φ) * X3
4)假设旋转前向量为X0,经过三次旋转后的向量变为X3,则由X3变换到X0的步骤为:
X0=Rz(Ψ) * Ry(θ) * Rx(Φ) * X3
那么此时的从机体坐标系到地理坐标系的旋转矩阵为:
R = Rz(Ψ) * Ry(θ) * Rx(Φ)
这个姿态矩阵就是用三个欧拉角(偏航、俯仰、翻滚)来表示的,这个第一种表示方式。
方向余弦表示姿态矩阵:
以下来自Starlino_DCM_Tutorial.pdf这篇文章,原文:http://www.starlino.com/dcm_tutorial.html,本文参考:https://www.cnblogs.com/andychenforever/p/6298073.html。
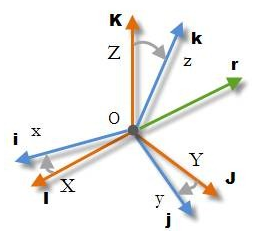
我们将本体坐标系定义为O-xyz,另外一个全局坐标系定义为O-XYZ,两坐标系的具有相同的原点O,如图所示。本体坐标系的x、y、z轴对应的单位向量分别为i,j,k;全局坐标系X、Y、Z轴对应的单位向量分别为I,J,K。
这就是用方向余弦表示姿态矩阵,这是第二种表示方式。
四元数表示姿态矩阵:
以下来自秦永元的《惯性导航》。
四元数介绍:
四元数表示姿态矩阵:
一个坐标系到另一个坐标系的旋转,除了可以分解为绕坐标系中的Z轴、Y轴、X轴旋转三次得到外,旋转的一个神奇之处就在于,三维空间的任意旋转,都可以用绕三维空间的某个轴旋转过某个角度来表示,即所谓的Axis-Angle表示方法。这种表示方法里,Axis可用一个三维向量(x,y,z)来表示,θ可以用一个角度值来表示,直观来讲,一个四维向量(θ,x,y,z)就可以表示出三维空间任意的旋转。注意,这里的三维向量(x,y,z)只是用来表示axis的方向朝向,因此更紧凑的表示方式是用一个单位向量来表示方向axis,而用该三维向量的长度来表示角度值θ。这样以来,可以用一个三维向量(θ*x, θ*y, θ*z)就可以表示出三维空间任意的旋转,前提是其中(x,y,z)是单位向量。这就是旋转向量(Rotation Vector)的表示方式。
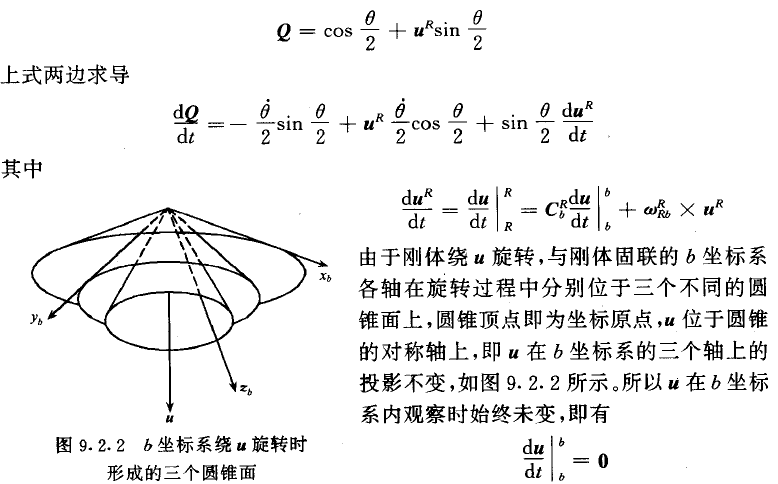
Axis-Angle的表示方法还可以推导出另一种很常用的三维旋转表示方法,叫四元数(Quaternion),具体的证明参考秦永元的《惯性导航》。同上,假设(x,y,z)是axis方向的单位向量,θ是绕axis转过的角度,那么四元数可以表示为[cos(θ/2), x*sin(θ/2), y*sin(θ/2), z*sin(θ/2)]。注意,这里可以推导出,用于表示旋转的四元数向量也必须是单位向量。四元数的神奇之处在于,对于三维坐标的旋转,可以通过四元数乘法直接操作,与上述旋转矩阵操作可以等价,但是表示方式更加紧凑,计算量也可以小一些。捷联惯导中的姿态更新实质上是如何计算四元数Q。
其中R代表地理坐标系,b代表机体坐标系,u是R系中一个旋转向量(单位向量),机体绕着这个旋转向量旋转,θ表示转过的角度。
这就是用四元数表示姿态矩阵,这是第三种表示方式。
欧拉角、方向余弦、四元数之间的关系:
这里的四元数q0=a,q1=b,q2=c,q3=d,三者关系为:
通过比较上述等式的各个元素,四元数可以直接用欧拉角或余弦表示,同样欧拉角也可用方向余弦或四元数表示。
1)用方向余弦表示四元数:
2)用欧拉角直接表示四元数:
3)用方向余弦表示欧拉角:
上面这些就是姿态解算用到的四元数及四元数求解欧拉角的方法了。基本思路是四元数—>方向余弦—>欧拉角。这样就又有问题了四元数的q0-q3数据来源是什么呢?又是如何填充q0-q3呢?
上边我们介绍了姿态矩阵有三种表示方式,分别是欧拉角、方向余弦、四元数,这一节我们来说说姿态矩阵的的更新。
欧拉角的优缺点:
优点:
我们说过,用欧拉角表示方向(或者说,方向变换)只需要用到三个参数,即三个旋转角度(因为坐标轴是旋转轴,所以不用增加特别的参数描述旋转轴),这样做有一个非常大的优点,就是表述清晰易懂。
缺点:
1)歧义问题。简单来说就是,当给定了欧拉角以后,我们很容易找到欧拉角表述的方向,但是当我们获得了一个方向以后,却不一定能求出它旋转的欧拉角。原因很简单,三维空间中的任意一个方向都可以通过至少两种不同欧拉角表示。比如,同样的yaw-pitch-roll顺序,(0,90,0)和(90,90,90)会将刚体转到相同的位置。
2)欧拉角可能造成万向节死锁的问题,而要规避万向节死锁,需要选择合适的旋转顺序(有12种旋转顺序)
3)欧拉角的插值比较难。
因此,直接使用欧拉角的情况比较少。在此不介绍欧拉角的姿态矩阵跟新。
方向余弦所表示的姿态矩阵更新:
仅仅考虑刚体转动,由动力学知识可知,对于任意向量 求导(类比圆周运动v=rw):
其中e表示向量相对于地理(earth)坐标系,b表示相对于机体(body)坐标系,X 表示向量叉乘。
对于旋转矩阵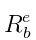

其中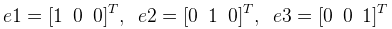
由

四元数所表示的姿态矩阵更新:
1、哥式定理:
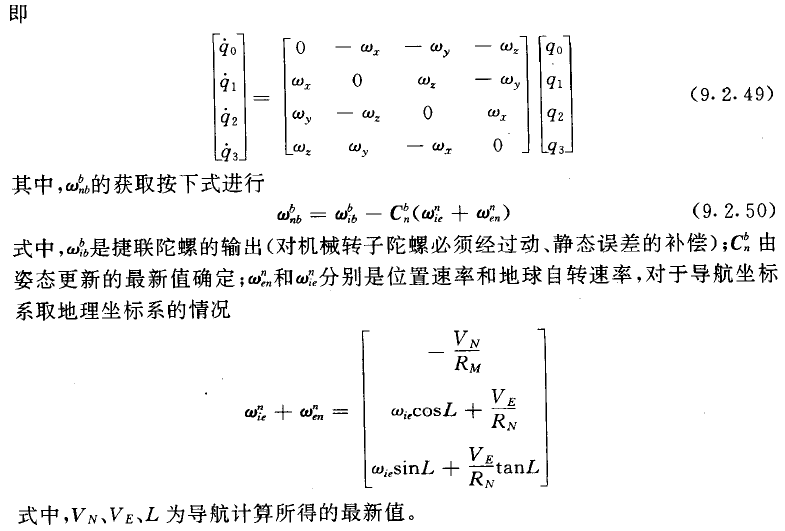
2、姿态矩阵更新:
在上一节中我们提到,表征b系到n系的四元数为:
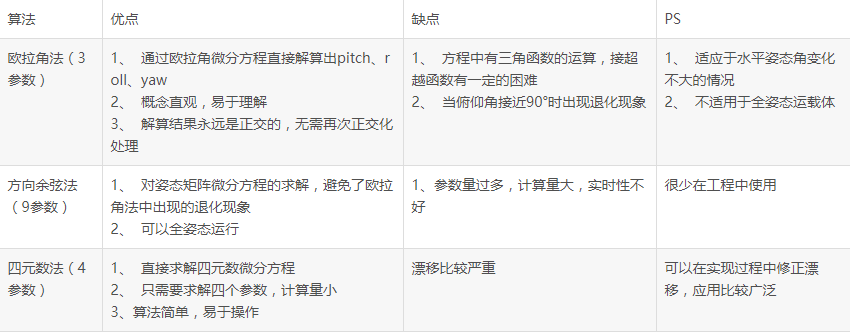
三种算法比较:
在姿态解算过程中,到底用什么表示无人机的姿态呢?姿态表示的方法有很多种,比如欧拉角、四元数、DCM,各有的各的优势,比较常用的就是四元数,方便计算。下面介绍一个它们三个的优缺点。