这篇文章从期末前写到期末后，因为内容实在太多了...这篇论文包含了深度学习中比较常见的几个概念，但因为我主要方向是图像领域，因此只对前半部分进行了学习。最近同时在看李宏毅老师的课程，没有专门记笔记，但是把一些内容融合在了下面概念的理解中。

论文阅读：Deep learning—Yann LeCun, Yoshua Bengio & Geoffrey Hinton

这是一篇概述性论文，作为深度学习论文学习的入门篇，作者是非常有名的几位老师。借这样一篇文章来学习几个基本概念：深度学习，监督学习，反向传播和卷积神经网络等。

深度学习(Deep learning)

在一些机器学习的应用领域中，比如确认图片中的物体，将语音转化为文本，根据用户兴趣为其匹配产品等，深度学习的使用越来越多。因为在这些领域中，传统的机器学习方法面临一些问题：

传统的机器学习方法处理原始形式数据的能力有限，它们需要人为地将数据转化为分类器可以处理的形式，这其中包括对特征进行筛选等特征工程。由于应用领域的不同，特征工程会需要该领域的专业知识对特征进行处理，有一定的门槛；尤其是对于大量数据，手动特征工程的效率和效果都不理想；
传统的机器学习方法的表示能力(representation ability)有限。相比之下，深度学习是将多个具有表示(representation)能力的模块(module)叠加，可以得到不同水平的representation，逐步地将原始数据表示成更抽象，复杂的形式。
在某些领域，需要对数据的一部分特性具有强选择性，保留了强分辨能力；另一方面模型需要对数据的一部分具有鲁棒性，即不受该部分数据干扰，比如背景，光照等等。这种强建模能力需要通过深度学习来实现。(也就是深度学习会具有平移不变等特性)

监督学习(Supervised learning)

监督学习是最常见的机器学习模式。监督学习中必须要有标记好的训练数据，也就是标签(label)。训练前，模型并不知道正确的建模方向(参数未知，需要随机初始化)。在训练过程中，模型被给予数据和正确的结果，模型的建模能力可以将模型根据数据输出的结果与正确的标记结果进行对比得知。为了具体化这个建模能力，可以求两个结果间的差值，差值小，则表示建模是更向正确方向靠近的。为了提高模型的建模能力，需要不断调整参数以使差值最小。
损失函数(loss function)/目标函数(object function)
定义一个包含上述差值的函数，那么提高建模能力这个目标就可以转化为最小化这个函数，因此可以称为目标函数(对于一批数据，目标函数应该是这批数据的损失和或均值)；这个函数表示的是建模结果和正确结果间的差值，也就是误差/损失，因此又可以成为损失函数。
参数
参数指的是模型中一些需要设定的系数，这些系数决定了模型的建模方向。这些参数会出现在损失函数中，因此上述的最小化损失函数的具体措施就是调整这些参数，使损失函数取到局部最小值。
梯度下降
找到参数使得包含参数的函数尽快地取得最小值，就会涉及到求梯度，当然该梯度是损失函数对于参数的梯度。梯度表示了该损失函数在参数微微变化时的变化剧烈程度，对其取负值，就是最快的下降方向。那么参数就要沿该方向以一定的步长变化，使得损失函数迅速减小。不断地更新参数，直到损失函数不会再下降。
随机梯度下降：每次从训练数据中随机抽取一部分数据作为一个小集合来训练模型，也就是利用这些数据的模型输出结果和它们的正确结果构建损失函数，然后通过梯度下降的方法更新模型的参数，然后再次从训练数据中获取另一个小集合接着训练，直到损失函数取到最小。由于每次用来训练模型的都只是整体训练数据中的一小部分，损失函数和参数都是具有一定的噪声/偏差。但这种方法非常有效而且迅速。

反向传播(Back propagation)

深度学习是一层层模型叠加的，其实就是一层层神经网络叠加，所以参数其实是分布在不同层的。由于层与层之间是递进的关系(上一层的输出作为下一层的输入，因此有时序关系)，不同层的参数是不可能同时更新的，而是从整个深度学习的模型(事实上就是神经网络)的输出反向向输入一层层更新。每一层的更新都是上文提到的损失函数求梯度然后更新参数的过程。不过对于中间的层，如何得到损失函数对这一层参数的梯度呢？因为这一层的输出是一个中间值，在整个模型中是不会输出的，但这个中间值会通过下一层的参数继续影响后续的网络层，直到整个网络的输出。根据链式求导的原理，其实就是复合函数求导，我们可以根据最外层的结果来一层层向内求导得到输出对里层参数的导数。这个一层层求导的过程就利用了反向传播，把每一层参数的变化方向传递给该层，然后该层参数进行更新。所有层的参数完成一次更新后，整个网络才完成一次更新。
反向传播的理论基础是链式求导，根据具体的神经网络模型我们来推导反向传播的基本形式。

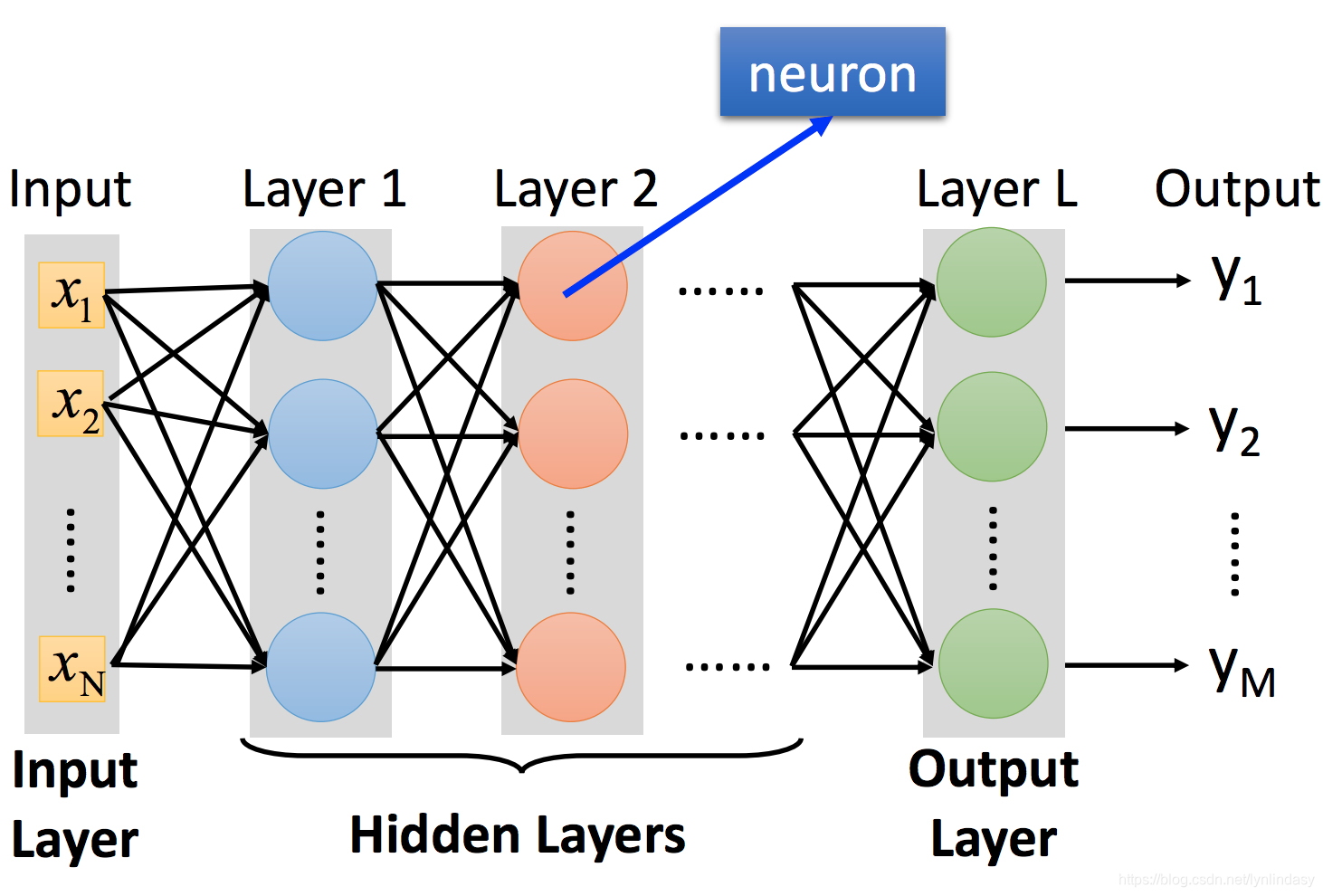
上图为一个简单的神经网络，输入用向量x表示，输出用向量y表示，中间是一层层堆叠的隐藏层。输入x会经过一个线性组合也就是图中的箭头(可以表示为矩阵相乘)得到Wx，在加上偏置向量b得到图中Layer 1的输入 $z^{(1)}=W^{(1)}x+b^{(1)}$ ，这里所有变量和参数的上标1均表示神经网络中的第一层隐藏层(输入层其实可以视为第零层也就是 $x=z^{(0)}$ )，第一层中的神经元也就是图中蓝色的圆圈会对这个输入进行非线性操作，也称作激活(activation)，我们用式子 $a^{(1)}=\sigma (z^{(1)})$ 表示， $a^{(1)}$ 就表示activation后的结果也就是这层网络的输出，后面的每一层网络都进行上述的操作，直到输出层也就是第L层 $a^{(L)}$ 就是输出向量y。这就是神经网络的前向计算过程(forwad pass)。

整个网络的流程可以表示为 $y=\sigma (W^{(L)}(\sigma (W^{(L-1)}(...\sigma (W^{(1)}x+b^{(1)})...)+b^{(L-1)}))+b^{(L)})$ 。

网络的loss function我们定义为 $L=\frac{1}{2m}\sum_{i=1}^{M}(\hat{y_{i}}-y_{i})^{2}$ ，这只是其中一种形式，也可以定义为交叉熵形式等，其中 $\hat{y}$ 为数据的标签(label)。为了简化推导过程，loss function简单定义为 $L=\frac{1}{2}(\hat{y_{i}}-y_{i})^{2}$ ，即不对数据的总loss取平均。

接下来就是利用grandient descent的方法更新参数，可知想要更新参数 $W^{(1)}$ ， $b^{(1)}$ ...就需要求得 $\frac{\partial L}{\partial W_{i,j}^{(1)}}$ ， $\frac{\partial L}{\partial b_{i}^{(1)}}$ ...这些偏导数需要通过链式法则求得。

对于权重W，有 $\frac{\partial L}{\partial W}=\frac{\partial L}{\partial y}\frac{\partial y}{\partial W}=\left (y-\hat{y} \right )\frac{\partial y}{\partial W}$

对于第L层， $y=\sigma (W^{(L)}a^{(L-1)}+b^{(L)})$ ，则

$\frac{\partial y}{\partial W^{(L)}}={\sigma }'(W^{(L)}a^{(L-1)}+b^{(L)})a^{(L-1)}$ ，其中

${\sigma }'(W^{(L)}a^{(L-1)}+b^{(L)})={\sigma }'(z^{(L)})$ 是一个常数， $a^{(L-1)}$ 也是在前向计算时可以得到的常数(是第L层神经网络的输入(第L-1层神经网络的输出))。

对于第L-1层， $y=\sigma (W^{(L)}a^{(L-1)}+b^{(L)})=\sigma (W^{(L)}(\sigma (W^{(L-1)}a^{(L-2)}+b^{(L-1)}))+b^{(L)})$ ，则

$\frac{\partial y}{\partial W^{(L-1)}}=$ ${\sigma }'(W^{(L)}(\sigma (W^{(L-1)}a^{(L-2)}+b^{(L-1)})+b^{(L)})W^{(L)}{\sigma }'(W^{(L-1)}a^{(L-2)}+b^{(L-1)})a^{(L-2)}$

$={\sigma }'(z^{(L)})W^{(L)}{\sigma }'(z^{(L-1)})a^{(L-2)}$ $={\sigma }'(z^{(L)}){\sigma }'(z^{(L-1)})W^{(L)}a^{(L-2)}$

定义 $\delta ^{(L)}=(y-\hat{y})\sigma '(z^{(L)})$ 表示输出层每个节点的误差， $\delta ^{(i)}=\delta ^{(i+1)}\sigma '(z^{(i)})W^{(i+1)}$ 表示第i层每个节点的误差，那么

$\frac{\partial L}{\partial W^{(L)}}=(y-\hat{y}){\sigma }'(z^{(L)})a^{(L-1)}=\delta ^{(L)}a^{(L-1)}$ ，

$\frac{\partial L}{\partial W^{(L-1)}}=(y-\hat{y}){\sigma }'(z^{(L)}){\sigma }'(z^{(L-1)})W^{(L)}a^{(L-2)}$

$=\delta ^{(L)}{\sigma }'(z^{(L-1)})W^{(L)}a^{(L-2)}=\delta ^{(L-1)}a^{(L-2)}$

$\frac{\partial L}{\partial W^{(i)}}=\delta ^{(i)}a^{(i-1)}$

到这里已经可以看出对每一层求偏导的过程都在从输出层反向传递误差，权重W的更新公式为 $W^{(i)}=W^{(i)}-\eta \frac{\partial L}{\partial W^{(i)}}$ ， $\eta$ 为步长。

类似地，对于偏差b，有 $\frac{\partial L}{\partial b}=\frac{\partial L}{\partial y}\frac{\partial y}{\partial b}=\left (y-\hat{y} \right )\frac{\partial y}{\partial b}$

对于第L层，则有 $\frac{\partial y}{\partial b^{(L)}}={\sigma }'(W^{(L)}a^{(L-1)}+b^{(L)})$ ，与W相比，其实只少了一项 $a^{(L-1)}$ 。因此

$\frac{\partial L}{\partial b^{(L)}}=(y-\hat{y}){\sigma }'(z^{(L)})=\delta ^{(L)}$ ， $\frac{\partial L}{\partial b^{(L-1)}}=\delta ^{(L-1)}$ ， $\frac{\partial L}{\partial b^{(i)}}=\delta ^{(i)}$ ，偏差b的更新公式为 $b^{(i)}=b^{(i)}-\eta \frac{\partial L}{\partial b^{(i)}}$ 。

以上就是反向传播法(back propabation)实现的梯度下降。在这里只是简单推导了公式，应用中图像基本都是矩阵和向量，更详细的推导可以参考这篇文章：https://mp.weixin.qq.com/s?__biz=MzU4MjQ3MDkwNA==&mid=2247485446&idx=1&sn=57d7d866443810c20c4ea2c6ee8018cc&chksm=fdb69591cac11c8773638b396abe43c0161e4d339f0fa845e54326be3e8c4933a3b6a2713dae&mpshare=1&scene=1&srcid=0115Lac63cKJ9TN4nJfSFBnK

参考李宏毅老师的课程，反向传播的过程完全可以看作是利用了一个反向的网络：

这个图中的C就是我们使用的loss function：L，图中的三角形就是 ${\sigma }'(z^{(i)})$ ，这个常数的作用就类似一个放大器。红色的箭头就是该层的权重W。

卷积神经网络(Convolutional neural network—CNN)

卷积神经网络的输入，输出，卷积核都是三维的，分别是高度(height)，宽度(width)，深度(depth)/通道(channel)。其中深度(depth)/通道(channel)的概念，对于网络的输入来讲，深度就是输入图片的RGB三个通道，随着卷积网络对图片的处理，深度会改变，也就不再表示RGB的意义。卷积神经网络一般会包括卷积层，池化层，全连接层等。

卷积层(Convolution Layer):

基本概念：

卷积(convolution)：卷积层做的是卷积的工作，卷积实际上可以理解为翻转，平移，相乘，累加的过程，但神经网络中的卷积没有翻转的过程。对图像进行卷积操作的是卷积核(kernel)，其实就是一个小掩模(mask)，一般有1*1，3*3，5*5或7*7大小。卷积核在卷积层的输入(可能是原始图片或者是特征图(feature map))的像素点上进行滑动。每滑动到一个像素点时，卷积核与输入特征图对应的区域进行element-wise product，然后累加求和得到一个值，作为输出feature map的一个元素。然后卷积核以一定的步长(stride)继续滑动。
卷积核(kernel)：卷积核的参数是卷积神经网络(CNN)中参数的主要来源，卷积核(kernel)的大小若是1*1，深度为128(后续可能表示为1*1*128)，则有参数1*1*128=128个。注：卷积核的深度是要与输入图像的深度相匹配的。例如，该层的输入图像如果是224*224*3的，那么卷积核的深度/通道数必须为3，这样每一通道的卷积核与对应的输入图像的该通道一一进行卷积操作，然后多个通道数的卷积结果相加得到一个深度为1的结果。
特征图(feature map)：卷积层可以从图像中提取特征(之后详解)，图像经过卷积层后会得到尺寸(可能)会减小的小图片，小图片的内容是一些图像的特征，比如纹理等，这个表示了原图像特征的小图片就是特征图(feature map)。特征图和原图像一样，一般具有三个维度，其中的深度(depth)/通道(channel)是由上一层中的卷积核(kernel)的个数决定的。注：通常每个卷积层并不是只有一个卷积核，每个卷积核卷积后只会产生一个特征图，m个卷积核就会产生m个特征图，也就是深度/通道数为m的特征图。如下图所示，CONV对应的图片就是特征图，不同层的特征图表征的特征也不同，从左至右特征是越来越抽象，越来越高级的，从边缘到轮廓到物体的一部分。

卷积的具体操作可以通过下面的图片理解：这个卷积中输入的图像是深度为3的7*7大小(7*7*3)，卷积核是深度为3的3*3(3*3*3)，一共有两个卷积核，因此输出是深度为2的3*3特征图。

池化层(Pooling Layer)：

池化一般有几种形式：最大池化(max pooling)，平均池化(average pooling)等。池化其实也可以看作一个卷积的过程，只不过这个卷积核上的参数改变了形式，直接成为了一个取最大值或平均值的函数，这其实就是一个下采样(subsampling)的过程。

如上图所示，池化就是把整张图片或者特征图划分为几个不相交的pool(区域)，每个pool中只取出一个值(最大值或者平均值等)。最常见的池化是2*2的，那么产生的结果就是图像尺寸会缩小为原来的一半。

注：卷积是会融合不同通道的信息的，一个卷积核会将自己的各个通道与特征图的各个通道对应，一一做卷积后结果相加，最后产生一个一层的特征图；池化不对深度这个维度进行融合操作，池化只停留在二维平面内。因此输入是m个通道的特征图，输出时仍然是m个通道，只不过宽高减半。

池化层一般接在卷积层后，但可能不是每一个卷积层后都会有池化。

全连接层(Fully Connected Layer)：

全连接层的内容几乎在前面讲解过了，这是最简单的网络模型。在CNN中，全连接层一般接在网络的最后面。卷积层和池化层的输入都是张量(Tensor)，也就是高维的matrix(因为图像有RGB三个通道，因此有深度信息，不仅仅是二维的)。但全连接层的输入是张量平铺(flatten)后得到的向量(vector)，是一维的。

在这样的flatten操作后，由于后续的全连接，相当于打乱了之前的局部连接。卷积操作是在整张图片中提取一个模式，而全连接则会把不同模式综合起来，是对一整张图片的大特征提取(后面详解)。

以上就是CNN基本的组成部分，一个简单的CNN架构就如下图所示：

CNN特性：

1. 局部连接(Local Connectivity)：局部连接是卷积层很重要的特性，“局部”是相对于全连接层而言的。全连接层是指每一层的每一个神经元都会与前一层的所有神经元相连，也就是上一层有m个神经元，该层有n个神经元，则其间就会有mn个连接。如下面左图和右图左侧所示。但卷积层是只与上一层局部的神经元连接，可以看到下面右图中黑色，红色，绿色，蓝色的神经元都只对应了图中的一部分。

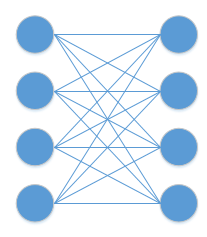
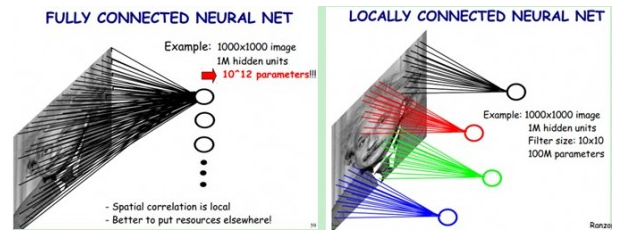
可以通过下面的图片理解卷积层的局部连接和卷积操作。

Image是5*5大小的，而右侧Convolved Feature也就是卷积后得到的特征图是3*3大小的。若是全连接，则特征图中的9个pixel每一个都会与Image中的5*5=25个pixel相连，参数共225个；但是卷积中，特征图的每个pixel只会与Image中的9个pixel相连(这里可以推断出卷积核应该是3*3的)，参数共9*9=81个。到这里应该可以明白，所谓的卷积核就是“连接”上的参数，卷积核的大小就是局部连接的范围(所以全连接其实可以视为是卷积核为原图大小的mask)，而结果的特征图中的每个pixel就是把卷积核上的参数作为权重，对Image实现了卷积核大小的局部连接。可以看到，局部连接使得参数个数减少了很多，局部连接也可以称为“稀疏连接”(Sparse connectivity)。

局部连接受启发于生物学，视觉皮层的神经元就是局部感知的。对应到图像中，可以理解为，只有近距离的pixel之间有较强的相关性，较远的部分并无关联，因此没必要进行全局感知。

2. 参数共享(Parameter Sharing)：参数共享其实就是之前卷积过程中卷积核的“滑动”。一个卷积核就代表了一组参数，共享是指卷积得到的特征图中的每个pixel都是通过同样的参数(同一个卷积核)对Image卷积操作后得到的。如上图，无论是特征图左上角的这个4，还是后面的其他pixel，都是用Image左上角黄色方框内的红色小数字卷积核得到的，这就是参数共享。一个卷积核的9个参数，对整张图片进行了卷积，因此产生这一个卷积核的参数不再是9*9=81，而是9*1=9。参数个数大幅下降。

参数共享用生物学理解，可以解释为相邻神经元特性接近，因此可以用相同的参数。对应到图像中：卷积操作可以看作是提取特征的过程，一个卷积核就对应了一种特征，通过其参数来实现对该特征的提取。而这个特征应该与其在图像中出现的位置无关，比如一个边缘，无论出现在图像的哪个位置，都应被提取到，因此对应该边缘的特征提取必须应用到整张图片上，这就实现了参数共享。

3. 池化(pooling)：池化的原理是图像下采样后只是分辨率下降，但不影响图象内容(object)。池化层函数实际上是一个统计函数。如果输入数据的维度大小为W×H，给定一个池化过滤器，其大小为w×h。池化函数考察的是在输入数据中，大小为w×h的子区域之内，所有元素具有的某一种特性。常见的统计特性包括最大值、均值、累加和及L2范数等。池化层函数力图用统计特性反应出来的1个值，来代替原来w×h的整个子区域。

池化相当于降低了分辨率，也就是图像会变得更模糊，但是其实并不会影响网络效果，是因为局部线性变换的不变性(invariant)：如果输入数据的局部进行了线性变换操作（如平移或旋转等），那么经过池化操作后，输出的结果并不会发生变化(池化相当于把像素平移)。

4. 多层次结构(many layers)：卷积层叠加后会逐渐提取出越来越高级和抽象的特征，使得网络的表示能力(特征提取能力)越来越强，效果也就越好。

李宏毅老师的课程中讲了一个非常有趣的方法，来理解各层网络实现的功能。

将CNN中第k个filter的输出中每个pixel写作 $a_{i,j}^{k}$ ，对整个特征图上的所有 $a_{i,j}^{k}$ 求和得到 $a^{k}$ ，表示的是这些神经元被激活的程度，值越大，表示激活程度强。接下来用梯度上升法求得使 $a^{k}$ 最大的输入图像x(这个x就是能让该特征图活性最强的图像，也就是与该filter/kernel所提取特征最匹配的图像)。这样通过x我们就能看出这个filter/kernel的作用是什么。

在中间的卷积层后取出的 $a_{i,j}^{k}$ 得到的结果如上图，对于每个filter找出了一张图片。可以看到，每张图片中都是遍布的重复的某种纹理。也就是说该filter提取的是这种纹理，当图片中全部是该纹理的时候，当然激活值是最大的。如果在后续的卷积层中提取 $a_{i,j}^{k}$ ，会发现它对应的输入图像中的内容应该是越来越抽象，越来越高级的特征。

当 $a_{i,j}^{k}$ 取自全连接层时，结果如下图：这时候不再是一张图片中包含重复的某种特征，而是有多种特征，综合到了一张图片里。说明此时全连接层的作用使得不同特征(也就是局部特征)融合，不再像卷积层只针对局部内容，全连接层已经开始对整张图片内容进行处理了。