Nuist集训队专题：数论

数论专题

前言
定理及公式补充
题A - Sum
题B - 2^x mod n = 1
题C - Dertouzos
结语

前言

本文所有内容均涉及以下主题：
在这里插入图片描述

定理及公式补充

1.取模运算基本公式
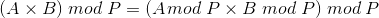
在这里插入图片描述
计算一个合数C%P，可以把C拆分为A*B，而C%P等价于A和B分别对P取模的积再对P取模。
百度百科—取模运算
2.费马小定理

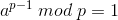
p是素数，对于任意整a，都有a的p-1次方对p取模结果为1.
百度百科—费马小定理
3.欧拉定理
只要a和m互质，就一定存在一个x，满足下式：
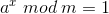
在这里插入图片描述
x为1到m中与m互质的数字的个数。
百度百科-欧拉定理

题A - Sum

链接：HDU-4704
在这里插入图片描述
大致描述一下这道题：
S(k)表示把N分成k(k<=N)份的方法数；
输入一个N，需要求出把N分别分成1到N份的方法总数对1e9+7取模的结果。

注意N的范围
N的范围达到了10^100000，远远超出64位长整数范围，所以选择用字符串读取。

如何表示S(k)并整理出一个通项公式？
此处采用组合数，把N分成k份相当于把N个苹果装进k个不同的篮子。当我们放完前k-1个盘子时，最后一个也就确定了，但是最后一个盘子至少要有1个苹果。
综上，所以我们得出组合数：
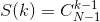
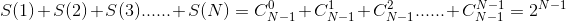
在这里插入图片描述

由此我们把该题转化成求2^N-1 mod 1e9+7

如何避免TLE？
本题给出的Time limit是1000ms，仅使用快速幂仍然会超时，此时，可以利用费马小定理。由于p=1e9+7是一个素数，所以我们可以把2^N-1拆解为2^(p-1)t+b，那么2^N-1等价于2^b对p取模，b是一个小于1e9+6的整数。

利用高精度数对低精度数取余求解b:

//pirme=1e9+7
//str[]为读取N的字符串
//len表示N的位数
long long MOD(long long len)
{
	long long b=0,i;
	for(i=0;i<len;++i)
		b=(b*10+str[i]-'0')%(prime-1);
	return b;
}

快速幂+取模的模板：

long long Qpow_mod(long long b)
{
	long long ans=1,n=2;
	while(b>0)
	{
		if(b&1)ans=ans*n%prime;
		n=n*n%prime;
		b>>=1;
	}
	return ans;
}

全代码：

#include<stdio.h>
#include<string.h>
long long prime=1e9+7;
char str[100001];
long long Qpow_mod(long long b)
{
	long long ans=1,n=2;
	while(b>0)
	{
		if(b&1)ans=ans*n%prime;
		n=n*n%prime;
		b>>=1;
	}
	return ans;
}
long long MOD(long long len)
{
	long long b=0,i;
	for(i=0;i<len;++i)
		b=(b*10+str[i]-'0')%(prime-1);
	return b;
}
int main()
{
	long long b,len;
	while(scanf("%s",&str)!=EOF)
	{
		len=strlen(str);
		b=MOD(len);
		printf("%lld\n",Qpow_mod(b-1));
	}
	return 0;
}

题B - 2^x mod n = 1

HUD-1395
此题可以直接循环暴力通过，以下暴力通过代码(／‵Д′)／~ ╧╧

#include<stdio.h>
int main()
{
	long long n,i,ans,ct=2;
	while(scanf("%lld",&n)!=EOF)
	{
		ct=2;
		if(n%2&&n!=1)
		{
			ans=1;
			do
			{
				ct=(ct*2)%n;
				++ans;
			}while(ct!=1);
			printf("2^%lld mod %lld = 1\n",ans,n);
		}
		else
			printf("2^? mod %lld = 1\n",n);
	}
	return 0;
}

2和所有除1以外的奇数互质，根据欧拉公式，只要2和n互质，那么就一定能解出x，满足表达式。

题C - Dertouzos

HDU-5750
这道题是要求:有多少个x，满足2<=x<=n，使得x除自身以外的最大因子是d.

怎样可以确认d是x除自身以外的最大因子
假设dr=x，首先要满足r<=d，其次考虑是否存在一个大于1的整数t，使得(dt)(r/t)=x，其中dt和r/t均为整数。如果存在，那么有dt>d，d就不是最大因子。所以r不能是一个合数，那么r就必须是一个质数。如此，这道问题就转化为求r的个数，r满足如下性质:

(1)r为素数；
(2)如果d为素数，那么r<=d;
(3)如果d为合数，k为d的最小素数因子，那么r<=k;
(4)dr<n;

经过初步思考，得出如下代码：

#include<stdio.h>
#include<math.h>
int main()
{
	long long T,n,d,i,j,flag,ct,p;
	while(scanf("%lld",&T)!=EOF)
	{
		while(T--)
		{
			ct=0;
			scanf("%lld %lld",&n,&d);
			for(i=2;i<=d;i++)
				if(d%i==0)
					break;
			p=i;
			for(i=2;i<=p;i++)
			{
				for(j=2;j<=sqrt(i);j++)
					if(i%j==0)
						break;
				if(j>sqrt(i)&&i*d<n)
					ct++;
			}
			printf("%lld\n",ct);
		}
	}
	return 0;
 }

以上代码运行的结果为标准结局(TLE)

问题出在处理素数太慢，由此可以得出，该题拐弯抹角就是让你做一个素数筛。
这道题n的范围达到1e9，所以埃氏筛很可能会导致标准结局++;
因此我们采用线性筛——欧拉筛法

以下欧拉筛模板:

bool flag[54000000];//标记是否为素数
int prime[54000000];//存储素数
void For_Prime()
{
	long long i,j,count=0;
	for(i=2;i<=54000000;++i)
	{
		if(!flag[i])
			prime[count++]=i;//如果没有被标记，该元素存入数组序列中
		for(j=2;j<count&&i*prime[j]<=54000000;++j)
		{
			flag[i*prime[j]]=true;//任意合数都能拆成一个素数乘一个整数，标记出这些合数
			if(i%prime[j]==0)break;//如果i模素数为0，说明接下去的标记都是重复运算，直接跳出循环
		}	
	}
}

完整AC代码:

#include<cstdio>
#include<iostream>
using namespace std;
bool flag[54000000];
int prime[54000000];
int count;
void For_Prime()
{
	long long i,j;
	for(i=2;i<=54000000;++i)
	{
		if(!flag[i])
			prime[count++]=i;
		for(j=0;j<count&&i*prime[j]<=54000000;++j)
		{
			flag[i*prime[j]]=true;
			if(i%prime[j]==0)break;
		}	
	}
}
int main()
{
	For_Prime();
	prime[0]=2;
	int T,n,d,i,ct;
	while(scanf("%d",&T)!=EOF)
	{
		while(T--)
		{
			scanf("%d %d",&n,&d);
			ct=0;
			for(i=0;i<count;++i)
			{
				if(prime[i]*d>=n||prime[i]>d)
					break;
				if(d%prime[i]==0)
				{
					++ct;
					break;
				}
				++ct;
			}
			printf("%d\n",ct);
		}
	}
	return 0;
}

~~在C语言中没有bool数组，所以用普通数组代替，而这样带来的结果就是MLE(标准结局2）。~~
(其实开字符数组也可以)

2018/12/05补充：
已知dr<n,r<=d，所以可以断言，如果d>sqrt(n)，那么我们实际上求得的r<n/d，所以在最坏情况下，r<=sqrt(n)，这意味着什么！我们的素数表打到31623(即sqrt(1e9)就够了，利用欧拉筛可以得知，小于31623的素数仅有3401个，我们的flag数组从原来的54000000变成了31623，prime数组从原来的54000000变成了3401，大大提高了运算速度，减少了内存。

原代码AC情况：
在这里插入图片描述
修改后AC情况：

以下贴出微调后的代码(纯C)：

#include<stdio.h>
char flag[31623];
int prime[3401];
int count;
void For_Prime()
{
	long long i,j;
	for(i=2;i<=31623;++i)
	{
		if(!flag[i])
			prime[count++]=i;
		for(j=0;j<count&&i*prime[j]<=31623;++j)
		{
			flag[i*prime[j]]='1';
			if(i%prime[j]==0)break;
		}	
	}
}
int main()
{
	For_Prime();
	prime[0]=2;
	int T,n,d,i,ct;
	while(scanf("%d",&T)!=EOF)
	{
		while(T--)
		{
			scanf("%d %d",&n,&d);
			ct=0;
			for(i=0;i<count;++i)
			{
				if(prime[i]*d>=n||prime[i]>d)
					break;
				if(d%prime[i]==0)
				{
					++ct;
					break;
				}
				++ct;
			}
			printf("%d\n",ct);
		}
	}
	return 0;
}

结语

前前后后肝了三天的题解，算是入门数论交的学费吧QAQ
有空补一下D题。
在这里插入图片描述
2018/12/04