哥伦比亚大学 NLP 第三章(第二部分)

哥伦比亚大学 NLP 第三章(第二部分)

目录

• 概率上下文无关
• $CKY$ 算法

本部分关于上下文无关相关符号的约定均基于第一部分，本部分将继续沿用不再定义
第三章第一部分传送门：https://blog.csdn.net/scanf_yourname/article/details/86777756

概率上下文无关文法 $(PCFGs)$

为什么引入概率上下文无关文法？

• 我们之前讲过与上下文无关文法，它的问题是会因为生成的分析树结构不同，也就是句式结构的不同引起歧义。
• 我们现在考虑一种方法解决这个问题，就是概率与上下文无关文法。在现实生活中，我们在面对一个歧义句的时候能够分辨那个是正确的语意，在很多情况下是因为有的句式结构下产生的句子是不符合逻辑的。所以，概率与上下文无关文法的目的就是为每一种可行的句式加上一个概率以判断什么是合理的句式结构。

定义概率上下文无关文法

• 概率上下文无关文法继承了上下文无关文法的四元组，在此基础之上 $PCFG$为 $R$中的每一个映射关系定义一个条件概率 $q(\beta_{j}|\alpha_{i})$，其中 $\alpha_{i}\epsilon V$， $\beta_{j}\epsilon \sum$， $\alpha_{i}\rightarrow\beta_{j}\epsilon R$。
  意味映射关系 $\alpha_{i}\rightarrow\beta_{j}$出现的概率为 $q(\beta_{j}|\alpha_{i})$
  规定： $\sum_{j=0}^{max} q(\beta_{j}|\alpha_{i})=1$
• 由于之前规定的左侧优先原则，我们便可根据上面的条件概率计算出每一种结构对应的概率，从而估计最可能结构。
  假设 $t$是一种可能存在的分析树结构，根据左侧优先原则，那么它的每一步映射都是确定的：
  $\alpha_{1}\rightarrow\beta_{1}$, $\alpha_{1}\rightarrow\beta_{1}......$ $\alpha_{n}\rightarrow\beta_{n}$
  则这颗分析树对应的概率 $P(t)=\prod_{i=1}^{n}q(\beta_{i}|\alpha_{i})$
  假设我们要列举所以可能的分析树比较他们的概率，这个所有生成树构成的集合是 $\tau(s)$, $T\epsilon\tau(s)$
  最终我们要求的就是所有可能分析树概率最大者：
  $arg max_{t\epsilon \tau(s) p(t)}$
  
  上图给出了求解右侧分析树概率的方法，按照树的先序遍历首先是 $S\rightarrow VP$,再依次是 $VP\rightarrow Verb$, $Verb\rightarrow Book.....$, $Noun\rightarrow fight$。我们就按照这个顺序将所有的概率乘到一起得到最后的概率。

如何通过数据学习一个 $PCFG$模型

• 数据来源： $Treebank$，分析树的数据，数据规模是 $50000$，数据是手工标记的分析树。 $40000$数据作为训练集， $2400$作为测试集，其他可能做交叉验证集了。
• 确定集合 $R$: $R$是所有训练集数据中涉及到的映射 $(\alpha \rightarrow \beta )$的集合。
• 确定 $q(\beta|\alpha):$这里采用似然估计用样本概率估计总体概率，公式如下：
  $q_{ML}(\beta|\alpha)=\frac{Count(\alpha \rightarrow \beta )}{Count(\alpha )}$

$CKY$ 算法

$CKY$ 算法是做什么的？

• 我们之前只是定义了一个分析树的概率大小，但是分析树的构建实际上是多种多样的，但是我们自然希望能够找到概率最大的那颗分析树，我们可以通过 $CKY$算法实现这一目的。

$CKY$ 算法的思想

• $CKY$是一个动态规划的算法，最终目标是求解 $max_{t\epsilon \tau(s)}p(t)$
• 首先是定义一些符号：
  $n=$句子中单词的个数
  $\omega_{i}=$句子中的第 $i$个单词
  $V=$句中非终结符的集合
  $S=$句子/分析树的开始符
  $\pi[i,j,X]$这是一个动态规划表，这个表中记录的是从单词 $\omega_{i}$到单词 $\omega_{j}$之间包含非终结符 $X$的概率最大值,其中 $i\epsilon[1,n],j\epsilon[1,n],i\leq j$且 $X\epsilon[\omega_{i},\omega_{j}]，X\epsilon V$
  比如： $\pi(2,5,NP)$代表的意思就是从第二个单词到第五个单词间包含非终结符 $NP$的最大概率。
  所有有了上述定义我们就把问题归结为求解 $\pi(1,n,S)$
• 初始条件：
  $\pi(i,i,X)=q(X\rightarrow \omega_{i})$ 其中 $(i\epsilon[i,n],X\epsilon N)$
  如果没有存在从 $X$直接或间接生成 $\omega_{i}$的文法那么 $q(X\rightarrow \omega_{i})=0$
• 状态转移方程：
  $\pi(i,j,X)=max_{X\rightarrow Y Z \epsilon R,s\epsilon[i...(j-1)]}(q(X\rightarrow YZ)*\pi(i,s,Y)*\pi(s+1,j,Z))$
  这个区间 $dp$感觉那状态转移方程描述好苍白啊，我觉得特别像最短路的迪杰斯特拉算法，同样是跑三层的循环，其中两层负责控制区间的两个端点 $i,j$，第三层负责在区间中间扫一遍，看看加入 $X$这个非终结符后，是否存在一个新的解析方法概率更大。
  
  上图是课件中的一个例子，我们现在要计算 $\pi(3,8,VP)$,如右侧所示 $VP$具有两种映射方式，我们依次对每一种映射方式重复下面的过程：对于一种映射关系，我们用变量 $s$遍历端点 $i,j$的每一种情况，如上图的前三行所示，实际上一共涉及五种情况。这样这两种映射关系实际上就一共有十种情况。这十种情况都是能够计算出一个具体的概率值的，而 $\pi(3,8,VP)$取他们中最大值

$CKY$算法的具体实现

• 输入：一个句子 $s=x_{1}...x_{n}$和一个概率上下文无关模型(包括那五元组)
• 初始化：
  $\pi(i,i,X)=q(X\rightarrow \omega_{i})$ $if$ $X\rightarrow \omega_{i}\epsilon R$
  $\pi(i,i,X)=0$ $otherwise$
• 算法实现过程
  
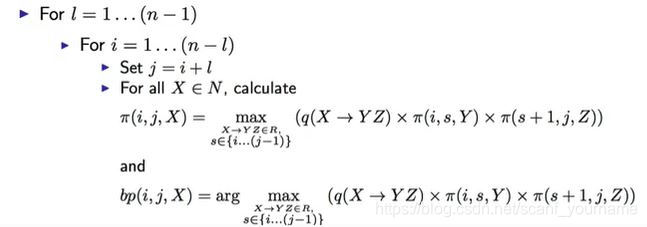
  循环的最外层是区间的长度由 $1$到 $n-1$,在长度确定的条件下不断更改区间的端点并通过状态转移方程更新 $\pi$的值。这里需要注意的是在更新 $\pi$值的同时不要忘了更新它对应的分析树，因为最后我们要得到的不是最大值，而是其对用的分析树结构。