梯度更新

举例说明

对于逻辑归回梯度求解：

假设预测输出函数：

$h (x_{0}, x_{1}, . . ., x_{n}) = \sum_{i = 0}^{n} θ_{i} x_{i} + θ_{0}$ $h(x_0, x_1,...,x_n)=\sum_{i=0}^n \theta_i x_i+\theta_0$

i：一次输入中，第i个数据
实际输出： $y$
Cost Function函数：
$J (θ_{0}, θ_{1}, . . ., θ_{n}) = \frac{1}{m} \sum_{j = 0}^{m} (y^{(j)} - h^{(j)})^{2}$ $J(\theta_0,\theta_1,...,\theta_n)={1\over m}\sum_{j=0}^m(y^{(j)}-h^{(j)})^2$

j：第j个输入，总共输入m个数据
梯度求解的最终目的：令 $J$ 的值最小，根据微积分，只要求出 $J'={dJ \over d\theta }={\partial J \over \partial\theta_i} \rightarrow 0$

根据导数的定义： $J=J-J'$ ， $J$ 肯定是往函数最小值方向移动，即 $J'\rightarrow 0或J\rightarrow \min$
但是通常情况下，由于 $J$ 很难直接求解出来，换个思路就是通过更新参数 $\theta_i^{(j)}$ 来实现： $J'\rightarrow 0或J\rightarrow \min$
- 如何保证参数 $\theta_i$ 更新方向是 $J\rightarrow \min$ ？
  
  求解：
  $θ_{i}^{+} = θ_{i} - Δ θ_{i}$ $\theta_i^+=\theta_i-\Delta \theta_i$ 根据导数定义，如果保证 $\Delta \theta_i$ 和偏导数 $\partial J \over \partial \theta_i$ 数值正负号一致，上述参数 $\theta_i$ 更新后， $J\rightarrow \min$
- 如何确定每次参数要更新多少？
  
  对于参数更新公式：
  $θ_{i}^{+} = θ_{i} - Δ θ_{i}$ $\theta_i^+=\theta_i-\Delta \theta_i$ 只是保证了参数更新方向正确，为了防止一步跨度太大，最终 $J$ 的值一下子垮过min，从而造成抖动，需要引入学习效率 $\eta$ ，最终公式： $θ_{i}^{+} = θ_{i} - η Δ θ_{i}$ $\theta_i^+=\theta_i-\eta\Delta \theta_i$
  
  一般: $\eta \in [0,1]$
小结：
$θ_{i}^{+} = θ_{i} - η Δ θ_{i}$ $\theta_i^+=\theta_i-\eta\Delta \theta_i$ 该公式属于人造并非数学推导，主要是符合了参数更新方向、同时人为设定更新步长

PS：某个权重更新的值=0，即 ${\partial J \over \partial \theta_i}=0$ ，并不代表 ${dJ \over d\theta}=0$

常见梯度更新方法

参考：http://blog.csdn.net/boon_228/article/details/51721835

BGD

批次梯度下降

概念：每次更新所有样本数据来更新一次 $J(\theta)$ 的参数 $\theta$
预测函数： $h (x_{0}, x_{1}, . . ., x_{n}) = \sum_{i = 0}^{n} θ_{i} x_{i} + θ_{0}$ $h(x_0, x_1,...,x_n)=\sum_{i=0}^n \theta_i x_i+\theta_0$
对于cost function： $J (θ_{0}, θ_{1}, . . ., θ_{n}) = \frac{1}{m} \sum_{j = 0}^{m} (y^{(j)} - h^{(j)})^{2}$ $J(\theta_0,\theta_1,...,\theta_n)={1\over m}\sum_{j=0}^m(y^{(j)}-h^{(j)})^2$
有参数更新公式： $θ_{i}^{+} = θ_{i} - η \frac{\partial J}{\partial θ_{i}} = θ_{i} - η \frac{2}{m} \sum_{j = 0}^{m} (y^{(j)} - h^{(j)}) x_{i}$ $\theta_i^+=\theta_i-\eta {\partial J \over \partial \theta_i}=\theta_i-\eta {2 \over m}\sum_{j=0}^m(y^{(j)}-h^{(j)})x_i$
这种参数更新方法是批量梯度更新，也就是每次更新 $\theta_i$ 都需要用到这样本里所有数据
小结：
- 优点：没更新一次，都用所有样本数据进行更新，这样就求解了全局最优解，同时通过计算公式可以发现可以并行实现；
- 缺点：由于每次更新都要计算该批次训练样本数据，如果批次样本数量太大，训练过程会很慢

SGD

随机梯度下降

概念：由于BGD每次更新都需要用到批次里所有样本数据，所以引入随机梯度下降概念；和BGD的区别在于，每次训练样本只输入一个，通过不断输入不同样本来修正参数，而BGD是一次输入所有样本来修正参数

区别	BGD	SGD
$h(x)$	$\sum_{i=0}^n \theta_i x_i+\theta_0$	$\sum_{i=0}^n \theta_i x_i+\theta_0$
$J(\theta)$	${1\over m}\sum_{j=0}^m(y^{(j)}-h^{(j)})^2$	${1\over 2}(y-h)^2$
每次输入样本数	所有	1个
循环次数	一次	=样本数量

小结：
- 优点：训练速度快；
- 缺点：准确度下降（噪音比BGD大），并非全局最优解；不易于并行实现；

MBGD

小批量梯度下降

概念：结合了BGD和SGD的优点：将所有的样本分割成很多小份，每次用这个小样本进行BGD训练，即：
```
for SGD:
    for BGD:
        ...
```
小结：
- 目前算法比较常用的梯度下降算法用MBGD，常用的小份样本数量有：64、10

常用梯度更新公式推导

神经网络常用梯度更新公式推导

Pooling

在池化层，设置了固定的w，所以参数不在此更新

主要类似设置了反向传播的阀门，保证反向阀门开合以及打开大小

这里的pooling方法是一般池化，即池化过程中，各个模块的边界不重叠。除了不重叠方法外，还有重叠池化、空金字塔池化

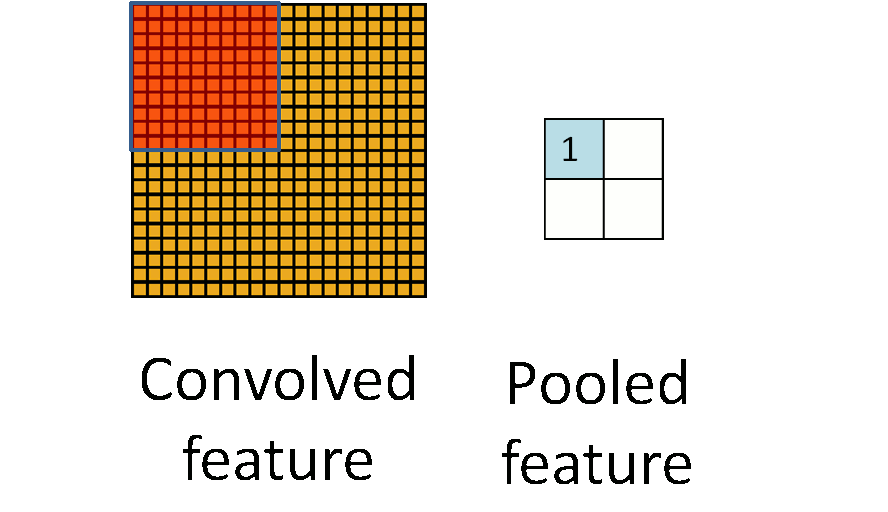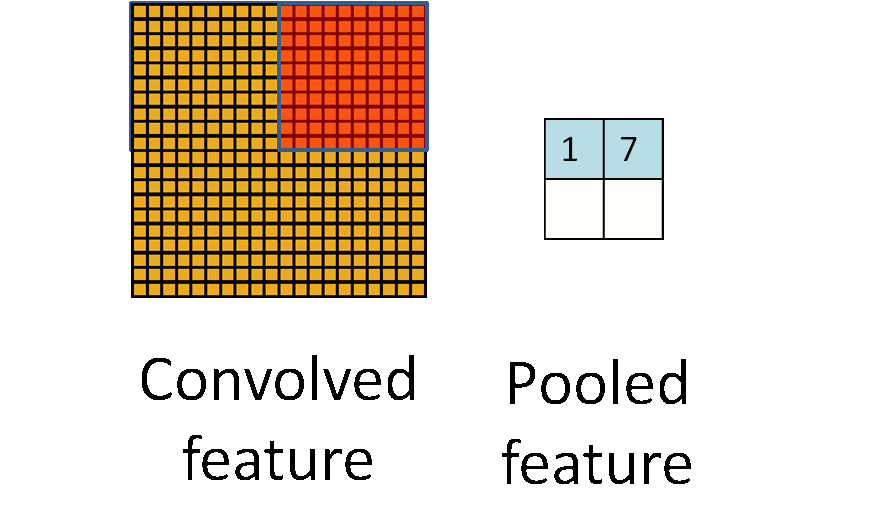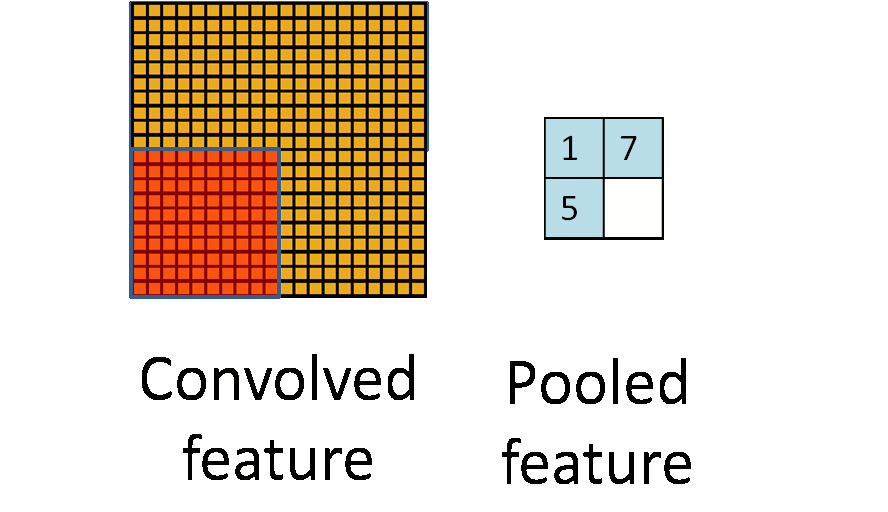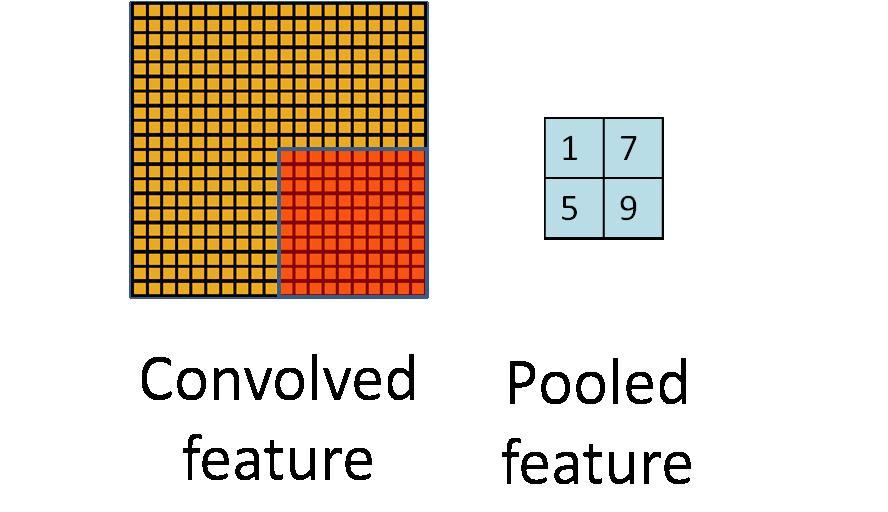
Max Pooling

概念：反向传播求导数过程类似分段函数求导

分段函数在分段点的导数必须分别求左右导数，而在非分段点的导数如常
有矩阵如下：

$\begin{matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{matrix}$ $\begin{matrix} 1&2&3\\ 4&5&6\\ 7&8&9\\ \end{matrix}$
求解整个矩阵的max_pooling，则：

$y = max (x_{1}, x_{2}, . . ., x_{9}) = 9$ $y=\max(x_1,x_2,...,x_9)=9$
反向传播时：

$\frac{\partial y}{\partial x_{n}} = {\begin{cases} 0, x_{n} 非最大值 \\ 1, x_{n} 是最大值 \end{cases}$

这个公式可以通过如下代码的条件语句实现：
```
if x_n == y:
    y_d = 1
else:
    y_d = 0
```
根据反向传播公式的链式原理：

$\begin{aligned} w^{+} & = w - η Δ w \\ = w - η \frac{\partial J}{\partial w} |_{x = x_{0}} \\ = w - η \frac{\partial J}{\partial O u t_{1}} \frac{\partial O u t 1}{\partial N e t_{1}} . . . \frac{\partial N e t_{i}}{\partial w} |_{x = x_{0}} \end{aligned}$ $\begin{align} w^+ &= w-\eta\Delta w \notag \\ &= w-\eta {\partial J \over \partial w}|_{x=x_0} \notag \\ &= w-\eta {\partial J \over \partial Out_1 }{\partial Out1 \over \partial Net_1}...{\partial Net_i \over \partial w}|_{x=x_0} \notag \\ \end{align}$

如果pooling层对 $x_i$ 偏导数为0，通过 $x_i$ 向前的参数修正值都恒为0，即不传播；
小结：
对于max pooling参数只通过max值那个点反向传播，在上述例子中，即通过 $x_9$ 向前修正参数，其他值均认为是无用数据丢弃；

Mean Pooling

概念：求解n x m矩阵的上所有点的均值
有矩阵如下：

$\begin{matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{matrix}$ $\begin{matrix} 1&2&3\\ 4&5&6\\ 7&8&9\\ \end{matrix}$
求解整个矩阵的mean pooling，则：
$y = \frac{(x_{1} + x_{2} + \dots + x_{n})}{n} = 5$ $y={(x_1+x_2+\cdots+x_n) \over n}=5$
反向传播时：
$\frac{\partial y}{\partial x_{n}} = \frac{1}{n} = \frac{1}{9}$ ${\partial y \over \partial x_n}={1 \over n}={1 \over 9}$
小结：
对于mean pooling ，反向传播过程中，只是给传播链条添加一个常数 $1 \over n$ ，即作为固定权重使用

激活函数

同Pooling，没有需要更新的权重，起到了传播过程中的阀门作用

ReLU

公式：
$y = {\begin{cases} 0, x \leq 0 \\ x, x > 0 \end{cases}$ $y=\begin{cases} 0, x \leq 0 \\ x, x > 0 \\ \end{cases}$
反向传播时：
$\frac{d y}{d x} = {\begin{cases} 0, x \leq 0 \\ 1, x > 0 \end{cases}$ ${d y \over d x}=\begin{cases} 0, x \leq 0 \\ 1, x > 0 \\ \end{cases}$
小结：
对于输出值： $x \leq 0$ 的神经元，流经ReLU层后的反向传播，该神经元以及前面对应的参数都会被丢弃，即不再更新参数

Sigmoid

公式：
$y = \frac{1}{1 + e^{- x}}$ $y={1 \over {1+e^{-x}}}$
反向传播时：
$\frac{d y}{d x} = y (1 - y)$ ${d y \over d x}=y(1-y)$

tanh

公式：
$y = \frac{e^{x} - e^{- x}}{e^{x} + e^{- x}}$ $y={e^x-e^{-x} \over e^x+e^{-x}}$
反向传播时：
$\frac{d y}{d x} = 2 (1 - y) (1 + y)$ ${dy \over dx}=2(1-y)(1+y)$

soft Max

公式：

$y_{i} = \frac{e^{x_{i}}}{\sum_{i = 0}^{n} e^{x_{i}}}$ $y_i={e^{x_i} \over \sum_{i=0}^n e^{x_i}}$

$x_i$ ：第i个输入值
$y_i$ ： $x_i$ 对应的输出值
反向传播时：
$\frac{\partial y_{i}}{\partial x_{i}} = y_{i} (1 - y_{i})$ ${\partial y_i \over \partial x_i}=y_i(1-y_i)$

Loss函数

交叉熵

理论上均方差 $C={(y-a)^2 \over n}$ 值小的程度，作为判断神经元预测结果和实际结果的偏离程度很好理解
但是，实际问题中，针对分类问题，交叉熵的表现比均方差来的好

设经过soft Max的神经元输出：
$\begin{array}{clll} 预测 z & 类别 1 (i = 1) & 类别 2 (i = 2) & 类别 3 (i = 3) \\ 样本 1 (k = 1) & 0.9 & 0.1 & 0.1 \\ 样本 2 (k = 2) & 0.1 & 0.9 & 0.1 \\ 样本 3 (k = 2) & 0.1 & 0.1 & 0.9 \end{array}$ $\begin{array}{c|lll} 预测z&类别1(i=1)&类别2(i=2)&类别3(i=3)\\ \hline 样本1(k=1)&0.9&0.1&0.1\\ 样本2(k=2)&0.1&0.9&0.1\\ 样本3(k=2)&0.1&0.1&0.9\\ \end{array}$
实际结果：
$\begin{array}{clll} 实际 y & 类别 1 (i = 1) & 类别 2 (i = 2) & 类别 3 (i = 3) \\ 样本 1 (k = 1) & 1 & 0 & 0 \\ 样本 2 (k = 2) & 0 & 1 & 0 \\ 样本 3 (k = 3) & 0 & 0 & 1 \end{array}$ $\begin{array}{c|lll} 实际y&类别1(i=1)&类别2(i=2)&类别3(i=3)\\ \hline 样本1(k=1)&1&0&0\\ 样本2(k=2)&0&1&0\\ 样本3(k=3)&0&0&1\\ \end{array}$
交叉熵公式：

$\begin{aligned} C_{k} = - \frac{1}{n} \sum_{i = 1}^{n} [y_{i}^{(k)} \ln z_{i}^{(k)} + (1 - y_{i}^{(k)}) \ln (1 - z_{i}^{(k)})], y_{i}^{(k)} \in {0, 1} \\ C_{1} \approx 0.035 \\ C_{2} \approx 0.035 \\ C_{3} \approx 0.035 \\ C = \frac{1}{m} \sum_{k = 1}^{m} (C_{k}) \approx 0.035 \end{aligned}$ $\begin{align} &C_k=-{1 \over n} \sum_{i=1}^n[y_i^{(k)} \ln z_i^{(k)}+(1-y_i^{(k)}) \ln (1-z_i^{(k)})], \ y_i^{(k)} \in \{0,1\} \notag \\ &C_1 \approx 0.035 \notag \\ &C_2 \approx 0.035 \notag \\ &C_3 \approx 0.035 \notag \\ &C={1 \over m}\sum_{k=1}^m(C_k) \approx 0.035 \notag \\ \end{align}$

$C_k$ ：第k个样本的交叉熵
$z_i$ ：某个样本的第i个类别预测结果
$y_i$ ：某个样本的第i个类别实际结果
反向传播时， $y_i$ 是已知值：
$\begin{aligned} \frac{\partial C}{\partial z_{i}} & = \frac{\partial C}{\partial C_{k}} \frac{\partial C_{k}}{z_{i}} \\ = \frac{1}{m} (- \frac{y_{i}^{(k)}}{n z_{i}^{(k)}}), y_{i}^{(k)} \in {0, 1} \end{aligned}$ $\begin{align} {\partial C \over \partial z_i}&={\partial C \over \partial C_k}{\partial C_k \over z_i} \notag \\ &={1 \over m}(-{y_i^{(k)} \over n z_i^{(k)}}), \ y_i^{(k)} \in \{0,1\} \notag \\ \end{align}$

梯度更新代码实现

TBD

梯度更新方法总结

梯度更新

举例说明

常见梯度更新方法

BGD

SGD

MBGD

常用梯度更新公式推导

Pooling

Max Pooling

Mean Pooling

激活函数

ReLU

Sigmoid

tanh

soft Max

Loss函数

交叉熵

梯度更新代码实现

猜你喜欢