文章转自: https://blog.csdn.net/zxm317122667/article/details/85159068
上一节我们讲了二叉树的定义,以及二叉树的遍历,这是面试中经常会问到的问题。但是坦白讲,在我们日常开发工作中普通的二叉树与二叉树遍历被用到的机会其实并不是很高。为什么这么说呢? 解答这道问题之前我们先来看一道面试题:
用一种数据结构将如下一组数据保存在内存中, 并提供元素查找操作
64, 50, 79, 10, 71, 30, 9, 88
假如我们使用完全二叉树来保存这组数据,则这棵树会是如下所示:
接下来在我们查找某数据元素的时候,就需要从根结点开始,使用二叉树的遍历方式,查找在这颗完全二叉树中是否存在这个数据元素。这样查找的时间复杂度为 O(N) , N为结点的个数。比如我们要查找的数据是88,那我们就需要遍历树中所有的元素并进行比较操作 64 -> 50 -> 79 -> 10 -> 71 -> 30 -> 9 -> 88。因为88是在树的最底层(叶子结点)
很明显这种存储方式并不是效率最高的。相反如果我们使用 HashTable 来存储这组数据到内存中的话,只要HashTable的哈希实现稍微合理,那在后续查找某一个数据元素时的时间复杂度甚至能达到 O(1),显然比二叉树快多了。
那二叉树岂不是没有可用之处??其实也不然,我们只要把上面的题目稍微改一下
用一种数据结构将如下一组数据保存在内存中, 并按照升序方式打印出所有数据元素
也就是说先将64, 50, 79, 10, 71, 30, 9, 88 保存在内存中,
然后按照从小到大的顺序打印出来 9, 10, 30, 50, 64, 71, 79, 88 。
这种情况,HashTable就显然不合适了,因为HashTable的存储是随机的。相反这时候用一种特殊形式的树形结构会效率更高,这种树形结构就是本节要讲的- -二叉搜索树
二叉搜索树(Binary Search Tree)
在计算机科学中,也被叫做有序二叉树。顾名思义,它被创建的目的就是为了实现快速查找操作。其实除了查询操作,二叉搜索树的插入和删除操作的效率也很快,并且使用二叉搜索树能够很方便的实现数据的排序遍历。而这些优势都取决于二叉搜索树的结构特点:
-
二叉搜索树中的任意结点,其左子树中的每个结点的值都小于这个结点的值
-
二叉搜索树中的任意结点,其右子树中的每个结点的值都大于这个结点的值
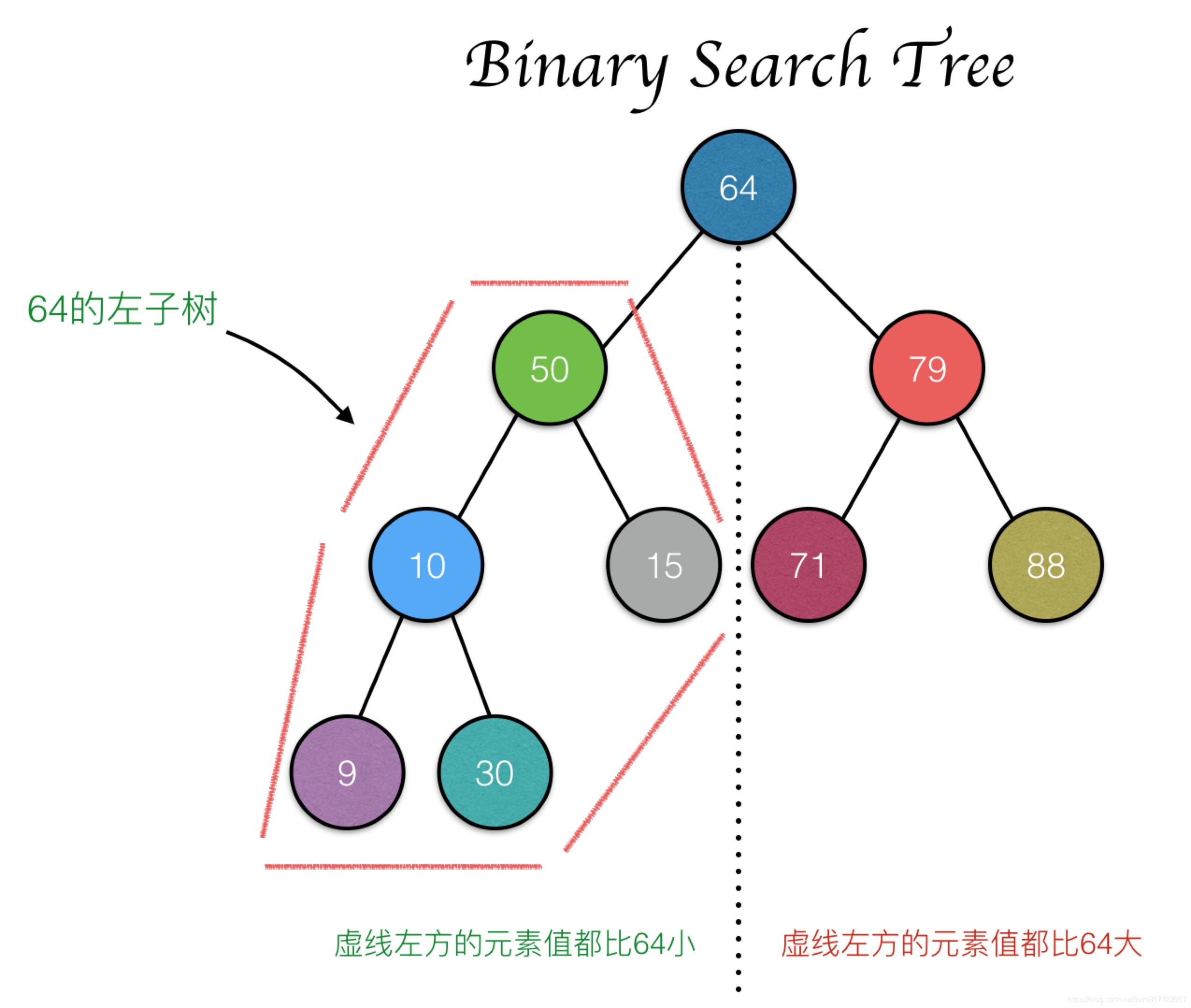
从图中可以看出,根结点64的左子树中(也就是虚线左半部分)的所有结点值都小于64。相反根结点20的右子树所有的结点值都大于64。
通过这样的结构,就不再需要遍历这组数据的所有元素。就如同 二叉搜索法 那样每经过一遍数据比较之后,都能够筛选掉近一半的元素。因此我们能很容易的猜出,二叉搜索树的查找操作的时间复杂度为 O(logN)。
这就比普通的完全二叉树的遍历操作快多啦 舒服!并且你猜怎么着?我们只需要在调用一下树的中序遍历就能把这一组数据按照从小到大的顺序给打印出来啦,是不是很奇妙。这就是二叉搜索树为什么这么受欢迎的原因
我们已经能够看出二叉搜索树既能实现快速查找,也能更好的实现排序效果,举个现实中的例子它就好比是一个各个语言都有涉猎的工程师,并且各种语言掌握的还不错。相反哈希表就是一个只专注于查找功能的工程师,对于Java技术甚至达到了精通的境界,但是其它语言可能很菜鸡
就个人而言,如果这两种只能做到其一,那我还是比较喜欢后一种,对于某一项语言达到高精尖的水平的工程师。因为当你对某一种语言达到这种理解之后,再看其它语言其实都是大同小异,学习起来也能举一反三了。
但是人类的欲望往往是很难满足的,就像地上有一张100美元和一张100人民币,那你是捡哪一张呢? 答案很明显:两种都要啊 哈哈!同样可不可以把二叉搜索树很HashTable的优点结合起来使用呢?答案也是肯定的–只要在HashTable基础上加上搜索二叉树的功能 -> HashMap就诞生了 。有兴趣的童鞋可以研究一下HashMap的源代码
二叉搜索树与哈希表的对比,可以参考下面几个链接
https://www.geeksforgeeks.org/advantages-of-bst-over-hash-table/
https://brackece.wordpress.com/2012/09/18/hash-table-vs-binary-search-tree/
https://stackoverflow.com/questions/4128546/advantages-of-binary-search-trees-over-hash-tables
二叉搜索树的操作
前面已经讲到,二叉搜索树支持快速查找、插入和删除操作。接下来我们看一下这三个操作是如何实现的。
对于二叉搜索树的查找操作,也就是在这颗二叉搜索树中查找某个结点。我们先取出根节点,如果它等于我们要查找的数据,那就返回。如果要查找的数据比根结点的值小,那就在左子树中递归查找,同样如果查找的数据比根结点的值大,那就在右子树中递归查找。
还是拿文章开始时的那组数据64, 50, 79, 10, 71, 30, 9, 88 举例。在基于这种规则的前提下,我们再去搜索88这个数据元素时,只要经过以下两部即可:
- 从根节点64开始,因为88 > 64,所以继续从根节点64的右子树中查找88
- 找到元素79,因为88 > 79,所以还是在结点79的右子树中查找88,从而找到元素88
上述流程可以参考如下GIF图: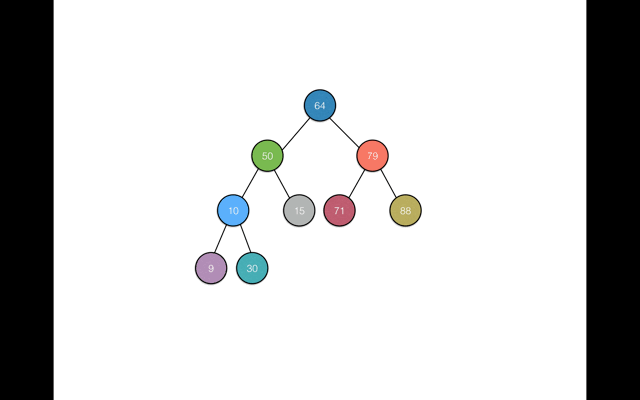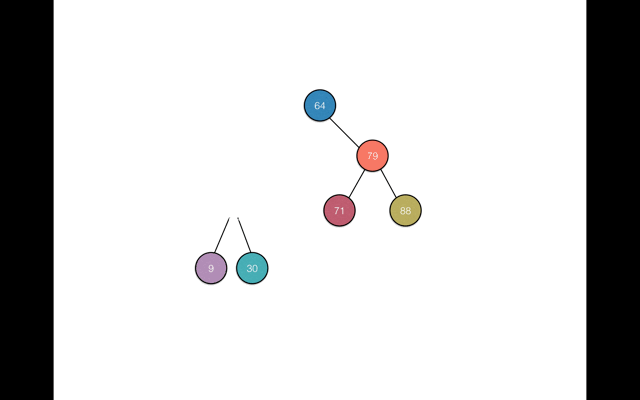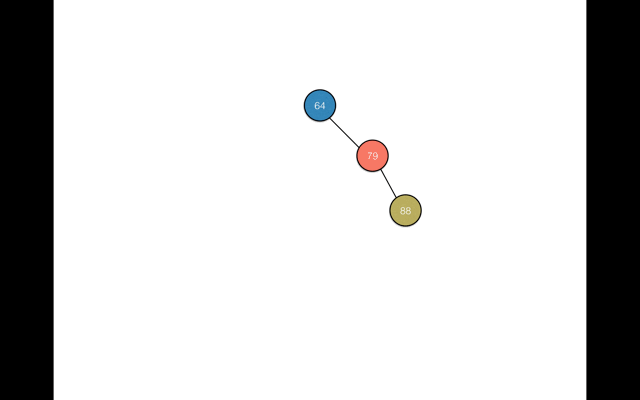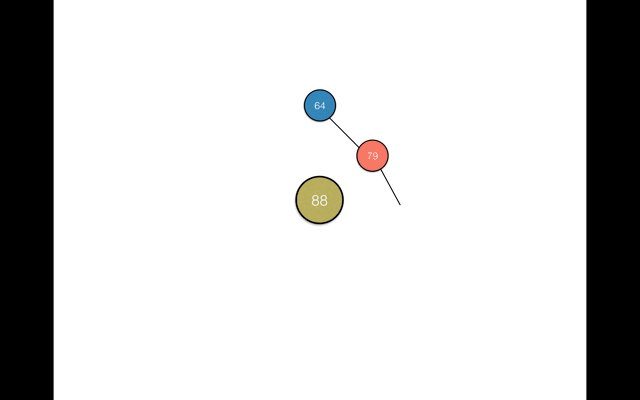
实现代码如下所示:
正如子曾曰过的: 有因必有果。二叉搜索树的查找操作之所以可以如此快速方便,就是因为在构建二叉树或者向二叉树插入数据时,也是按照同样的思路逻辑来处理数据的。
插入数据时,只需要从根结点开始,一次比较要插入的数据和结点大小的关系。如果要插入的数据比结点值大,并且右子结点为null,就将新数据直接插到右子结点的位置;如果不为null,就再递归遍历右子树,继续查找插入位置。同理,如果要插入的数据比结点值小,就在左子树中进行类似操作。
实现代码如下所示:
二叉树的查找、插入操作都比较容易理解,但是删除操作就相对比较复杂了。在讲解树形结构第一节的时候,我们就已经了解了树是一种connected的结构,也就是说结点与结点之间是连接起来的。那么问题就来了,如果我们将下面左边树中的10删除,那就会变成右图中的样子: 10的子树9和30没有父结点啦。成了没人管的小孩啦。
因此对于二叉搜索树中的删除操作,我们需要做的就是给失去父结点的子节点重新安排一个新的父结点。具体需要考虑的主要是以下几种情况:
1. 被删除的结点是叶子结点,也就是没有子结点。对于这种情况,我们只需要直接将父结点中,指向被删除结点的指针置为null即可
如下图中删除结点20,我们只需要将结点30的左指针置为null即可
2. 被删除结点只有一个子结点。这种情况我们只需要更新其父结点中指向被删除结点的指针,让它重新指向被删除结点的子结点就可以了
如下图中删除结点30,我们只需要将结点50的左指针置重新指向结点40
3. 最后一种情况就是要删除的结点有两个子结点。这种情况稍微复杂一点,首先需要找到这个结点的右子树中的最小结点Min,然后把它替换到被删除的结点上,然后递归的调用删除操作,删除这个最小结点Min
如下图中删除结点50,我们需要先找到结点50的右子树中的最小结点60, 并将50换成60的位置,然后将结点60删除
完整的删除操作实现代码如下:
二叉搜索树的缺点
在一般情况下二叉搜索树的插入,搜索,删除时间复杂度是O(logn),但是如果插入的数都是递增的话 如: (1,2,3,4,5,6,7,…)
这种情况构建出的二叉树如图所示:
这时的二叉搜索树就相当于一个单链表,插入,搜索,删除时间复杂度是O(n)
那么怎么解决这个问题呢:这问题的主要原因是数据偏向单边,使树的高度线性增长,为了能做到插入的数据不偏向单边,如果个节点的左子树高度与右子树高度相差<=1,那么就能做到插入,搜索,删除时间复杂度是O(logn),于是就有了 平衡 的概念,也就是我们下节要讲的 二叉平衡搜索树 。