机器学习 - 集成方法（Bagging VS. Boosting 以及随机森林、AdaBoost）

版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/weixin_37352167/article/details/84880590

• 集成方法

  集成（Ensemble）方法就是针对同一任务，将多个或多种分类器进行融合，从而提高整体模型的泛化能力。

  对于一个复杂任务，将多个模型进行适当地综合所得出的判断，通常要比任何一个单独模型的判读好。也就是我们常说的“三个臭皮匠，顶过诸葛亮”。

  不过对于组合分类器必须满足两点：

  (1) 基模型之间应该是相互独立的
  (2) 基模型应好于随机猜测模型

  集成方法目前分为两种：Bagging 与 Boosting，下面分别介绍。

• Bagging

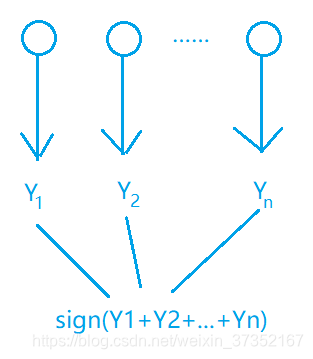
  Bagging（Bootstrap aggregating），又称装袋算法，它提供了一种非常直接的集成学习算法，即通过从完整数据集中抽取不同的子集喂给各个模型进行训练，最后将所有模型整合在一起，对被预测样本进行投票决定其所属类别。

  1. Bagging 分类：

     (1) 如果抽取的数据子集是从完整数据集抽取出的随机子集中再次抽取（先从完整数据集中抽取子集 A，再从子集 A 中抽取子集 B 作为训练集），成称为 Pasting

     (2) 如果从完整数据集抽取的子集是有放回的（每次抽取都是从相同的完整数据集中选取），称为 Boostrap

     (3) 如果抽取的数据集是特征的子集（n 个特征中挑出一部分特征，而样本数量与完整数据集相等），称为随机子空间 (Random Sub Spaces)

     (4) 如果同时对样本和特征都做抽取子集，称为随机补丁 (Random Patches)

     ---

     其中对于 Boostrap，最终完成样本抽样后有 36.8% 的数据未被抽到。计算方法：

     假设共有 n 个样本，每个样本不被抽到的概率为 $1-\frac{1}{n}$，

     抽取 n 次都不被抽到的概率为 $(1-\frac{1}{n})^n$，当 $n→+\infty$ 时，

     根据重要极限 $\mathop{}_{n→+\infty}^{\lim}(1+\frac{1}{n})^n=e$，

     求得： $\mathop{}_{n→+\infty}^{\lim} (1-\frac{1}{n})^n=\mathop{}_{n→+\infty}^{\lim}\frac{1}{(1+\frac{1}{-n})^{-n}}=\frac{1}{e}≈0.368$

  2. Bagging 的预测：

     (1) 对于分类任务，使用简单投票法，即每个分类器一票进行投票(也可以进行概率平均)；

     (2) 对于回归任务，采用简单平均获取最终结果，即取所有分类器的平均值；

  在 Bagging 方法中，所有的模型具有相同的权重，即 “完全民主决策”。

• Boosting

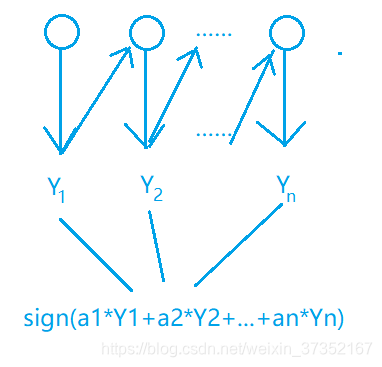
  提升（Boosting）方法，是通过改变训练样本的权重，学习多个模型，并将这些模型进行线性组合，从而提高性能。

  1. 两个定义

     $\bullet$ “强可学习”：对于一个任务，若存在一个多项式的学习算法能够学习它，且正确率很高，则称此学习算法为强可学习（Strongly Learnable）

     $\bullet$ “若可学习”：对于一个任务，若存在一个多项式的学习算法能够学习它，但正确率仅比随机猜测好，则称此学习算法为弱可学习（Weakly Learnable）

     对于这两个概念，后来证明，弱可学习与强可学习是等价的。如此，问题就转换成了：若一发现“弱学习算法”，那么能否将它提升为“强学习算法”。

     提升方法就是从弱学习算法出发，反复学习，得到一系列弱模型（基模型），然后组合这些弱模型构成一个强模型。

  2. 两个问题

     (1) 每一轮如何修改训练数据的权值（概率分布）

     答：提高上一轮预测错误的样本的权值，降低上一轮预测正确的样本的权值，如此，预测错误的样本会得到更大的关注。

     (2) 如何将弱模型组合成一个强模型

     答：使用加权多数表决。加大错误率小的弱模型的权值，减小错误率高的弱模型的权值，以此修改它们表决中产生的影响。

  Boosting 中，每个模型的权重不一样。

• Bagging VS. Boosting

  项目	Bagging	Boosting
  方法	① 训练只使用部分数据、特征；②多个模型多数表决	①训练基模型，而后学习上一轮的错误；② 多个模型线性加权
  流程	见图 - Bagging 流程	见图 - Boosting 流程
  偏 / 方差	主要降低方差，防止过拟合	主要降低偏差，提高准确度
  适用范围	高噪声	低噪声
  权重	所有训练数据权重相同，所有基模型权重相同	训练数据权重不同，每个基模型权重不同
  串 / 并行	并行（同时训练多个基模型）	串行（依赖上一轮模型结果）
  例	Random Forest	GBDT

（Bagging 流程图 ↓）

（Boosting 流程图 ↓）

• 随机森林

  随机森林是多棵决策树构成的，每一个棵树都根据自己“看到”的数据集进行训练，训练结束后对测试集进行各自的预测，并通过多数投票决策出最终的预测类别。

  对于“自己看到的数据”，便是通过 Bagging 的方式获得数据。使用 Boostrap、随机子空间等方法选出每个棵树各自使用的训练集。

• AdaBoost

  1. AdaBoost 算法过程

     这里通过 AdaBoost 方法介绍 Boosting.

     (1) 初始化训练数据的权值分布： $D_1=(W_{11},...,W_{1i},...,W_{1N})$， $D_m$ 代表第 $m$ 轮数据的权值分布。初始权值相等，为 $\frac{1}{N}$

     (2) 使用具有 $D_m$ 权重的训练数据进行学习，得到基模型： $G_m(x)$

     (3) 计算 $G_m(x)$ 在具有 $D_m$ 权重的训练数据上的错误率： $e_m=\sum_{i=1}^{N}W_{m,i}I(G_m(x)\neq y_i)$

     (4) 计算基模型 $G_m(x)$ 的权重系数： $α_m=\frac{1}{2}\ln \frac{1-e_m}{e_m}$

     (5) 更新训练数据集的权重分布： $D_{m+1}=(W_{m+1,1},...,W_{m+1,i},...,W_{m+1,N})$

     $W_{m+1,i}=\frac{W_{m,i}}{Z_m}e^{-α_my_iG_m(x_i)}$， $Z_m=\sum_{i=1}^{N}W_{m,i}e^{-α_my_iG_m(x_i)}$， $Z_m$ 为规范化因子，使得 $D_m(x)$ 成为概率分布

     (6) 构建基模型的线性组合，得到最终模型： $G(x)=sign(\sum_{m=1}^{M}α_mG_m(x))$

  2. 训练误差界

     这个点还没有吃透，后续添加。

  3. AdaBoost 算法的解释

     AdaBoost 算法可以被看做为：模型为加法模型，损失函数为指数函数，学习算法为前向分步算法时的学习方法。

     考虑加法模型： $f(x)=\sum_{m=1}^{M}β_mb(x;γ_m)$

     其中， $b(x;γ_m)$ 为基函数， $γ_m$ 代表基函数的所有参数， $β_m$ 为基函数的权重系数，显然 AdaBoost 是一个加法模型。

     对于学习加法模型 $f(x)$ 就成为经验损失极小化的问题： $\mathop{}_{β_m,γ_m}^{\max}\sum_{i=1}^{N}L(y_i,\sum_{m=1}^{M}β_mb(x;γ_m))$

     通常这是一个复杂优化的问题。前向分步算法求解此问题的思想是：因为学习的是加法模型，如果能从前向后，每步只学习一个基函数及其系数，逐步逼近优化目标函数，就可以简化优化的复杂度。

     由此，每步 只需要优化： $\mathop{}_{β,γ}^{\min}\sum_{i=1}^{N}L(y_i,βb(x;γ))$，相当于对于每步都求其最小化，那么最后结果也是最小的，蕴含着动态规划的思想。在分类问题中，AdaBoost 算法中的损失函数为指数函数： $L(y,f(x))=e^{-yf(x)}$.

参考文献
[1]: 集成算法中的Bagging