今天老师上课讲到了PageRank,因此查了一些资料
相关链接:
https://blog.csdn.net/guoziqing506/article/details/70702449
https://blog.csdn.net/rubinorth/article/details/52215036
http://www.cnblogs.com/rubinorth/p/5799848.html
https://www.changhai.org/articles/technology/misc/google_math.php
PageRank
随机游走模型
随机游走模型又称“醉汉模型”,指的是事物当前的状态只与其上一个状态有关,而与其再之前的状态无关。就好比一个醉汉,他这一步走到哪里只跟他上一步在哪里有关,这有点接近于物理学中常讲的“布朗运动”。
类比到网络浏览
我们可以假设,初始状态时,用户访问所有页面的概率都是等大的,而每次访问过后,用户会依照此时该页面中给出的链接以相等概率访问链接所指向的页面,那这就好比是用户在刚刚我们所说的有向图上做“随机游走”。所以,通过对这种随机游走的概率分析,我们就能得到用户在上网时,停留在哪一个网页上的概率要大一些,概率越大的,表示其质量越高。
数学化到PageRank
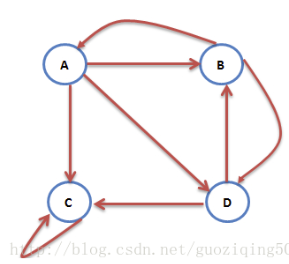
如果说最终的目的是要为每个网页赋予一个得分的话,那么在初始化阶段,所有网页的得分应该是相等的,假设现在一共有NN个网页,那么初始阶段用户访问每个网页的概率就是1N1N,比如下图中的初始概率向量为(1/4,1/4,1/4,1/4)(1/4,1/4,1/4,1/4),而因为每个网页都可能存在着到其他任何网页的链接,所以,我们可以将这些链接以平均的概率表示成一个概率转移向量。比如下面这张图,网页A中有3个链接,分别指向B, C, D,则A的概率转移向量为(0,1/3,1/3,1/3)(0,1/3,1/3,1/3),向量的维度依次对应的是网页A指向A, B, C, D四个网页的概率。

显然,每个网页都有这样一个概率转移向量,我们把这些向量转置后(按列放置)合起来就是随机过程中经典的概率转移矩阵了,如下:

不难理解,这种概率转移矩阵的一个显著的特征是每个元素都≥0≥0,且列和为1,含义表示从当前网页跳转到其他网页的概率和为1。我们记这个矩阵为TT,T[i][j]T[i][j]的含义是既可以表示由网页ii跳转至网页jj的概率,又可以表示由网页jj跳转至网页ii的概率。
根据这个矩阵,我们能够计算出经过一次网页跳转之后,用户访问到每个网页的概率分布,比如上图中,经过一次跳转之后,用户访问到各个网页的概率可以如下计算:
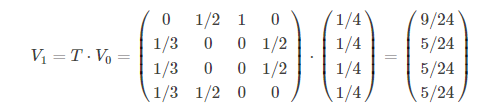
其中,T为概率转移矩阵。同理,我们可以按照这个方法持续计算到用户第n次跳转之后的概率分布,公式如下: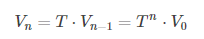
佩奇和布林发现,当n→+∞n→+∞,且概率转移矩阵TT满足以下3个条件时,limn→+∞Vnlimn→+∞Vn最终收敛,保持在一个稳定值附近。
- TT为随机矩阵。
即所有T[i][j]≥0T[i][j]≥0,且的所有列向量的元素加和为1,∑ni=1T[i][j]=1∑i=1nT[i][j]=1 - TT是不可约的。
所谓不可约是说TT所对应的图示强连通的,即图中任何一个节点都可以达到其他任何一个节点,它要求概率转移矩阵不存在某些特殊情况,比如某个列向量都为0,即有一个网页没有链接到任何其他网页,我们把这类情况又称为终止点;或者是在概率转移矩阵的主对角线上,存在有一个元素为1的情况,即这个网页链接只链接它自己,我们把这类情况又称为陷阱。这两类特殊的情形在后面会详细说。 - TT是非周期的。
所谓周期性,体现在Markov链的周期性上。即若A是周期性的,那么这个Markov链的状态就是周期性变化的。因为A是素矩阵(素矩阵指自身的某个次幂为正矩阵的矩阵),所以A是非周期的
比如上面这个例子中,limn→+∞Vn=limn→+∞Tn⋅V0=(3/9,2/9,2/9,2/9)Tlimn→+∞Vn=limn→+∞Tn⋅V0=(3/9,2/9,2/9,2/9)T
这表明,经过足够多次的网页跳转,用户停留在网页A的概率要比停留在B, C, D的概率高,而后三者基本是等概率的。经过这样的计算得到的每个网页的概率值也叫PR值,是评估网页质量的依据。也就是说,在我们使用搜索引擎时,在保持网页与查询一定相关度的基础上,PR值可以提供非常不错的排序依据。
终止点和陷阱
然而,现在存在的问题是,上面的所有推导都是建立在理想状态下的,即假设所有网页组成的这个有向图是强连通的。但是实际上,网页形形色色,总有那么一些“奇葩”存在,从而在PageRank中,对算法会产生“恶劣”影响,基本上有2种情况:终止点和陷阱。
终止点
终止点指的是没有任何出链的网页。可以想象,按照上面这种随机游走模型,用户访问到这个网页后,因为找不到链接,就会“四顾茫然”,不知下一步该怎么办了。比如下图中,网页C没有出链。这种情况下,概率转移矩阵在终止点对应的那一列,所有元素都是0,代入上面的PR值计算公式,会发现经过无穷多次跳转后,所有网页的PR值都是0:
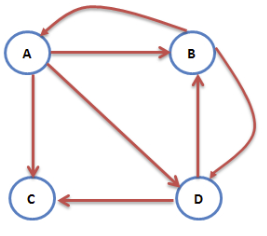
上图对应的概率转移矩阵为:

可见,对应C的第3列全为0,迭代计算PR值,最后的结果都是0:
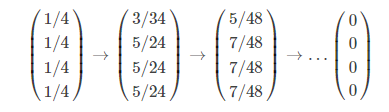
那这样的计算结果当然是毫无意义的。
陷阱
陷阱指的是只有指向自身链接的网页。这种情况下,所有“随机游走”的用户到了这个网页后,就如同进了黑洞一般,一直在里面“打转”,出不来了。比如下图中,网页C只有一条出链,并且还是指向它自己的,这就把C变成了陷阱。
有陷阱的网络对应的概率转移矩阵中,主对角线上存在至少一个为1的元素(主对角线存在nn个1,就代表整个网络中有nn个陷阱)。

T=(01/2001/3001/21/3011/21/31/200)
这种情况下,陷阱的PR值为1,而其他正常网页的PR值为0。迭代计算的结果大致如下:
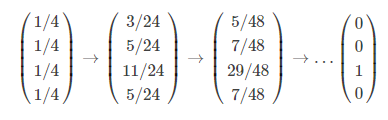
当然,这种结果也是毫无参考意义的。
解决思路
为了解决这两个致命的问题,佩奇和布林想到,他们最初定义的用户的上网模型是不够准确的,因为用户不是傻乎乎的机器,他们是具有聪明大脑的人,当一个人遇到终止点或者陷阱的话,他不会不止所错,也不会无休止地自己打转,他会通过浏览器的地址栏输入新的地址,以逃离这个网页。也就是说,用户从一个网页转至另一个网页的过程中,会以一定的概率不点击当前网页中的链接,而是访问一个自己重新输入的新地址。我们可以依照这个原理修正之前的概率转移公式,如下:
Vn=αTVn−1+(1−α)V0
其中,αα为用户继续点击当前网页中的链接的概率,(1−α)(1−α)为用户通过地址栏“逃离”的概率。关于这里的αα,其实很讲究,首先αα不能太大,因为αα的大小与算法的收敛速度呈反比,
αα太大会导致算法收敛慢而影响性能;其次,αα也不能太小,因为PageRank的精华就在于上面的公式中前一部分——由概率转矩阵的多次迭代计算得到PR值。所以,最终两位博士将αα值定为0.85.
我们来看经过这样处理之后,上面的终止点和陷阱问题能否得到解决:
当存在终止点时,迭代的结果为:
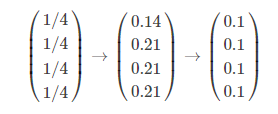
当存在陷阱时,迭代的结果为:
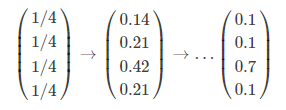
这样就解决了终止点与陷阱的问题。