并查集（Union Find）的基本实现

概念

并查集是一种树形的数据结构，用来处理一些不交集的合并及查询问题。主要有两个操作：

• find：确定元素属于哪一个子集。
• union：将两个子集合并成同一个集合。

所以并查集能够解决网络中节点的连通性问题。

基本实现

package com.yunche.datastructure;

/**
 * @ClassName: UF
 * @Description: 并查集
 * @author: yunche
 * @date: 2018/12/30
 */
public class UF {

    /**
     * 此数组的索引表示节点的编号，数组存储的是对应节点所在的集合编号
     */
    private int[] id;

    /**
     * 节点的个数
     */
    private int count;

    /**
     * 构造函数：构造一个指定大小的并查集
     *
     * @param n 并查集节点的个数
     */
    public UF(int n) {
        id = new int[n];
        count = n;
        for (int i = 0; i < n; i++) {
            id[i] = i;
        }
    }

    /**
     * 查找指定节点的所属的集合编号
     *
     * @param p 节点编号
     * @return 集合编号
     */
    public int find(int p) {
        if (p >= 0 && p < count) {
            return id[p];
        }
        return -1;
    }

    /**
     * 将两个节点所属的集合并在一起，即将两个节点连通
     *
     * @param p 节点编号
     * @param q 节点编号
     */
    public void union(int p, int q) {
        int pId = find(p);
        int qId = find(q);
        if (pId < 0 || qId < 0) {
            return;
        }
        if (qId == pId) {
            return;
        }

        for (int i = 0; i < count; i++) {
            if (id[i] == pId) {
                id[i] = qId;
            }
        }
    }

    /**
     * 判断两个节点是否连通
     * @param p 节点编号
     * @param q 节点编号
     * @return
     */
    public boolean isConnected(int p, int q) {
        return find(p) != -1 && find(p) == find(q);
    }

    /**
     * 测试用例
     * @param args
     */
    public static void main(String[] args) {
        UF uf= new UF(5);
        uf.union(0, 1);
        uf.union(0, 2);
        uf.union(6, 2);
        System.out.println(uf.isConnected(1, 2));
        System.out.println(uf.isConnected(0, 3));
        System.out.println(uf.isConnected(6, 2));
    }
}

对 union 进行 rank 优化

package com.yunche.datastructure;

/**
 * @ClassName: UF2
 * @Description: 针对union进行rank优化
 * @author: yunche
 * @date: 2018/12/30
 */
public class UF2 {

    /**
     * 此数组的索引为节点的编号，数组存储的为对应节点的父节点的编号
     */
    private int[] parent;

    /**
     * 节点的个数
     */
    private int count;

    /**
     * 进一步优化union
     * 数组的索引代表集合的根节点
     * 数组存储的是每个根节点下的对应的树层数
     */
    private int[] rank;


    /**
     * 构造函数：构造一个指定大小的并查集
     *
     * @param n 并查集节点的个数
     */
    public UF2(int n) {
        parent = new int[n];
        rank = new int[n];
        count = n;
        for (int i = 0; i < n; i++) {
            parent[i] = i;
            rank[i] = 1;
        }
    }

    /**
     * 查找指定节点的所属的集合的根节点编号
     *
     * @param p 节点编号
     * @return 根节点编号
     */
    public int find(int p) {
        if (p >= 0 && p < count) {
            while (p != parent[p]) {
                 p = parent[p];
            }
            return p;
        }
        return -1;
    }

    /**
     * 将两个节点所属的集合并在一起，即将两个节点连通
     * 时间复杂度O(n)
     * @param p 节点编号
     * @param q 节点编号
     */
    public void union(int p, int q) {
        int pRoot = find(p);
        int qRoot = find(q);
        if (pRoot < 0 || qRoot < 0) {
            return;
        }
        if (qRoot == pRoot) {
            return;
        }

        //合并两个集合
        //重要优化避免构造树的深度太深
        if (rank[pRoot] < rank[qRoot]) {
            parent[pRoot] = qRoot;
        } else if (rank[pRoot] > rank[qRoot]){
            parent[qRoot] =  pRoot;
        } else {
            parent[pRoot] = qRoot;
            rank[qRoot] += 1;
        }
    }

    /**
     * 判断两个节点是否连通
     * 时间复杂度O(1)
     * @param p 节点编号
     * @param q 节点编号
     * @return
     */
    public boolean isConnected(int p, int q) {
        return find(p) != -1 && find(p) == find(q);
    }

    /**
     * 测试用例
     * @param args
     */
    public static void main(String[] args) {
        testUF2(1000000);
    }

    /**
     * 测试方法
     * @param n 并差集的个数
     */
    public static void testUF2( int n ){

        UF2 uf = new UF2(n);

        long startTime = System.currentTimeMillis();

        // 进行n次操作, 每次随机选择两个元素进行合并操作
        for( int i = 0 ; i < n ; i ++ ){
            int a = (int)(Math.random()*n);
            int b = (int)(Math.random()*n);
            uf.union(a,b);
        }
        // 再进行n次操作, 每次随机选择两个元素, 查询他们是否同属一个集合
        for(int i = 0 ; i < n ; i ++ ){
            int a = (int)(Math.random()*n);
            int b = (int)(Math.random()*n);
            uf.isConnected(a,b);
        }
        long endTime = System.currentTimeMillis();

        // 打印输出对这2n个操作的耗时
        System.out.println("UF2, " + 2*n + " ops, " + (endTime-startTime) + "ms");
    }
}

对 find 进行路径压缩

1、第一种方式

图示

代码

package com.yunche.datastructure;

/**
 * @ClassName: UF3
 * @Description: 对find操作进行路径压缩，第一种路径压缩，过程如图所示
 * @author: yunche
 * @date: 2018/12/30
 */
public class UF3 {

    /**
     * 此数组的索引为节点的编号，数组存储的为对应节点的父节点编号
     */
    private int[] parent;

    /**
     * 节点的个数
     */
    private int count;

    /**
     * 进一步优化union
     * 数组的索引代表集合的根节点
     * 数组存储的是每个根节点下的对应的树深度
     * 在后续的代码中, 我们并不会维护rank的语意, 也就是rank的值在路径压缩的过程中, 有可能不再是树的层数值
     * 这也是我们的rank不叫height或者depth的原因, 它只是作为比较的一个标准
     */
    private int[] rank;


    /**
     * 构造函数：构造一个指定大小的并查集
     *
     * @param n 并查集节点的个数
     */
    public UF3(int n) {
        parent = new int[n];
        rank = new int[n];
        count = n;
        for (int i = 0; i < n; i++) {
            parent[i] = i;
            rank[i] = 1;
        }
    }

    /**
     * 查找指定节点的所属的集合的根节点编号
     * 路径压缩
     * @param p 节点编号
     * @return 根节点编号
     */
    public int find(int p) {
        if (p >= 0 && p < count) {
            while (p != parent[p]) {
                // 根据图示,p的父节点应该指向p的父节点的父节点
                parent[p] = parent[parent[p]];
                //继续从此时p的父节点开始循环
                p = parent[p];
            }
            return p;
        }
        return -1;
    }

    /**
     * 将两个节点所属的集合并在一起，即将两个节点连通
     * 时间复杂度O(n)
     * @param p 节点编号
     * @param q 节点编号
     */
    public void union(int p, int q) {
        int pRoot = find(p);
        int qRoot = find(q);
        if (pRoot < 0 || qRoot < 0) {
            return;
        }
        if (qRoot == pRoot) {
            return;
        }

        //合并两个集合
        //重要优化避免构造树的深度太深
        if (rank[pRoot] < rank[qRoot]) {
            parent[pRoot] = qRoot;
        } else if (rank[pRoot] > rank[qRoot]){
            parent[qRoot] =  pRoot;
        } else {
            parent[pRoot] = qRoot;
            rank[qRoot] += 1;
        }
    }

    /**
     * 判断两个节点是否连通
     * 时间复杂度O(1)
     * @param p 节点编号
     * @param q 节点编号
     * @return
     */
    public boolean isConnected(int p, int q) {
        return find(p) != -1 && find(p) == find(q);
    }

    /**
     * 测试用例
     * @param args
     */
    public static void main(String[] args) {
        UF2.testUF2(1000000);
        testUF3(1000000);
    }/*Output:
    UF2, 2000000 ops, 856ms
    UF3, 2000000 ops, 579ms
     */

    /**
     * 测试方法
     * @param n 并查集的个数
     */
    public static void testUF3( int n ){

        UF3 uf = new UF3(n);

        long startTime = System.currentTimeMillis();

        // 进行n次操作, 每次随机选择两个元素进行合并操作
        for( int i = 0 ; i < n ; i ++ ){
            int a = (int)(Math.random()*n);
            int b = (int)(Math.random()*n);
            uf.union(a,b);
        }
        // 再进行n次操作, 每次随机选择两个元素, 查询他们是否同属一个集合
        for(int i = 0 ; i < n ; i ++ ){
            int a = (int)(Math.random()*n);
            int b = (int)(Math.random()*n);
            uf.isConnected(a,b);
        }
        long endTime = System.currentTimeMillis();

        // 打印输出对这2n个操作的耗时
        System.out.println("UF3, " + 2*n + " ops, " + (endTime-startTime) + "ms");
    }
}

2、第二种方式

在明白了第一种压缩路径的方法后，我们可能会疑惑：是否这就是最短的路径了？我们仔细思考后会发现，这并不是最短的路径，最短的路径形成的树应该只有2层，第一层为根节点，其余所有节点都在第二层指向根节点，如下图所示。要实现这种压缩路径的方式也简单，使用递归即可。

图示

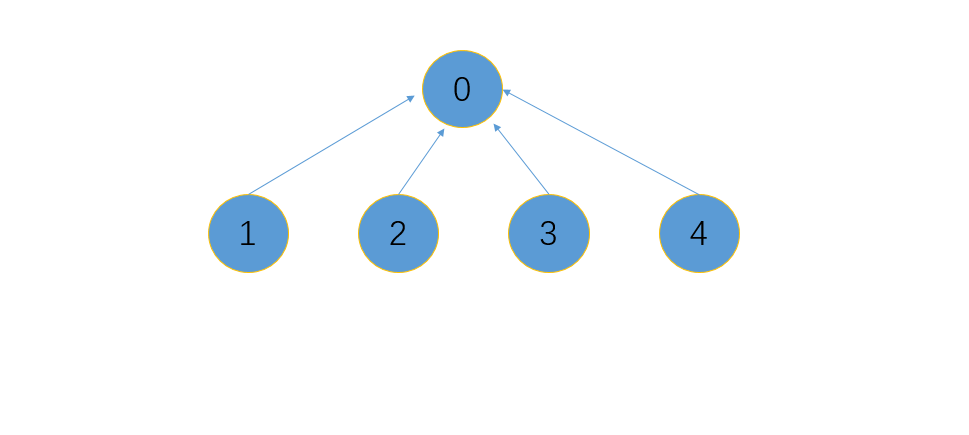
代码

package com.yunche.datastructure;

/**
 * @ClassName: UF4
 * @Description: 对find操作进行路径压缩，第二种路径的递归压缩
 * @author: yunche
 * @date: 2018/12/30
 */
public class UF4 {

    /**
     * 此数组的索引为节点的编号，数组存储的为对应节点的父节点编号
     */
    private int[] parent;

    /**
     * 节点的个数
     */
    private int count;

    /**
     * 进一步优化union
     * 数组的索引代表集合的根节点
     * 数组存储的是每个根节点下的对应的树层数
     * 在后续的代码中, 我们并不会维护rank的语意, 也就是rank的值在路径压缩的过程中, 有可能不再是树的层数值
     * 这也是我们的rank不叫height或者depth的原因, 它只是作为比较的一个标准
     */
    private int[] rank;


    /**
     * 构造函数：构造一个指定大小的并查集
     *
     * @param n 并查集节点的个数
     */
    public UF4(int n) {
        parent = new int[n];
        rank = new int[n];
        count = n;
        for (int i = 0; i < n; i++) {
            parent[i] = i;
            rank[i] = 1;
        }
    }


    /**
     * 压缩路径递归实现 递归算法
     * @param p 节点编号
     * @return 返回节点当前的根节点编号
     */
    public int find(int p) {
        if (p >= 0 && p < count) {
            // 递归边界
            if (p == parent[p]) {
                return p;
            }
            //想象此时有 3 层：分别是 0, 1, 2,最开始p = 2
            // 那么第一次执行到这个位置 parent[2] = findRecursive(1)
            //第二次执行到这个位置 parent[1] = findRecursive(0)
            //当再一次递归此时，到不到这一步，因为触发递归边界，返回0
            //那么，向上 parent[1] = 0
            //再向上，parent[2] = parent[1] = 0
            parent[p] = find(parent[p]);
            return parent[p];
        }
        return -1;
    }

    /**
     * 将两个节点所属的集合并在一起，即将两个节点连通
     * 时间复杂度O(n)
     * @param p 节点编号
     * @param q 节点编号
     */
    public void union(int p, int q) {
        int pRoot = find(p);
        int qRoot = find(q);
        if (pRoot < 0 || qRoot < 0) {
            return;
        }
        if (qRoot == pRoot) {
            return;
        }

        //合并两个集合
        //重要优化避免构造树的深度太深
        if (rank[pRoot] < rank[qRoot]) {
            parent[pRoot] = qRoot;
        } else if (rank[pRoot] > rank[qRoot]){
            parent[qRoot] =  pRoot;
        } else {
            parent[pRoot] = qRoot;
            rank[qRoot] += 1;
        }
    }

    /**
     * 判断两个节点是否连通
     * 时间复杂度O(1)
     * @param p 节点编号
     * @param q 节点编号
     * @return
     */
    public boolean isConnected(int p, int q) {
        return find(p) != -1 && find(p) == find(q);
    }

    /**
     * 测试用例
     * @param args
     */
    public static void main(String[] args) {
        UF2.testUF2(1000000);
        UF3.testUF3(1000000);
        UF4.testUF4(1000000);
    }/*Output:
   UF2, 2000000 ops, 918ms
   UF3, 2000000 ops, 586ms
   UF4, 2000000 ops, 631ms
     */

    /**
     * 测试方法 -
     * @param n 并查集的个数
     */
    public static void testUF4( int n ){

        UF4 uf = new UF4(n);

        long startTime = System.currentTimeMillis();

        // 进行n次操作, 每次随机选择两个元素进行合并操作
        for( int i = 0 ; i < n ; i ++ ){
            int a = (int)(Math.random()*n);
            int b = (int)(Math.random()*n);
            uf.union(a,b);
        }
        // 再进行n次操作, 每次随机选择两个元素, 查询他们是否同属一个集合
        for(int i = 0 ; i < n ; i ++ ){
            int a = (int)(Math.random()*n);
            int b = (int)(Math.random()*n);
            uf.isConnected(a,b);
        }
        long endTime = System.currentTimeMillis();

        // 打印输出对这2n个操作的耗时
        System.out.println("UF4, " + 2*n + " ops, " + (endTime-startTime) + "ms");
    }


}

3、 两种压缩路径的比较

从理论上说，第二种压缩路径算法应该比第一种快，但上面的测试方法的结果却是第一种压缩路径算法更快，这是因为第二种压缩算法有递归上的开销，结果上也表面这两种算法效率是差别不大的，所以采取哪种方法要实际测试下。