NLP --- 文本分类（基于概率的隐语意分析（PLSA）详解）

上一节我们详细的讲解了SVD的隐语意分析，一旦提到这个，大家脑海里应该立刻有如下的矩阵形式：

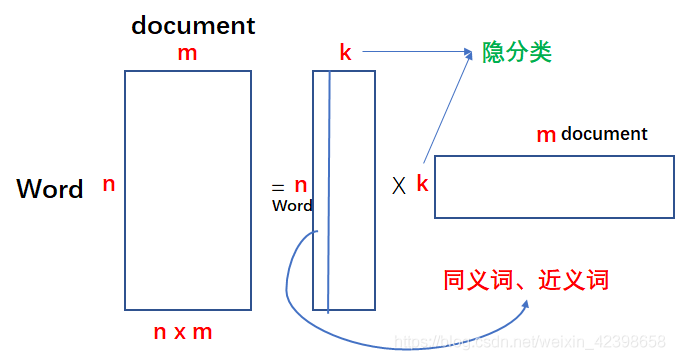
我们通过矩阵的分解对文本数据进行压缩，压缩量很可观，尤其是原始的矩阵的维度很高时压缩的更可观，因为k通常要远远小于n。如上图等号左边的矩阵其实就是我们的文本的词向量组成的，我们知道一篇文章的词是很多的，而且还是稀疏的，如果一旦文章数也很多,那么整个矩阵的元素会很大很大，但是通过矩阵分解就会减少很多。上图中的每一列都代表一个文本的词向量，里面的值是词向量的权值，那么我们分解后的矩阵分别代表什么呢？其中k就是隐分类或者说是隐特征，如果多个词在同一列出现就说明这几个词是相近的，在最右边的矩阵是什么意思呢？可以理解为经过压缩后的文本特征，每个文本都有k个特征，然后对比一下，以此来判断是否相似。还有一种用法就是我先通过矩阵分解，然后在组合成nxm的矩阵，这个新组合的矩阵和原始矩阵很像，但是肯定不一样，因为我们中间在特征值时略去了部分特征值，怎么理解这一步呢？大家可以理解为我们是去除噪声，留下的才是主要特征，和PCA技术差不多。但是这个方法就没有缺点吗？有的，下面我们来看看：

缺点是SVD的分解的计算量太大，计算复杂度高，当矩阵达到1000维以上时计算已经非常缓慢，但文本分析一般都会形成非常大型的“文档-词”矩阵，从而难以实现，甚至存储都很困难。因此需要引入新的求解SVD的方法，这时一种新型的求解思路就出来了，下面还以推荐系统的电影分类为例进行讲解：

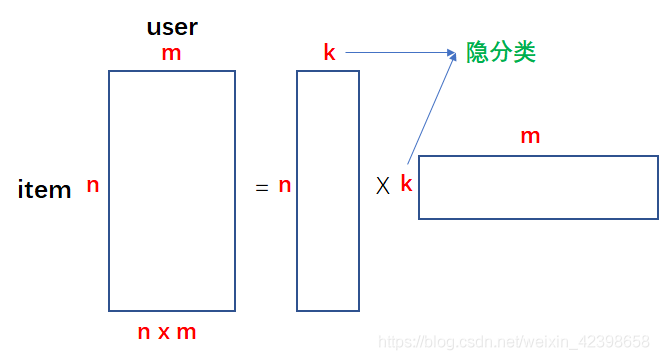
按照我们上一节的内容就是当得到评分矩阵时，就可以直接对其进行分解，但是问题是当这个评分矩阵的维度很大时，SVD的计算量将很大，为了避免这么大的计算量，我们采用这样的做法，就是我把上图的等号右边的两个矩阵的元素全看做变量，对，你没看错，全看做变量，那么我让他们相乘就会得到和原始评分矩阵维度一样的矩阵，那么这个时候我把原始矩阵已知的值和计算出来的矩阵相对应位置的值尽量相等，这样就建立了优化函数，然后使用优化算法使其误差达到最低，一旦我们合成的矩阵符合我们的要求，同时就可推测原始评分稀疏矩阵的值了，通过预测的值的大小就可以推荐给用户分值高的电影了，下面结合图来讲：

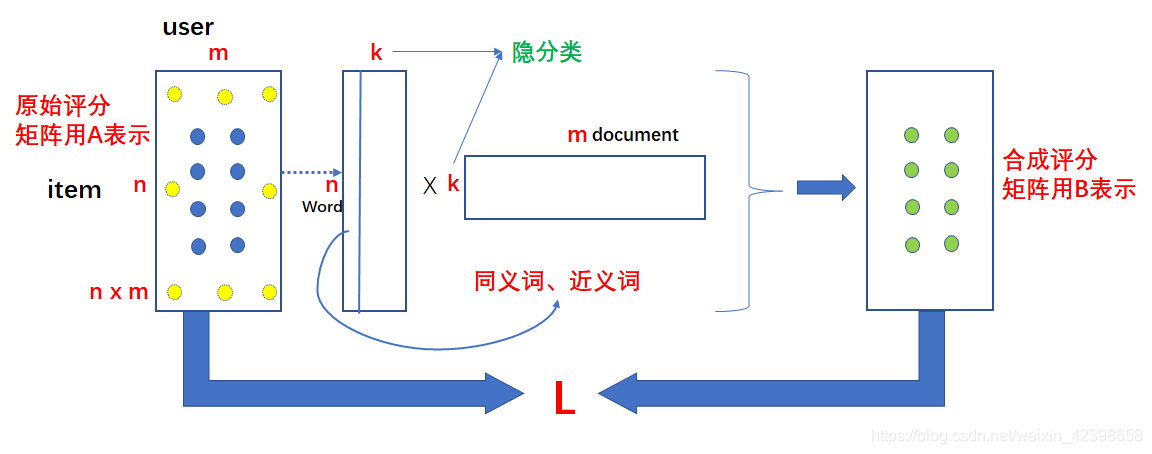
首先我们构建两个矩阵维度为nxk和kxm的，如上图的中间部分，那么我把这两个矩阵的元素都看做变量，这时候把矩阵相乘得到合成评分矩阵B，如上图的右端，那么把合成的数据和原始的评分矩阵A对应的位置相比较如上图的A蓝色点，黄色点是缺少的（意思是用户没有看过该影片），使他们尽量的接近，怎么衡量呢？误差平方和函数呀，因此可以得到关于很多变量的误差函数L，此时我们使用优化算法进行优化，一旦达到我们的要求，那么说明我们的分解矩阵就确定了，此时使用这个再去预测A矩阵的位置的黄色的点，这可以对评分矩阵的稀缺值进行填充，进而根据分值大小给用户推荐电影了，就是这个原理。这样就巧妙的避免了求解SVD了，一旦得到优化函数，我们就可以通过梯度下降得到我们的极值，下面我们就介绍一下基于PLSA对文本分类的算法。

基于PLSA对文本分类

尽管基于 SVD 的 LSA 取得了一定的成功，但是其缺乏严谨的数理统计基础，而且 SVD 分解非常耗时。Hofmann 在 SIGIR'99 上提出了基于概率统计的 PLSA 模型，并且用 EM 算法学习模型参数。PLSA 的概率图模型如下：

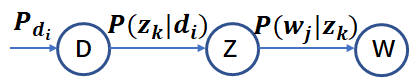
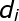
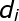
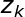
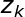
其中 D 代表文档，Z 代表隐含类别或者主题，W 为观察到的单词，表示单词出现在文档 $\large d_i$ 的概率，表示文档 $\large d_i$ 中出现主题 $\large z_k$ 下的单词的概率，给定主题 $\large z_k$ 出现单词 $\large w_j$ 的概率。并且每个主题在所有词项上服从Multinomial 分布，每个文档在所有主题上服从Multinomial 分布。整个文档的生成过程是这样的：

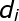
(1) 以的概率选中文档 $\large d_i$ ；
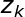
(2) 以的概率选中主题 $\large z_k$ ；
(3) 以的概率产生一个单词。
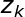
我们可以观察到的数据就是 $\large (d_i,w_j)$ 对，而 $\large z_k$ 是隐含变量。 $\large (d_i,w_j)$ 的联合分布为:

而和分别对应了两组 Multinomial 分布，我们需要估计这两组分布的参数。

这里需要好好解释一下，其中 $\large P(d_i,w_j)$ 就是我们上面的推荐系统的A评分矩阵，就是我们的上面分解第一个矩阵，而 $\large P(z_k|d_i)$ 就是我们分解的第二个矩阵，这里大家把这些矩阵里的数全看成概率理解就容易了。因此上式其实就是我们上面SVD分解的概率形式而已，这里在把公式写一下：

$\large P(d_i,w_j)=P(d_i)\sum_{k=1}^{K}P(w_j|z_k)P(z_k|d_i)$

其中 $\large P(d_i)$ 大家把他看成概率归一化因子就好了。现在如何求，因为 $\large w_j,z_k,d_i$ 都是未知的，怎么求呢？这里可以通过EM算法进行求解，这里需要大家理解EM算法，不理解的请参考我的这篇文章。

用EM估计PLSA中的参数

首先我们根据最大释然估计写出释然函数，如下：

其中 $\large n(d_i,w_j)$ 是单词 $\large w_j$ 出现在文档 $\large d_i$ 中的次数。注意这是一个关于和 $\large P(z_k|d_i)$ 的函数，一共有 N*K + M*K 个自变量，如果直接对这些自变量求偏导数，我们会发现由于自变量包含在对数和中，这个方程的求解很困难。因此对于这样的包含“隐含变量”或者“缺失数据”的概率模型参数估计问题，我们采用 EM 算法。

EM 算法的步骤是：
(1)E 步骤：求隐含变量 Given 当前估计的参数条件下的后验概率。
(2)M 步骤：最大化 Complete data 对数似然函数的期望，此时我们使用 E 步骤里计算的隐含变量
的后验概率，得到新的参数值。
两步迭代进行直到收敛。

针对我们 PLSA 参数估计问题，在 E 步骤中，直接使用贝叶斯公式计算隐含变量在当前参数取值条件下的后验概率，有

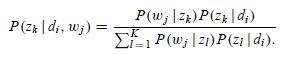
在这个步骤中，我们假定所有的和 $\large P(z_k|d_i)$ 都是已知的，因为初始时随机赋值，后面迭代的过程中取前一轮 M 步骤中得到的参数值。

在 M 步骤中，我们最大化 Complete data 对数似然函数的期望。在 PLSA 中，Incomplete data 是观察到的 $\large (d_i,w_j)$ ，隐含变量是主题 $\large z_k$ ，那么 complete data 就是三元组 $\large (d_i,w_j,z_k)$ ，其期望是:

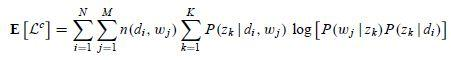
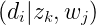
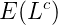
注意这里 $\large (d_i|z_k,w_j)$ 是已知的，取得是前面 E 步骤里面的估计值。下面我们来最大化期望，这又是一个多元函数求极值的问题，可以用拉格朗日乘数法。拉格朗日乘数法可以把条件极值问题转化为无条件极值问题，在 PLSA 中目标函数就是 $\large E(L^c)$ ,约束条件是

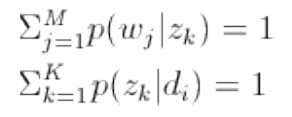
由此我们可以写出拉格朗日函数

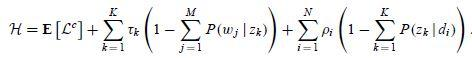
这是一个关于和 $\large P(z_k|d_i)$ 的函数，分别对其求偏导数，我们可以得到

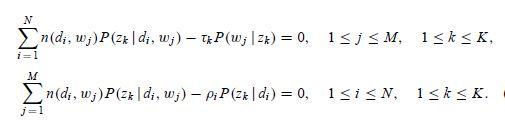
注意这里进行过方程两边同时乘以和 $\large P(z_k|d_i)$ 的变形，联立上面 4 组方程，我们就可以解出 M 步骤中通过最大化期望估计出的新的参数值

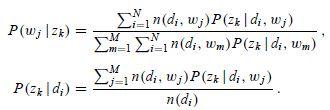
解方程组的关键在于先求出 $\large \tau _k,\rho _j$ ,其实只需要做一个加和运算就可以把 $\large \tau _k,\rho _j$ 的系数都化成 1，后面就好计算了。然后使用更新后的参数值，我们又进入 E 步骤，计算隐含变量 $\large z_k$ Given 当前估计的参数条件下的后验概率。如此不断迭代，直到满足终止条件。

本节主要参考了：

概率语言模型及其变形系列PLSA 及及 EM 算法 [email protected] 12/20/2012