稀疏化邻近度图

第三十三次写博客，本人数学基础不是太好，如果有幸能得到读者指正，感激不尽，希望能借此机会向大家学习。本文作为基于图的聚类的第一部分，主要针对“如何稀疏化邻近度图”以及“如何在稀疏化后的邻近度图上运行聚类算法”，本文还会针对数据结构与算法中的两种构建“最小生成树（Minimum Spanning Tree）”的算法（Prim和Kruskal）进行介绍。其他基于图的聚类算法的链接可以在这篇综述《基于图的聚类算法综述（基于图的聚类算法开篇）》的结尾找到。

如何进行稀疏化

$m$ 个数据点的 $m\times{m}$ 邻近度矩阵可以用一个稠密图表示，图中每个结点与其他所有结点相连接，任意一对结点之间边的权值反映他们之间的邻近性。尽管每个对象与其他每个对象都有某种程度的邻近性，但是对于大部分数据集，对象只与少量对象高度相似，而与大部分其他对象的相似性很弱。这一性质可以用来稀疏化邻近度图（矩阵）：在实际的聚类过程开始之前，将许多地相似度（高相异度）的值置零。例如，稀疏化可以这样进行：断开相似度（相异度）低于（高于）制定阈值的边，或仅保留连接到点的 $k$ 个最近邻的边。后一种方法创建所谓“ $k$ -最近邻图”（K-nearest Neighbor Graph）。
稀疏化的优点体现在以下几方面：
(1) 压缩了数据量:聚类所需要处理的数据被大幅度压缩，稀疏化常常可以删除邻近度矩阵中99%以上的像，这样，可以处理的问题的规模就提高了。
(2) 可以更好的聚类:稀疏化技术保持了对象与最近邻的连接，而断开了与较远对象的连接，这与最近邻原理一致：对象的最近邻趋向于与对象在同一个类（簇）。优点是降低了噪声与离群点的影响，增强了簇之间的差别。
(3)可以使用图划分算法:下面介绍的两种算法MST和OPOSSUM都使用了图划分。
应当把邻近度图的稀疏化看成使用实际聚类算法之前的初始化步骤。理论上讲，完美的稀疏化应当将邻近度图划分成对应于期望簇的连通分支。但实际中这很难做到，很容易出现单边连接两个簇，或者单个簇被分裂成若干个不相连接的子簇的情况，因此需要常常修改稀疏邻近度图，以便产生新的邻近度图，新的邻近度图还可以被稀疏化，聚类算法使用的邻近度图是所有这些预处理步骤的结果，如下图所示。

图1 使用稀疏化聚类的理想过程

MST聚类

1. MST（Minimum Spanning Tree）
这一部分介绍“最小生成树”（Minimum Spanning Tree，简称MST），一个无向图 $G$ 的最小生成树就是由该图的那些连接 $G$ 的所有顶点的边构成的树，且其总价值最低，在MST中，顶点和边的总数量分别为 $|V|$ 和 $|V|-1$ （如图2所示）。当然也可以为有向图生成MST，但是过程更复杂，由于算法的需要这里只介绍无向图构建MST，下面介绍两种构建算法：Prim和Kruskal，他们的区别在于如何选取最小（值的）边。

图2 无向图和最小生成树

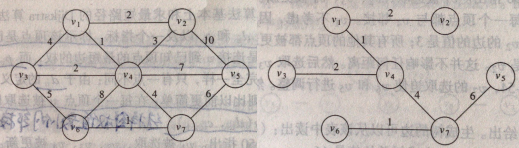
1) Prim算法
Prim计算最小生成树的方法是使其连续的一步步长成，在每一部，都要把每个结点作为根并向其加边，即每一步加入一条边和一个顶点。具体的步骤是，首先从 $G$ 中随机选择一个结点加入到树中，然后每一步通过选择边 $\left(u,v\right)$ ，使得 $\left(u,v\right)$ 的值是所有 $u$ 在树上但 $v$ 不在树上的边的值中的最小者，而找出一个新的结点并把他加入到这棵树中。图3是使用Prim完成图2所示MST的生成步骤，具体内容见《数据结构与算法分析》P237。

图3 Prim算法

2) Kruskal算法
这种算法连续的按照最小的权选择边 $\left(u,v\right)$ ，并且当所选的边不产生圈时就把他作为确定的边添加到树中，当添加的边足够多时就停止算法。实际上算法要决定的就是是否要添加当前选择的边 $\left(u,v\right)$ ，如果顶点 $u$ 、 $v$ 均存在于树的顶点集合中，那么就放弃，否则添加这条边。图4和图5是使用Kruskal完成图2所示MST的生成步骤，具体内容见《数据结构与算法分析》P239。

图4 Kruskal算法

图5 Kruskal算法

2. MST算法
MST算法可以看做是一种分裂层次聚类算法，实际上他产生的聚类模型与使用单链的凝聚层次聚类相同，MST算法的第一步是找到原邻近度图的最小生成树，最小生成树也可以看做是一种稀疏化的邻近度图，然后每次断开树中最大相异度的边，直到达到期望的簇数量，算法伪代码如下图所示。

图6 MST算法伪代码

OPOSSUM聚类

Opossum (Optimal Partitioning of Sparse Similarities Using Metis) 是一种使用METIS算法（可以采用现有的计算包，见《Multilevel k -way Partitioning Schemefor Irregular Graphs》）的稀疏邻近度图的最优划分算法，它基于一些适用于“购物篮数据”的约束，对稀疏化后的邻近度图进行划分。需要注意的是，这里的相似度度量应该采用某些适用于高维、稀疏数据的度量，如余弦度量和Jaccard度量等。该算法期望得到对于进一步分析同等重要的簇，因此，OPOSSUM算法遵循以下两条约束（如图7和图8所示）来得到平衡的簇集合：
1) 采样平衡
每个簇应该大致上包含同等大小的样本点数，即 $n/k$ ，这有助于零售商得到相同大小的顾客群组来进行市场分析。

图7 约束一

2) 值平衡
每个簇中样本点的属性值总和应该大致相等，这样每个簇代表全部特征值总和的 $1/k$ ，如果我们使用扩展的单一商品的收入（数量x单价）作为属性值的度量方法，那么每个簇对总商品收入的贡献大致相等。

图8 约束二

该算法通过为每个样本点（顾客）赋予一个权重并对一个簇中所有样本点权值的总和稍加限制，来满足上述约束。对于采样平衡情况，我们为每个样本点 $\mathbf{x}_j$ 赋予相等的权值 $w_j=1$ ，对于值平衡情况，每个样本点的权值与他属性值的总和有关，可以表示为 $w_j=\sum^{d}_{i=1}x_{i,j}$ 。
该算法的优点是简单、快速的得到大小近似相等的簇，缺点也显而易见，由于产生的簇大小相同，因此会导致期望簇被不合理的分裂或合并，因此一般采用过度聚类（Over-Clustering，设置较大的 $k$ 值）随后进行簇合并。

参考资料

【1】《数据挖掘导论》
【2】《数据结构与算法》
【3】 Karypis G , Kumar V . Multilevelk-way Partitioning Scheme for Irregular Graphs[M]. Academic Press, Inc. 1998.
【4】 Strehl A , Ghosh J . A Scalable Approach to Balanced, High-Dimensional Clustering of Market-Baskets.[C]// International Conference on High Performance Computing. Springer-Verlag, 2000.