上篇文章我们已经学习了循环神经网络的原理,并指出RNN存在严重的梯度爆炸和梯度消失问题,因此很难处理长序列的数据。本篇文章,我们将学习长短期记忆网络(LSTM,Long Short Term Memory),看LSTM解决RNN所带来的梯度消失和梯度爆炸问题。
1.从RNN到LSTM
RNN模型具有如下所示的结构,其中每个索引位置t都有一个隐藏状态
h(t)。
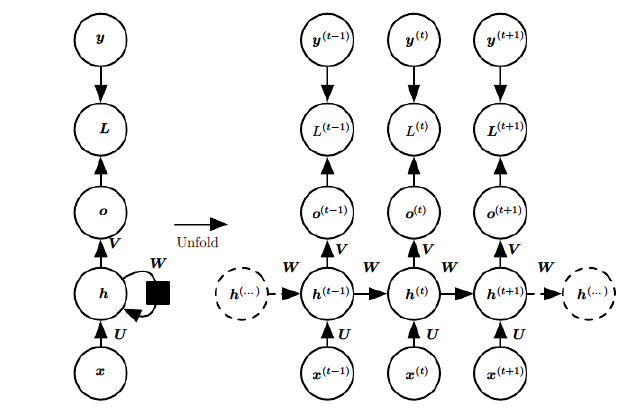
如果省略每层的
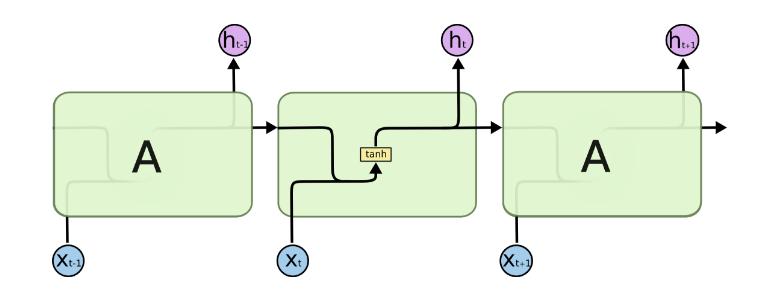
o(t),L(t),y(t),则RNN模型可以简化到如下所示的结构。其中隐藏状态的
h(t)由
x(t)和
h(t−1)得到,得到
h(t)后可用于计算当前层的模型损失和下一层的
h(t+1)。
为解决梯度消失的问题,大牛们针对RNN序列索引位置t的隐藏结构作出相应改进,进而提出LSTM模型。其中LSTM模型有多种形式,下面我们以最常见的LSTM模型为例进行讲解。
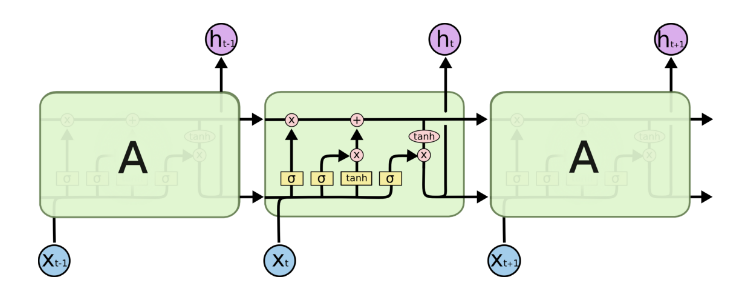
2.LSTM模型结构
LSTM模型除了和RNN模型具有相同的隐藏状态
h(t)外,还增加了新的隐藏状态
C(t),如下图中横线所示。新增加的隐藏状态称为细胞状态(Cell State),记为
C(t)。
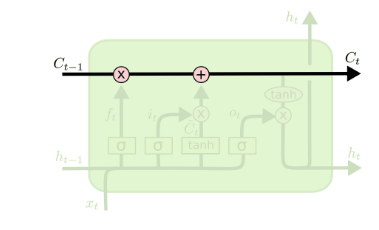
除了细胞状态外,LSTM中还多了很多奇怪的结构,称之为门控结构(Gate)。针对每个序列索引位置t,门控结构一般包含遗忘门、输入门和输出门,下面来看看门控结构和细胞状态的结构。
2.1 LSTM之遗忘门
**遗忘门(forget gate)**是以一定的概率控制是否遗忘上一层的隐藏细胞状态,遗忘门的结构如下所示。
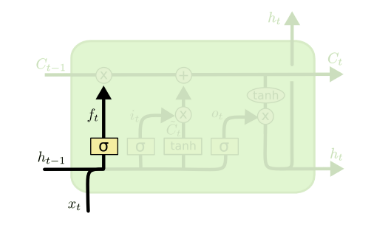
输入是上一序列的隐藏状态
h(t−1)和本序列数据
x(t),通过一个激活函数(一般是sigmoid),得到遗忘门的输出
f(t)。由于sigmoid的输出
f(t)在[0,1]之间,因此这里的
f(t)代表遗忘上一层隐藏细胞状态的概率,数学表达式如下所示。其中
Wf,Uf,bf为线性关系的系数和偏倚,
σ为sigmoid激活函数。
f(t)=σ(Wfh(t−1)+Ufx(t)+bf)
2.2 LSTM之输入门
**输入门(input gate)**负责处理当前序列位置的输入,输入门的结构如下所示。
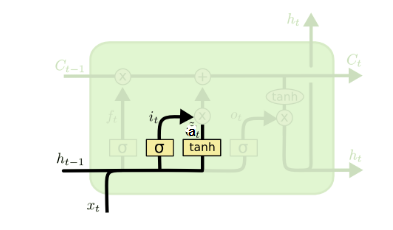
输入门由两部分组成,第一部分使用sigmoid激活函数,输出为
i(t),第二部分使用tanh激活函数,输出为
a(t),两者的结果后面会用于相乘后更新细胞状态。
i(t)和
a(t)数学表达式如下所示,其中
Wi,Ui,bi,Wa,Ua,ba为线性关系的系数和偏倚,
σ为sigmoid激活函数。
i(t)=σ(Wih(t−1)+Uix(t)+bi)
a(t)=tanh(Wah(t−1)+Uax(t)+ba)
2.3 LSTM之细胞状态更新
研究LSTM输出门之前,我们先看一下LSTM细胞状态的更新,其中遗忘门和输入门的结果都作用于细胞状态
C(t)。
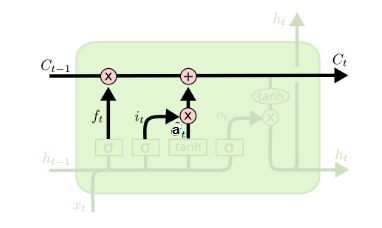
细胞状态
C(t)由两部分组成,第一部分是
C(t−1)和遗忘门输出
f(x)的乘积,第二部分是输入门的
i(t)和
a(t)的乘积,公式如下所示,其中
⊙为Hadamard积。
C(t)=C(t−1)⊙f(t)+i(t)⊙a(t)
2.4 LSTM之输出门
有了新的隐藏细胞状态
C(t),便可以来看输出门,其结构如下所示。
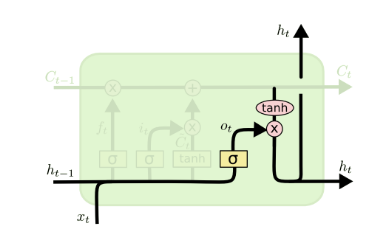
隐藏状态
h(t)的细胞状态由两部分组成,第一部分
o(t)由上一序列的隐藏状态
h(t−1)和本序列数据
x(t),以及激活函数Sigmoid组成。第二部分由隐藏状态
C(t)和tanh激活函数组成,公式如下所示
o(t)=σ(Woh(t−1)+Uox(t)+bo)
h(t)=o(t)⊙tanh(Ct)
3.LSTM之前向传播算法
通过上面的介绍,已经能够得到LSTM前向传播算法主要包括更新遗忘门输出、更新输入门、更新细胞状态、更新输出门、更新当前序列索引预测输出,各传播过程如下所示。
f(t)=σ(Wfh(t−1)+Ufx(t)+bf)
i(t)=σ(Wih(t−1)+Uix(t)+bi)
a(t)=tanh(Wah(t−1)+Uax(t)+ba)
C(t)=C(t−1)⊙f(t)+i(t)⊙a(t)
o(t)=σ(Woh(t−1)+Uox(t)+bo)
h(t)=o(t)⊙tanh(C(t))
y^(t)=σ(Vh(t)+c)
4.LSTM之反向传播算法
了解前向传播算法流程之后,对于反向传播算法就非常简单了。我们采用和RNN相同的反向传播算法思路,即通过梯度下降法迭代更新所有的参数。
RNN之中,我们通过隐藏状态
h(t)和梯度
δ(t)来反向传播误差。在LSTM中,我们有两个隐藏状态,即
h(t)和
C(t)
δh(t)=∂h(t)∂L
δC(t)=∂C(t)∂L
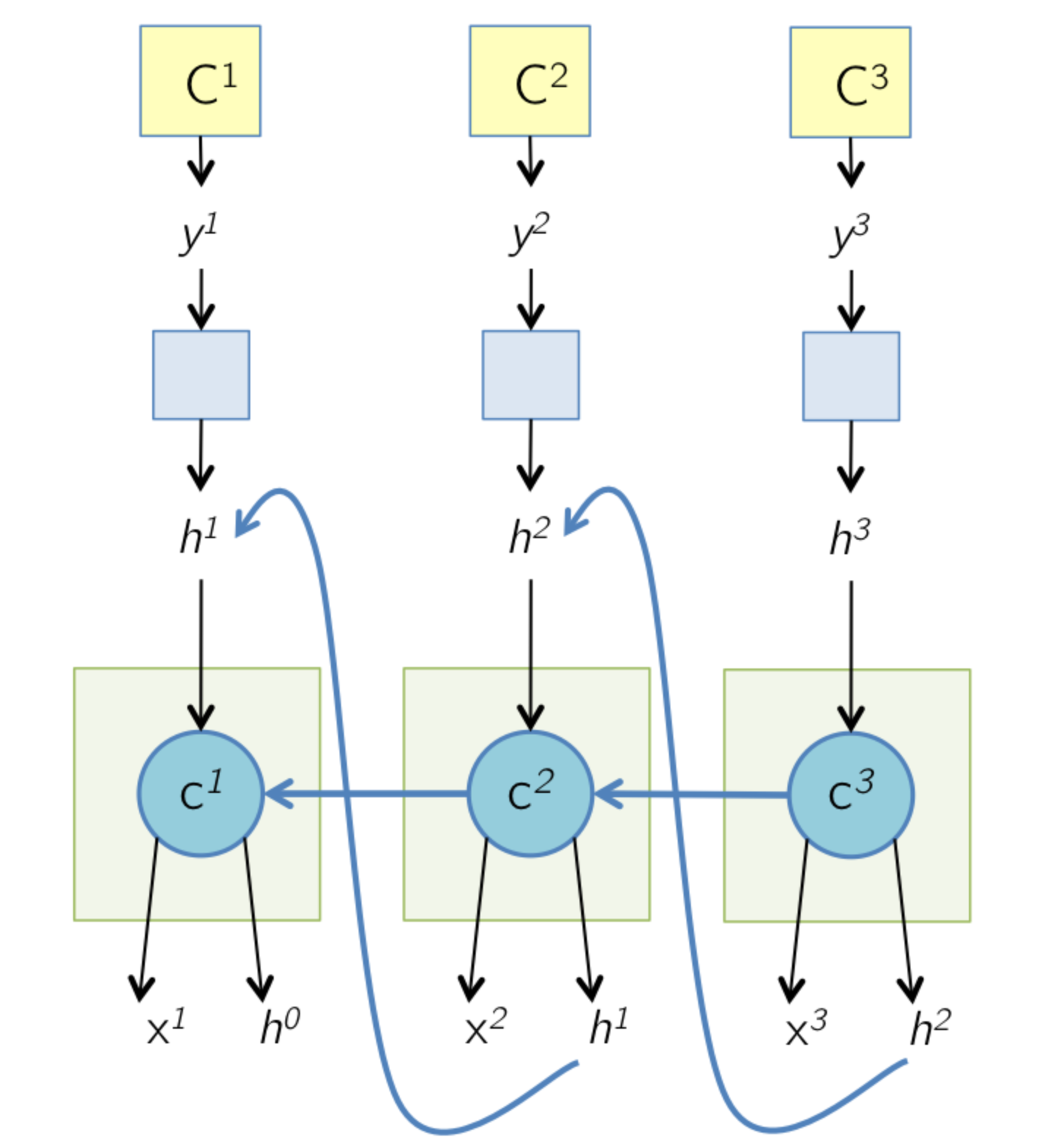
反向传播时,只有
δC(t)在反向传播,
δh(t)帮助在当前层计算,如下图所示。
现在我们便来推导反向传播公式,首先是在最后索引位置
τ的
δh(τ)和
δC(τ)
δh(τ)=∂O(τ)∂L∂h(τ)∂O(τ)=VT(y^(τ)−y(τ))
δC(τ)=∂h(τ)∂L∂C(τ)∂h(τ)=δh(τ)⊙o(τ)⊙(1−tanh2(C(τ)))
接着由
δC(t+1)反向推导
δC(t),其中
δh(t)的梯度由本层的输出梯度误差决定,即
δh(t)=∂h(t)∂L=VT(y^(τ)−y(τ))
而
δC(t)的反向梯度由上一层
δC(t+1)的梯度误差和本层从
h(t)传回来的梯度误差两部分决定,即
δC(t)=∂C(t+1)∂L∂C(t)∂C(t+1)+∂h(t)∂L∂C(t)∂h(t)=δC(t+1)⊙f(t+1)+δh(t)⊙o(t)⊙(1−tanh2(C(t)))
有了
δh(t)和
δC(t)之后,计算
Wf,Uf,bf,Wa,Ua,ba,Wi,Ui,bi,Wo,Uo,bo,V,c的梯度也就相对很容易了,比如
Wf为
∂Wf∂L=t=1∑τ∂C(t)∂L∂f(t)∂C(t)∂Wf∂f(t)=t=1∑τδC(t)⊙C(t−1)⊙f(t)⊙(1−f(t))(h(t−1))T
5.LSTM怎么解决梯度消失和梯度爆炸
RNN反向传播过程中我们得到如下公式。因为${\tanh}’ \leq 1 $,对于训练过程中大部分情况tanh的导数是小于1的,如果W也是大于0小于1的值,那么传播下去便会趋于0,同理当W很大时,传播下去便会趋于无穷。因此便会出现梯度消失和梯度爆炸的问题。
∂h(t)∂h(t+1)=diag(1−(h(t+1))2)WT
LSTM能够很好的解决梯度消失和梯度爆炸问题,但怎么解决的呢。我们来看看反向传播过程中
Wf的变化
∂Wf∂L=t=1∑τ∂C(t)∂L∂f(t)∂C(t)∂Wf∂f(t)=t=1∑τ∂C(t+1)∂L∂C(t)∂C(t+1)∂f(t)∂C(t)∂Wf∂f(t)=t=1∑τ(∂C(t)∂C(t+1))δC(t+1)⊙C(t−1)⊙f(t)⊙(1−f(t))(h(t−1))T
因为
C(t)=C(t−1)⊙f(t)+i(t)⊙a(t),所以
∂C(t)∂C(t+1)为
∂C(t)∂C(t+1)=(f(t+1)+...)
公式里其余项不重要,这里用省略号代替。可以看出当
f(t+1)=1时,就算其余项很小,梯度仍然可以很好地传导到上一个时刻,即使层数较深也不会发生梯度下降的问题。当
f(t+1)=0时,上一时刻的信号不影响到当前时刻,则此项也会为0,
f(t)在这里控制着梯度传导到上一时刻的衰减程度。
5.LSTM总结
LSTM虽然复杂,但能够很好的解决梯度消失和梯度爆炸的问题,只要我们理清各部分之间的关系,进而理解前向和反向传播算法还是不难的。针对RNN和LSTM之中的梯度消失和梯度爆炸的描述,如果有相应错误,欢迎指出。
6.推广
更多内容请关注公众号谓之小一,若有疑问可在公众号后台提问,随时回答,欢迎关注,内容转载请注明出处。










